Chances Are (7 page)
Authors: Michael Kaplan

3
Elaborating
The same arguments which explode the Notion of Luck may, on the other
side, be useful in some Cases to establish a due comparison between
Chance and Design. We may imagine Chance and Design to be as it were
in Competition with each other for the production of some sorts of Events,
and may calculate what Probability there is, that those Events should be
rather owing to one than to the other.
side, be useful in some Cases to establish a due comparison between
Chance and Design. We may imagine Chance and Design to be as it were
in Competition with each other for the production of some sorts of Events,
and may calculate what Probability there is, that those Events should be
rather owing to one than to the other.
âAbraham de Moivre,
Doctrine of Chances
Doctrine of Chances
Â
Â
Â
Â
Â
Â
N
ewton, apparently, would fob off students who pestered him with mathematical questions by saying, “Go to Mr. de Moivre; he understands these things better than I do.” Abraham de Moivre was a Huguenot refugee who had arrived in London in 1688 with no other patrimony than a Sorbonne education in mechanics, perspective, and spherical trigonometry. It was both more than enough and not nearly enough; for 66 years he didn't quite make ends meetâpublishing this and that, tutoring the sons of earls, helping insurance agents calculate mortality, and selling advice to gamblers on the odds.
ewton, apparently, would fob off students who pestered him with mathematical questions by saying, “Go to Mr. de Moivre; he understands these things better than I do.” Abraham de Moivre was a Huguenot refugee who had arrived in London in 1688 with no other patrimony than a Sorbonne education in mechanics, perspective, and spherical trigonometry. It was both more than enough and not nearly enough; for 66 years he didn't quite make ends meetâpublishing this and that, tutoring the sons of earls, helping insurance agents calculate mortality, and selling advice to gamblers on the odds.
De Moivre's new technique for calculating odds was algebra: consider how powerfully it deals with de Méré's first problemâhow many throws of two dice you need to have an even chance of throwing a double-six. This being algebra, he does not start with one trial and then scale up, he boldly puts an
x
where we expect to find our answer and takes the most general form of the problem: if something happens
a
times or does not happen
b
times during
x
trials, then we can say, putting the power law into general terms, that the chance of its not happening in
every
trial is:
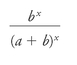
x
where we expect to find our answer and takes the most general form of the problem: if something happens
a
times or does not happen
b
times during
x
trials, then we can say, putting the power law into general terms, that the chance of its not happening in
every
trial is:
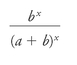
We want to find the number of trials where the chance that a double-six will not happen is even, or 1/2:
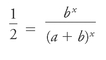
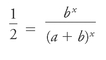
Using the splendid ability of algebra to re-jig equations in simpler forms, we multiply both sides by (
a
+
b
)
x
and by 2, then divide both sides by
b
x
, and get:
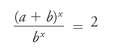
a
+
b
)
x
and by 2, then divide both sides by
b
x
, and get:
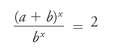
For many years, mathematicians would have been stumped at this point. But de Moivre had the benefit of logarithms, which allow us to manipulate equations to isolate exponents like
x
from the other elements:
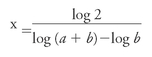
x
from the other elements:
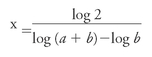
Logarithms ease calculation by considering any large number as a base raised to some power (as a million is also 10
6
). Instead of trying to multiply large numbers, we can simply add the powers of 10 that represent them, since 10
a
X 10
b
= 10
a+b
. So if
x
=10
a
, then
a
= log
x
. De Moivre was using “natural” logarithms, which have as their base not 10, but
e
, a mysteriously prevalent irrational number whose decimal expansion begins as 2.718281 . . . so 2 is a little less than
e
, roughly
e
0.7
.
6
). Instead of trying to multiply large numbers, we can simply add the powers of 10 that represent them, since 10
a
X 10
b
= 10
a+b
. So if
x
=10
a
, then
a
= log
x
. De Moivre was using “natural” logarithms, which have as their base not 10, but
e
, a mysteriously prevalent irrational number whose decimal expansion begins as 2.718281 . . . so 2 is a little less than
e
, roughly
e
0.7
.
Â
Once you've found the logarithm tables in the back of your old high-school textbook, you would have something good enough for most practical purposes. But de Moivre is not yet done. Instead of
a
and
b
, let's talk about 1 and
q
, so that we can say the odds against success are
q
to 1; that makes our basic equation (expressed in odds rather than probabilities):
a
and
b
, let's talk about 1 and
q
, so that we can say the odds against success are
q
to 1; that makes our basic equation (expressed in odds rather than probabilities):
De Moivre had a general method for dealing with crabbed, knotty expressions like log(1 + 1/q), which involved infinite series: that is, adding together an infinite number of terms, thus:
Er, yes . . . and exactly how is algebra helping us here? The formula
looks
clear enough, but then so do the instructions “Move this mountain using these tweezers.” De Moivre, however, noticed that, assuming
q
is big enough, all the terms after the first are so small as to make hardly any difference to the totalâparticularly since they alternately add and remove progressively tinier and tinier amounts. In fact, they are usually so small that we can dispense with them completely, allowing us to be reasonably correct without being exact. So, having done this major surgery, we are left with:
looks
clear enough, but then so do the instructions “Move this mountain using these tweezers.” De Moivre, however, noticed that, assuming
q
is big enough, all the terms after the first are so small as to make hardly any difference to the totalâparticularly since they alternately add and remove progressively tinier and tinier amounts. In fact, they are usually so small that we can dispense with them completely, allowing us to be reasonably correct without being exact. So, having done this major surgery, we are left with:
A quick glance above will remind you that log 2 is roughly 0.7. So, having started with a vague and general question, algebra offers us a startlingly specific result: given big enough odds against something, you can gauge how many trials are needed to have an even chance of seeing it happen by multiplying the odds by 0.7. This will apply to anything: roulette, cards, eclipses of the moon. In the case of de Méré's dice, the odds against rolling a double-six are 35 to 1 (as you know); 35 x 0.7 = 24.5 trials: exactly the answer Pascal got by calculating cases.
Infinite series and logarithms also gave de Moivre the key to understanding Pascal's Triangleâand, with it, the bell curve. A few pages ago we blithely said that if you wanted to know, say, the chance that
a
heads will appear in
n
tosses of a coin, you need only count
n
rows down the triangle and
a
across to find the coefficient. Easy enough for five or six trials, but imagine actually doing it for a series of 1,000 trials. Here are the tweezersâthere is the mountain. There are clearly good reasons for asking de Moivre and his algebra to help us.
a
heads will appear in
n
tosses of a coin, you need only count
n
rows down the triangle and
a
across to find the coefficient. Easy enough for five or six trials, but imagine actually doing it for a series of 1,000 trials. Here are the tweezersâthere is the mountain. There are clearly good reasons for asking de Moivre and his algebra to help us.
His attack on the problem took advantage of the two most important aspects of logarithms and infinite series: that logarithms allow you to get the result you need by adding logs rather than multiplying big numbers; and that infinite series can converge. That is (as we saw with the series for
1
+
1/q
), although the summing goes on forever, each new term makes progressively less and less difference to the total, so you can see where the series is heading even if you never quite get there. De Moivre then made one of those shifts of viewpoint that define genius in mathematics. Having teased out his formula for the middle term of the
n
th row of the triangle into an infinite series, he seemed to invite confusion and disaster by expanding each
term
in that series as an infinite series in itselfâwheels within wheels, new worlds riding on fleas' backs. Then, spreading out this vast quilt of terms, of sums of sums, he suggested that instead of adding
across
the rows, we should add
down
the columns, which reveal themselves as converging to neat and orderly formulae. For large numbers of trials, this infinite range of potential calculation collapses into two simple formulae for the approximate values (relative to the total, 2
n
) of the middle term and any other term
t
places away from the middle of row
n
of Pascal's triangle:
 You could, if you wish, use this formula to solve the problem of points; indeed, you would probably
You could, if you wish, use this formula to solve the problem of points; indeed, you would probably
have
to if you were playing more than, say, a hundred games.
1
+
1/q
), although the summing goes on forever, each new term makes progressively less and less difference to the total, so you can see where the series is heading even if you never quite get there. De Moivre then made one of those shifts of viewpoint that define genius in mathematics. Having teased out his formula for the middle term of the
n
th row of the triangle into an infinite series, he seemed to invite confusion and disaster by expanding each
term
in that series as an infinite series in itselfâwheels within wheels, new worlds riding on fleas' backs. Then, spreading out this vast quilt of terms, of sums of sums, he suggested that instead of adding
across
the rows, we should add
down
the columns, which reveal themselves as converging to neat and orderly formulae. For large numbers of trials, this infinite range of potential calculation collapses into two simple formulae for the approximate values (relative to the total, 2
n
) of the middle term and any other term
t
places away from the middle of row
n
of Pascal's triangle:
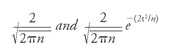
have
to if you were playing more than, say, a hundred games.
Other books
Woman with a Blue Pencil by Gordon McAlpine
The Scent of Murder by Felicity Young
Poisoned Petals by Lavene, Joyce, Jim
Exposed: New Adult Sport Romance (The Boys of Winter Book 5) by Violet Vaughn
Village of the Ghost Bears by Stan Jones
Peyton Riley by Bianca Mori
Bedtime Confessions (The Chambermaid's Tales - Short Stories) by Lynch, Sarah Michelle
Genesis by Karin Slaughter
Adrift 2: Sundown by K.R. Griffiths
The Sunflower: A Novel by Evans, Richard Paul