PopCo (11 page)

By the time the kit had been ‘adjusted’, all it contained was the Vigenère square. The Americans had made the most fuss over the original kit, saying that it contravened some law to do with preventing sophisticated encryption devices entering or leaving the country. (In fact, this is also why you can’t get full versions of some Internet browsers outside of the States, because it is illegal to export the encryption software that goes with them.) I thought it was amusing that my Vigenère square was still allowed through, however. Would a 9- to 12-year-old ever be able to actually use it to start a revolution or overthrow a government? Possibly. But the chapter on Vigenère is probably the one that all the kids actually skipped, because it really is far too complicated.
Vigenère ciphers, unlike mono-alphabetic ciphers, do usually require you to crack the key, although the ‘key’ for a Vigenère cipher is usually a simple word, rather than a whole, randomised alphabet. The cipher itself, however, is much more complicated and impossible to break down in the way you would approach a mono-alphabetic cipher.
Mono-alphabetic ciphers involve only one cipher alphabet. They are easy to crack because, once you know what ‘e’ and ‘t’ have been replaced with, the rest is just like completing an easy game of hangman. Poly-alphabetic ciphers, however, use several alphabets, at the same time. It’s hard to describe what a breakthrough it was when Alberti suggested as a possibility the use of several alphabets in one encipherment. Mono-alphabetic ciphers are
always
crack-able because of frequency analysis (even if the Sherlock Holmes method fails). But what if you could scramble the frequencies of letters by making different ciphertext letters stand for different plaintext letters throughout the message? This is what Alberti wondered. And he came up with a method that is, well, it’s genius really. You draw up a square made of twenty-six different versions of the alphabet, each one shifting by one letter each time (see table). Then you choose a short keyword, say RAIN. You write the keyword over and over again on the top of the plaintext to be enciphered like this:
| R | A | I | N | R | ||||||||||||||
| h | e | l | l | o | ||||||||||||||
| | ||||||||||||||||||
| R | A | I | N | R | A | I | N | R | A | I | N | R | A | I | N | R | A | I |
| t | h | e | h | a | r | d | e | s | t | o | f | t | h | e | m | a | l | l |
You then use the letter of the keyword to determine which ‘line’ of the Vigenère square you will use to encipher the letter below it. The ‘h’ in ‘hello’ enciphered using line R will be Y. ‘E’ enciphered using line A will be E (anything on line A will always be enciphered as itself, which is why many keywords don’t have an A in them). ‘L’ enciphered on line I will be T. The next ‘l’, however, will be enciphered on line N, making it Y. So the first word, ‘hello’, will now read: YETYF, which does not look like a mono-alphabetic version of ‘hello’ at all. There’s no clue to the ‘ll’ digraph any more, and ‘Y’ stands for two different letters.
The longer message from above is encrypted like this:
KHMURRLRJTWSKHMZRLT
You are never going to crack this with frequency analysis or guesswork. To crack this, you need to know that RAIN was used as the key. This is the only way into a Vigenère cipher. Sometimes keys can be arrived at by simple guesswork, of course. After the World Trade Centre attacks, one firm lost almost all its staff. The remaining few decided to try to keep the company going but were hindered by the fact that all the company passwords had been lost because everyone who knew them was now dead. The remaining employees then sat down and went through every aspect of their dead colleagues’ lives, noting down locations of holidays, pet names and so on until they actually cracked all the passwords. I was told this story by someone at work who’d been particularly touched by the company spirit shown by these people. I just thought it was one of the creepiest things I’d ever heard.
Vigenère square
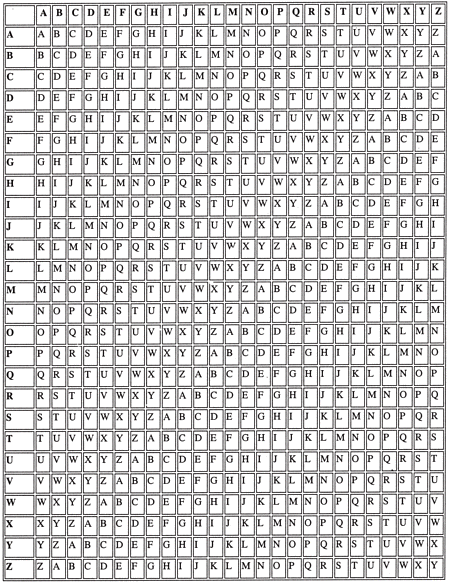
However, considering it is unlikely that you know the key word for a message someone does not want you to read, you have to proceed in a logical fashion and look for patterns in the message that will give you a clue to what the keyword might have been. Most messages would be vastly more complicated than any example. However, in our example, we can start to find patterns.
KHMURRLRJTWSKHMZRLT
The same trigraph, it seems, has been repeated in the message, implying one of two things. Either this is simply a random result of the encipherment, in which case it can’t help us, or perhaps it means that the same plaintext word has appeared under the same letters of the keyword and has been enciphered in the same way twice – in which case it will help us immeasurably.
It took a good 300 years after Alberti’s initial ideas for someone to work out how to crack Vigenère ciphers in this way. Charles Babbage, the crazy and brilliant inventor of the Difference Engine (the first computing machine), turned his attention to it after a bizarre argument with someone who thought he had invented poly-alphabetic ciphers for the first time.
‘
I have invented a new, unbreakable code!
’
‘
Well, actually, it’s not that new. It’s been around for
…’
‘
I tell you, my code is unbreakable!
’
‘
That’s as may be – but you did not invent it
.’
‘
Are you challenging me
?
’
‘
Well, yes, all right then, you imbecile
.’
‘
Let’s see you crack it, then!
’
So Babbage, who could not resist a challenge from someone so obviously brain-dead, even if the challenge was absurd, eventually
supplied us with our method. Babbage was a bit like this. As well as inventing the Difference Engine, he also invented the speedometer, the cowcatcher (a device fitted to trains to clear cattle from the tracks) and the basis of the modern postal system, where a letter can be sent anywhere in the country for the same price. He noted that if you could find patterns in a cipher like the one above, say the two instances of the trigraph KHM, you should then proceed the following way. Assuming you had a much longer piece of ciphertext, you would find as many instances as possible of repeated clusters of letters. Then you would count the letters from the beginning of each cluster to the beginning of the next. In our example above you would find twelve letters between the first K and the next one. What this tells you is that the keyword (the one that is written repeatedly above the plaintext during encipherment) must have a number of letters that is a factor of twelve i.e. 12, 6, 4, 3, 2 or 1, these being the numbers that divide into twelve. This makes sense, as we are assuming that the same letters repeat after twelve characters, in both the keyword and the plaintext message, resulting in the repeated cluster in the ciphertext. A two-letter key would have repeated six times before starting again; a twelve-letter key only once. With a longer piece of text it would be possible, usually, to narrow down the factors until the length of the word was obvious.
What happens next is rather complicated. If you had discovered that your keyword was four letters long, you would go through and label each letter in the ciphertext with a 1, 2, 3 or 4, depending on whether it would have been enciphered using the first, second, third or fourth letter of the keyword. Then you would perform frequency analysis on each set of letters; so for the letters marked with a 1, you would come up with a distinct frequency table which you could then compare with a list of normal frequencies. You would proceed the same way for each set of letters until you had each letter of the keyword, at which point you would decipher your message.
But this is not how I do it.
What I do is as follows. First of all I proceed the same way as Babbage would have done, trying to guess the length of the keyword by counting and factorising the letters between repeated clusters. But then I would be trying to find a short cut, being quite a fan of short cuts and not so much a fan of doing things the ‘right’ way,
or going the long way around in general. So what I always do next is look for every repeated trigraph in the text and then go through trying each one as ‘the’. I would be lucky with the sample above, as the first word is, of course, ‘the’. I would work the letters KHM back using the Vigenère square (if K equalled ‘t’, then the line of encipherment would have been R; if H equalled ‘h’, the line of encipherment would have been A and so on) and rather quickly come up with the following to work from: I would have a keyword that has a number of letters that is a factor of twelve and which possibly begins with the letters RAI. Intuition immediately tells me this could be the word RAIN. In fact, when I check in my dictionary I find other words that would fit as well: RAID, RAIL, and RAISIN, each being a word beginning with RAI and having a number of letters that is a factor of twelve. So what I do next is simply try them all. And of course, when I put the letters of the word RAIN repeating above the ciphertext, it unscrambles nicely.
I look down at my notebook, in which I have written the following:
XYCGKNCJYCJZSDSPPAGHDFTCRIVXU??????????? CJ and CJ??
Repetition too soon
.
The message is simply too short to have any useful patterns. Not that many short phrases actually contain convenient repetitions of the word ‘the’ or ‘and’ anyway. I yawn. Why has someone sent me this? Do they want me to read it or not? I sit there, listening to the noises outside in the dark, thinking how stupid this whole thing is. Why send a message with no key? I mean, it’s not as if I intercepted this – it was sent to me!
I am staring at the piece of paper so intently that it starts to blur beneath my eyes. The letters of the code merge and smudge together with the PopCo logo in the top left-hand corner and the
With
Compliments
lettering in the middle. And then I suddenly wonder: is the key in fact here, with the message? Vigenère used the concept of a ‘priming key’: could there be one here too?
With my heart playing fast percussion, and my brain suddenly alert, I write the ciphertext out on my pad again, cleanly, and write the letters POPCO repeating on top of it. My makeshift Vigenère square, which I have drawn on a piece of paper, gives me the following result:
| P | O | P | C | O | P | P | P | P | O | P | O | P | C | O | P | O | P | C | O | P | O | P | C | O | P | O | P | C |
| X | Y | C | G | K | N | C | J | Y | C | J | Z | S | D | S | P | P | A | G | H | D | F | T | C | R | I | V | X | U |
| i | k | n | e | w | y | o | u | w | o | u | l | d | b | e | a | b | l | e | t | o | r | e | a | d | t | h | i | s |
I knew you would be able to read this
. What kind of message is that? And who has sent it to me? I don’t like this very much, and the late-at-night factor doesn’t really help. I can’t relax now, so I pace the room smoking roll-ups until it is calm-ocean blue outside and only then do I get into bed.
Bertrand Russell once shared a dream with G. H. Hardy. Russell
dreamt he was on ‘the top floor of the University Library, about
A.D. 2100’, said Hardy. ‘A library assistant was going around the
shelves carrying an enormous bucket, taking down book after
book, glancing at them, restoring them to the shelves or dumping
them into the bucket. At last he came to the three large volumes
which Russell could recognise as the last surviving copy of
Principia Mathematica.
He took down one of the volumes
,
turned over a few pages, seemed puzzled for a moment by the
curious symbolism, closed the volume, balanced it in his hand
and hesitated
…’
From
The Man Who Loved Only Numbers
by Paul
Hoffman