Pythagorus (21 page)

‘Knowing' in a context like this was problematic for Plato, for it was not compatible with a universe in which the Forms could never be fully known. The Pythagoreans, however, had had an experience that Plato lacked. The discovery that mathematical logic and pattern underlie nature had apparently come as a shocking, intuitive impression for them. Mathematics and numbers were the rational, unconditional principles of the universe, waiting to be discovered, not deduced from things already known. Had they heard Plato speak about a search for ‘the invisible and incorporeal realm of Form', one of them might well have raised a hand and insisted they had found it. Their experience was that the vein of Truth (call it Forms, if you are Plato), mostly buried deep beyond the reach of the senses, at some rare points lies close enough to the surface to be perceived, like a vein of gold gleaming through a thin layer of dust and rock. The realm of music was one of those thin places.

Plato's pupils, and their pupils, continued to ponder the issues he had wrestled with, including the questions about whether the numbers are Forms. Speusippus allowed numbers and ‘mathematicals' to take the place of the Forms, while Xenocrates said that the Forms
were
the numbers. Both thought of themselves, and Plato, as Pythagoreans.

Many scientists and mathematicians today still hold to a Pythagorean faith that truth about the universe is inherently mathematical, and that it is possible to grasp at least bits of that truth by using our human level of mathematics. A few insist that mathematics is the only discipline in which some things are unarguably true and not subject to opinion, while others will not grant it that. Still others redefine ‘complete truth' as ‘truth that
human beings can discover
through mathematics', stretching the Pythagoreans beyond their own meaning and performing an end run around Plato.

The second Pythagorean
theme that inspired Plato was the creation and destiny of the soul. He applied the mathematical proportions that went into the creation of the ‘world soul' also to the human soul, and even described the soul in terms of a version of the Same and Different, reflecting two types of competing judgement – the ability and privilege of a human to say yes or no. For Plato, this free will was the essence of rational thought. But things were not easy for a soul living in a physical body on Earth, the Moon, or one of the planets. At the mercy of all the passions of its body, it inevitably got distorted and stirred up. Proper education could restore it to harmonious equilibrium by reawakening it to its link with the world soul. One way this could happen was through something heard and understood – the musical scale, the proportions of the world soul reproduced in sound.

The Pythagorean belief that a soul could ultimately escape the distorting influences of the world and be reunited with the divine level of the universe fascinated Plato. His ideas about immortality ranged from scepticism in his
Apology
to mystical speculation in his
Gorgias
, where Socrates attributes some of his thoughts about the soul to ‘some clever Sicilian or Italian' – an allusion to the Pythagoreans and probably to the philosopher Empedocles, who was often included under the Pythagorean banner. The dialogue ended with a myth in which souls witness the horrible punishment of incurable sinners in Hades. Plato, in this dialogue, did not argue for a doctrine of reincarnation, but his myth assumed that reincarnation occurred for those witnesses.

Plato probably wrote his
Meno
after his first visit with Archytas. In it, Socrates speaks of ‘wise priests and priestesses' whose authority is reliable, who teach about immortality and reincarnation – a bow to the Pythagoreans. Plato had Socrates attribute to those ‘priests and priestesses' the idea that because of what we have experienced earlier, much of what we know in this present life is ‘recollection'. This does not seem out of line with what Pythagoras claimed for himself, but Plato had something different in mind that he and his pupils thought was compatible with Pythagorean teaching.

As Plato interpreted the Pythagorean concept of the transmigrating soul, the possibility of escape from the parade of reincarnations lay in ‘becoming just and pious with wisdom', freeing the soul from fear and the passions and pains of the body. The highest goal was ‘becoming like god', as Plato phrased it in his
Theaetetus
. Several centuries later, the pagan neo-Platonist Porphyry (Pythagoras' biographer) listed Hercules, Pythagoras, and Jesus among those who had succeeded in this ultimate achievement of ‘becoming like god'.

‘Recollection', for Plato, did not however mean memories of past lives. Instead, it was the mysterious, innate, a priori knowledge that humans seem to possess, that cannot be explained by what one has learned in one's present life. Plato did not imply that anyone could recall acquiring this knowledge. As a demonstration, he used the geometric exercise that some believe reflected Pythagoras' proof of the Pythagorean theorem.

In this scene from Plato's
Meno
, Socrates and Meno are discussing a figure Socrates has drawn in the sand, a four-foot square. The task is to double the size of the square. Socrates intends to demonstrate that innate knowledge – not of the correct answer but of the underlying geometry that will lead to the correct answer – lies hidden in Meno's slave boy, waiting to be reawakened. Socrates is acting as a sort of midwife.

SOCRATES (to Meno):
Pay attention and I'll show you what he can discover by seeking the truth in my company, though I will only ask him questions, not teach him. Catch me if I seem to instruct him or explain instead of only asking him questions.
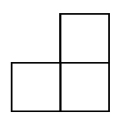
(Socrates erases previous figures in the sand and draws a four-foot square.)

Tell me, young man. Is this our square of four feet? Do you understand?

BOY:
It is.

SOCRATES:
Can we add another square, equal to it, like this?
(Draws.)

BOY:
Very well.

SOCRATES:
And here a third square, equal to each of the others?
(Draws.)

BOY:
Yes.

SOCRATES:
And now we can fill in this corner with another square? (
Draws.)

BOY:
Yes.

SOCRATES:
So now we have four equal squares?

BOY:
We do.

SOCRATES:
And how many times the size of our first square is this whole figure?

BOY:
Four times.

SOCRATES:
But we wanted one two times as large, remember?

BOY:
Yes.

SOCRATES:
Now, if we draw lines from corner to corner, like this, do they cut each of those squares in half? (
Draws.)

BOY:
They do.

SOCRATES:
And those four new lines create a new, central square?

BOY:
Yes.

SOCRATES:
Now think, how big is this new central square?

BOY:
I do not understand.

SOCRATES:
Again, here are our four squares. Does not each new line cut off half of one of them?

BOY:
Yes.

SOCRATES:
And how many of those halves are now included in this central square?

BOY:
Four of them.

SOCRATES:
How many are in each of the original squares?

BOY:
Two.

SOCRATES:
And the relationship of four to two is?

BOY:
Double.

SOCRATES:
So, how big is this figure?

BOY:
Eight feet.

SOCRATES:
On what base?

BOY:
This.
(He points to one of the diagonal lines.)

SOCRATES:
You mean the line going from corner to corner of the square of four feet?

BOY:
Yes.

SOCRATES:
Clever men call such a line a ‘diagonal'; so, using that name, is it your conclusion that the square on the diagonal of the original square is double its area?

BOY:
Most certainly, Socrates.

SOCRATES:
Well, Meno, do you think he has expressed any opinion that was not his own?

MENO:
No, they were all his own.