The Eternal Flame (42 page)

“You’ve asked for a very large amount,” Giusta said, glancing down at Carla’s application.

“We need to run the coherent light sources at a very high intensity, to make the energy valleys deep enough,” Carla explained. “But once we’ve mastered this—and once we can reproduce the effect in an ordinary solid—it will act as a net energy source. If we can get to that stage, the project won’t require any more sunstone at all.”

Giusta looked to Silvano, then the rest of her colleagues, but no one had any more questions for Carla. Even Councilors Massimo and Prospero—who’d been as merciless with Assunto on the hazards of dealing with the Object as they’d been with Carla at the previous hearing—seemed embarrassed by the alternative she was offering. The rebounder was already tainted by the inevitable comparisons with pre-scientific myths, but to claim that she could conjure her own Eternal Flame from a crystal of light sounded like the hyperbole of a stage magician: not even an appeal to genuine credulity so much as an invitation to share a joke.

“We’ll adjourn now,” Giusta said. “Thank you for your testimony.”

When the Councilors had left the chamber, Carla was alone with Assunto.

“If you change your mind, you’ll always be welcome on the orthogonal matter team,” he said.

“Thank you.” Carla had no ill feeling toward him; someone was always going to take over the project after she abandoned it, and she couldn’t blame Assunto for being a persuasive advocate for the cause. She’d benefited from his skills often enough, herself.

“I’ve had some thoughts about the Rule of One recently,” Assunto confided. “I’d be interested to hear what you think.”

“Of course.” Since the night with Patrizia and Romolo when they’d split the Rule of Two in half, Carla had had no success in explaining the simpler but equally mysterious principle that remained: once you took spin into account, you never found more than one luxagen in the same state.

“When we have a system of two luxagens,” Assunto began, “we need to think of it as a wave that depends on the positions of both particles. So if one particle is mostly
here
and another is mostly
there
, we need the wave to have a bump where the combination of positions spells that out.”

He sketched what he meant.

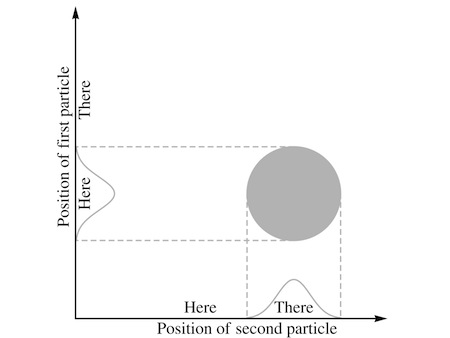
“Right,” Carla said. “That’s how I think of it too.”

“But there’s a problem,” Assunto claimed. “Suppose we compare that with another wave, where we swap the two particles.”

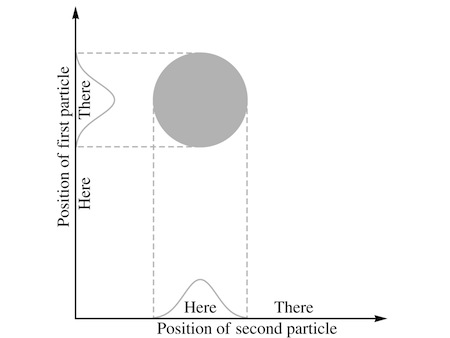
“That’s really the same thing,” Carla protested. “A luxagen is a luxagen; it makes no sense to say that it’s the ‘first luxagen’ in one location and the ‘second one’ in the other. Unless they have different spins, and you’re using that to tell them apart?”

Assunto said, “No, no. Forget about spins for the moment, or just assume the spins are identical. Take it as given that we really can’t tell these luxagens apart.”

“Then the two situations are exactly the same,” Carla replied.

“So you’re saying there are two different waves that can be used to describe the same physical situation?”

“Yes,” Carla insisted. “It’s just a convention, a naming scheme: you have to make a choice, but the choice itself makes no difference.”

“All right,” Assunto agreed, though his assent sounded distinctly provisional. “But now suppose I want to
compare
the wave for this pair of luxagens with the wave for another pair that are in roughly the same positions. How exactly should I make the comparison? Which of the two waves should I use in each case? There are four possibilities in all. Half those possibilities give the two pairs of luxagens very similar waves… while the other half give them very different waves!”

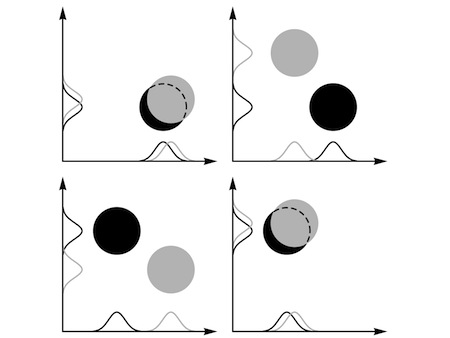
Carla thought for a while. “Surely you just need to use the same scheme for both? I mean, it’s obvious that there ought to be some overlap between the two waves—and if you use different schemes there’s no overlap at all.”

“But if you can’t tell the luxagens apart,” Assunto pressed her, “how do you define ‘the same scheme’? How do you actually
pick
which luxagen of the pair gets its position assigned to which axis?”

“Hmm.” He’d forced her into a contradiction; she’d claimed the choice of schemes didn’t matter, but now she’d starting talking about the importance of selecting the right one, case by case.

“Do you have to peek at their locations first, then make sure you give the same axis to whichever particles are closest together?” Assunto was gently mocking her now.

“Hardly.” Carla stared at the four diagrams. She was starving, and she’d barely slept for the last three nights, but she wasn’t going to let him make a fool of her with this problem.

“You use both schemes,” she said finally. “Simultaneously. You
add
the wave where you use the first axis for the first particle to the wave where you use it for the second particle.”

She sketched the idea.

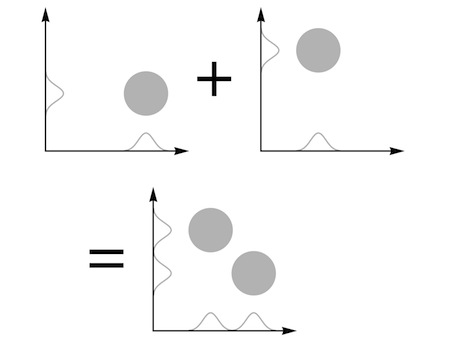
“The wave for the whole system is completely symmetrical,” she said. “It makes no difference if you swap the axes, or swap the particles. And when you compare two situations with two particles in roughly the same two places, you’re guaranteed to get a sensible result with some overlap between the waves.”

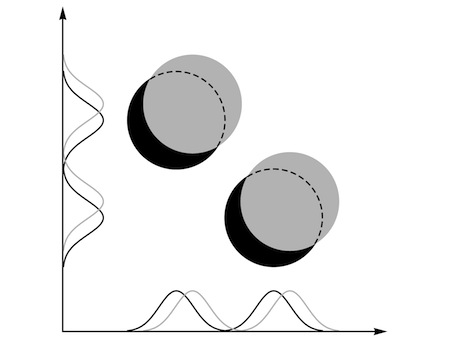
“I think you’re right,” Assunto said. He sounded pleased that they’d reached the same conclusion—but he wasn’t yet finished with the subject. “That’s one way of doing wave mechanics with identical particles.”

“
One
way?”

“It looks like the most natural choice,” he said. “But I don’t believe it’s the only one. What about this?”

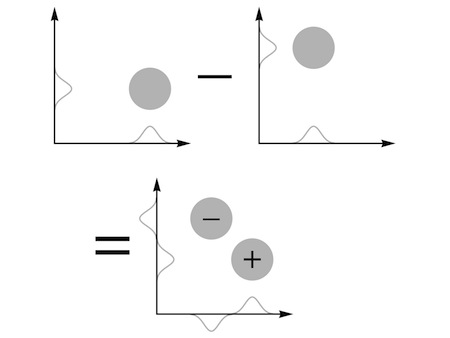
“You subtract the waves instead of adding them?” Carla was confused. “But subtract them in what order? Aren’t you asking for the same problem again: which of two identical particles do you call the first?”

“No, because it
makes no difference
,” Assunto replied. “If you change the order, you just turn the whole wave upside down—and an overall change of sign like that has no effect on the physics of the wave.”

That was true. “But what’s the point?” Carla asked. “You end up with a wave with two bumps of opposite sign, instead of two identical bumps. The mathematics becomes a bit more complicated, but the final answers all turn out the same.”

“The final answers don’t depend on putting the particles in any particular order,” Assunto said. “But what makes you think they’re the same when you subtract the schemes as when you add them?”

Carla examined the diagram again. “If the particles get close together, the two waves you’re subtracting start to overlap.”

“Yes.”

“And if they’re in
exactly the same state
,” she realized, “you get nothing, zero.”

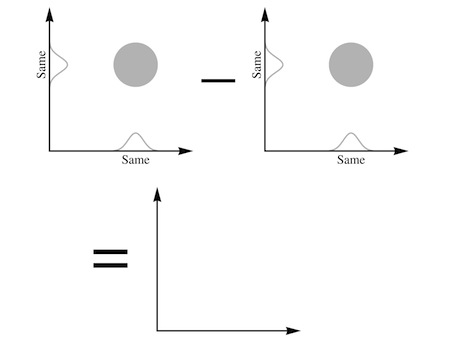
“Precisely.” Assunto buzzed softly. “Does that remind you of anything?”

“The Rule of One,” Carla said. “So you’re saying that you can never have two luxagens in the same state, because they follow this subtraction scheme, where the total wave for the pair would vanish?”

“Yes!”

“But why? Why can’t they follow the addition scheme?”

“It must be linked to the luxagen’s spin somehow,” Assunto said. “Think about the similarities! Take a luxagen, with spin of a half, and rotate it by a full turn: the rotation gives you the
opposite
of the original luxagen wave. A transformation that leaves most things unchanged leads to a change of sign. And now it turns out that we can get the Rule of One if we assume that
swapping two luxagens in a pair
—another transformation that might be expected to have no effect at all—also changes the sign of the overall wave.”