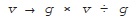The Eternal Flame (54 page)

The length of a vector can be found from the four-dimensional version of Pythagoras’s Theorem. We write the length of the vector
v
as |
v
|, and it is related to the size of its components in each direction by:

When two vectors are multiplied together, the length of the resulting vector is just the product of the lengths of the original vectors:

Given a vector
v
it’s often useful to talk about its
conjugate
, which we write as
v
* and define as the vector whose components in the three space directions are the opposite of those of
v
, while its component in the time direction is exactly the same as that of
v
:

Multiplying a vector by its own conjugate gives a very simple result:

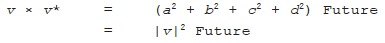
Since the direction Future acts like the number one in this system, if
v
has a length of one its conjugate
v
* will also be its inverse,
v
^-1
. If the length of
v
is not one, we can still find its inverse from its conjugate by dividing by the square of its length:

Because of this close relationship between the
conjugate
of a vector and its
inverse
, it’s not hard to see that if we take the conjugate of a product of vectors we need to reverse their order, just as we do with the inverse:

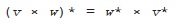
The Future component of the product of one vector with the conjugate of another,
v
×
w
*, carries some useful geometric information about the two vectors:

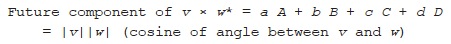
The quantity on the right hand side of the first equation, where we multiply the four components (
a
,
b
,
c
,
d
) of
v
and (
A
,
B
,
C
,
D
) of
w
and add up the results, is known as the
dot product
of the two vectors. As the second equation shows, it depends only on their lengths and the angle between them.

Any rotation of four-dimensional space can be achieved by fixing two vectors whose length is one, say
g
and
h
, and then multiplying on the left with
g
and dividing on the right with
h
. So the vector
v
is rotated by:

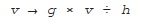
For example, a rotation that swaps North and South and also Future and Past, while leaving all directions orthogonal to these unchanged, can be achieved by setting
g
= South and
h
= North.

How can we be sure that this operation really is a rotation? For a start, it’s easy to see that the length of
v
is unchanged, since |
g
|=|
h
|=|
h
^-1
|=1 and:

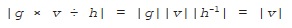
We can also look at what happens to the angle between two vectors when we perform the same operation on both of them, by looking at the effect on
v
×
w
*:

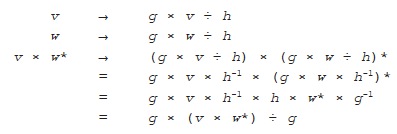
The Future component of
v
×
w
* is left unchanged by this operation, since
g
× Future ÷
g
= Future. And since the Future component of
v
×
w
* determines the angle between
v
and
w
—along with their lengths, which we know are unchanged—that angle is also unchanged.

All rotations that involve only the three dimensions of space can be achieved by restricting the original formula to the case where
h
=
g
: