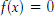The John Green Collection (64 page)

which means that when I give you the number
x
, the function instructs you to take
x
and multiply it by itself (i.e., to compute
x
²
) and return that new number to me. Using the function, we can plot
all
points of the form (
x,f(x)
). Those points together will form some kind of curve in the plane, and we call that curve the “graph of the function.” Consider the function
f(x) = x
²
. We can plot the points (1,1), (2,4), and (3,9).

In this case, it might help to plot the additional points (0,0), (–1,1), (–2,4), and (–3,9). (Remember that if you take a negative number and multiply it by itself, you get a positive number.)

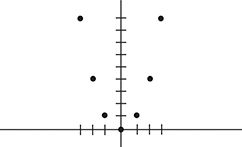
Now, you can probably guess that the graph will be a curve that looks something like this:

Unfortunately, you’ll notice that this graph doesn’t do a particularly good job of representing relationships. The graphs that Colin wants to use for his
Theorem all need to cross the
x
-axis twice (once for when a couple starts dating, and once for the dumping), whereas the graph we drew only touched it once. But this can easily be fixed by using slightly more complicated functions. Consider, for example, the function
f(x) = 1-x
²
.

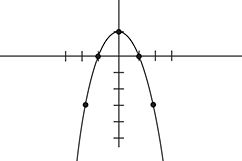
This graph is quite familiar to Colin—it’s a graph of a short relationship in which he’s dumped by the girl (we know that the girl dumps Colin because the graph is above the
x
-axis between the first kiss and the dumping). It’s the graph that tells an outline of the story of Colin’s life. Now all we need to do is figure out how to modify it so as to flesh out some details.

One of the great themes of twentieth-century mathematics has been the drive to study everything in “families.” (When mathematicians use the word “family,” they mean “any collection of like or related objects.” E.g., a chair and a desk are both members of the “furniture family.”)

Here’s the idea: a line is nothing more than a collection (a “family”) of points; a plane is simply a family of lines, and so forth. This is supposed to convince you that if one object (like a point) is interesting, then it will be even more interesting to study a whole family of similar objects (like a line). This point of view has come to completely dominate mathematical research over the last sixty years.

This brings us to the third piece of Colin’s Eureka puzzle. Every Katherine is different, so each dumping that Colin receives at the hands
of a new Katherine is different from all the previous ones. This means that no matter how carefully Colin crafts a
single
function, a
single
graph, he’ll only ever be learning about a
single
Katherine. What Colin really needs is to study all possible Katherines and their functions, all at once. What he needs, in other words, is to study the
family
of all Katherine functions.

And this, at last, was Colin’s complete insight: that relationships can be graphed, that graphs come from functions, and that it might be possible to study all such functions at once, with a single (very complicated) formula, in such a way that would enable him to predict when (and, more importantly, whether), any prospective Katherine would dump him.
⁸⁵

Let’s give an example of what this might mean; in fact, we’ll talk about the first example that Colin tried. The formula looks like this:

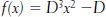
In explaining this expression, I certainly have a lot of questions to answer: first off, what on earth is
D
? It’s the Dumper/Dumpee differential: you can give anybody a score between 0 and 5 depending on where they fall on the spectrum of heartbreak. Now, if you’re trying to predict how a relationship between a boy and girl will work out, you begin by taking the boy’s D/D differential score and subtracting from it the girl’s D/D differential score and calling the answer
A.
(So if the boy is a 2 and the girl is a 4, you get D = −2.)

Now, let’s see what effect this has on the graph. In the example I just gave where the boy gets a 2 and the girl gets a 4, so that
D
= −2, we have

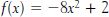
whose graph looks like this:

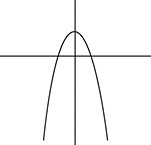
As you can see, the relationship doesn’t last too long, and the girl ends up dumping the boy (a situation Colin is quite familiar with).

If, instead, the boy was a 5 and the girl was a 1, we’d have D = 4, so that

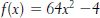
which has the following graph:

This relationship is even shorter, but it seems even more intense (the peak is remarkably steep), and this time the boy dumps the girl.

Unfortunately, this formula has problems. For one thing, if D = 0, that is, if they’re equal Dumpers or Dumpees, then we get