The Lives of Others (42 page)

He stopped for a bit, looked at his teacher for an instant, immediately looked down again, then once again faced the board. He wrote:

From the above, sin
²
x
+
cos
²
x = 1.

Again he glanced briefly at Mr Adhikari. This time he gathered up enough courage to ask, ‘Shall I prove it?’

Swapan Adhikari shook his head and said, ‘No. Go back to your seat now.’ He was going to add, redundantly, he felt, ‘Pay heed to what I’m teaching next time’, but decided not to.

The boy meekly returned to his bench, his expression of desired erasure unchanged; not an atom of triumphalism or self-satisfaction anywhere. But that was not what was going through Swapan Adhikari’s mind at all. What dazed him was the clarity of the boy’s mind, of his impeccable return to first principles and proceeding from there. This new pupil in Class Seven had just elucidated a topic that he was three years away from being taught in school.

At home he looked at the bundle of papers he had confiscated: a collection of different kinds, ruled, plain, of different sizes, quality and colour, all held together by a rusty safety pin. The first ten or twenty seconds of browsing was a blur of numbers and alphabets and faux-equations, and then it hit him with a force that could have lifted him clean off the ground if it had had a material correlate – the boy was trying to prove Fermat’s two-square theorem. First, over several sheets there was an ultimately successful attempt to prove that the set of all sums of two squares was closed under multiplication. Using that as a starting point, he had embarked on a proof of p = x
²
+ y
²
iff p ≡ 1 (mod 4). There were shortcuts the boy clearly did not know about, so he had spent a lot of time reinventing the wheel. Shorn of the circularities, the reiterated steps, the occasional cul-de-sacs, he had been engaged in working out from scratch Euler’s proof by infinite descent. The notations were unconventional, there was a lot of chasing of his own tail, but there it was: a messy proof, not parsimonious, not austere, but a proof nevertheless, one even assuming a knowledge of relatively prime and – miraculous, this – a feeling for the notion of finite difference.

On another page there were series of numbers, written one after the other, line after line. A few minutes’ contemplation of those revealed that the boy was trying to feel his way towards prime gaps and twin primes. On yet another, an innocently formulated: ‘if a > 1, then a . . . P . . . 2a?’; the boy did not know that he had stumbled upon Bertrand’s theorem. Swapan Adhikari had to prove it in his final exams for the BA (Hons) degree. There was a long-winded working-out of the binomial theorem – he must have had access to some kind of intermediate mathematics books to symbolise binomial coefficients correctly as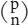
and even a knowledge of combinatorials in his use of n! – and its correct proof using induction. Buried deep within was some incipient thinking about asymptotic equality leading on from logarithms and the prime counting function.

Swapan Adhikari had never felt such a sustained sense of disbelief. Question after question rose and fell in him like the peals of giant bells – Was this all intuitive? How could it
be
? Was someone, a relative, a maths professor, guiding him? If so, why the idiosyncratic language? The symbols were all wrong, the competence in mathematical notation and the sequentiality of steps amateurish, as if a child were trying to build the engine of his car with the pieces of his Meccano set. Where did he live? Where was he before he came to St Lawrence? Could it have been a preternaturally gifted teacher at that school? What else had he been feeling his way towards? How could someone like this, with such an innate understanding and feel for the music of abstraction, be untrained? Yet untrained he seemed to be. Where had he got hold of books on algebra? This boy was thirteen years old . . . the fact was like repeated socks to his jaw. This was not possible. There was something under his nose that he was failing to notice, that would clear up the mystery, and he would be left feeling a bit foolish at his incomprehension.

But with every nugget of meaning that Swapan Adhikari scooped out from the mess, one thing only stood out with the incontrovertibility of a basic axiom – he almost did not dare think it – this boy was a . . . genius. The slightest touch of hysteria brushed against him. Then it seemed to intensify – he flipped again through the pages and found his eyes welling up. Something from the magic world of childhood reading reappeared: the story of Byangoma and Byangomi, the bird-couple who knew the fates of the princes and men who fell asleep under the tree in which they lived, the birds who talked about the future of those mortals, alerting them to what was to come. It seemed to him that those magical creatures had guided the boy through these matters that should have been beyond him.

He could not tell why he found it so deeply affecting that Swarnendu had tried to go back to first principles, at almost every step of the way, in order to prove the theorem. It was so pure, so innocent. It was like watching a child, except this child was touched by a kind of divine fire, a child in whose presence you felt like bowing your head.

The room was densely blue with smoke: he had made his way through two packets of Charminar.

That was when he decided to drop in on his old, now nearly demented, professor, Ashish Roy, the man who had come close to solving some of the open problems in number theory, including the n
²
+ 1 conjecture, only to have a series of nervous breakdowns take it all away from him. The rumour within mathematician circles in Calcutta was that he had had a glimpse into the mind of god, into god’s book of numbers, and had been driven insane as a result.

Then came the second attack of incredulity. Ashish Roy not only knew Swarnendu – Sona, he called him – but they were near-neighbours. At the time Swapan Adhikari had briefly wondered about the statistical probability of the joining of three random dots – Ashish Roy, Swarnendu Ghosh and himself – distributed amidst a dense scatter, seven million to be exact, but non-mathematicians never believed you if you said there were more coincidences in life than in books, concurrences at which they did not bring illogical charges of ‘Oh, that’s unbelievable!’ that they reserved for the fictional variety. Why would there be saws such as ‘The world is such a small place’ and ‘What goes around must come around’ if coincidence did not form a regularly occurring part of life?

Ashish-da had leafed through Swarnendu’s workbook. The silence in the room had been punctuated by the wonderfully aleatory music of a brief giggle; an ‘eeeesh-tsk-tsk-tsk’ of regret, the kind that resulted from watching your favourite candidate in a race falling slightly behind; a long rumble of laughter; a deep ‘ooooh’; several ‘a-ha-ha’s of admiration – all widely spaced from each other. Behind the random soundtrack had been his ever-present anxiety that Ashish-da’s wife, who blamed mathematics for the dark pit into which their lives had fallen, could have entered the room at any minute and broken up their mostly silent meeting. She kept her husband under continual surveillance, forbidding any of his mathematician friends, ex-colleagues or students from visiting.

‘Have you seen, have you seen, a list of arithmetic progressions, he’s on the brink of Dirichlet’s theorem.’

Long silence.

‘I saw the proof first in ’37, Harding-saheb drew my attention to it. Oh, Harding-saheb, what a nice man he was. A giant moustache. You could hardly make out the words behind it. He missed out key steps in a proof, assuming that you’d know it, or that it was too obvious to be spelled out.’

Another pause, this time dotted with odd snuffling and guttural noises.

‘Jaaaah, it slipped my hands, it slipped.’

A huge sigh followed by another protracted lull.

‘I thought you and that other young man, the one who left, what was his name, I thought you would go too, but . . . yes, you two could see if the first and second Hardy-Littlewood conjectures could . . . could . . . nah, the bell rang.’

Then the closest Ashish Roy came to the nub, a one-point touch like that of a tangent to a curve, then off and away again: ‘Maybe we could all pass the baton on to this boy. Invest him with all our hopes. But we need to help him. Ufff, if he arrives at Dirichlet by pure intuition’ – here he rubbed his hands the way a miser would, contemplating his hoard of gold – ‘you could talk to the student who’s abroad, what’s his name? I can’t remember anything nowadays, my brain is a sieve, sieve ha-ha-ha-ha-ha, a sieve for primes like that Greek had, a sieve ha-ha-ha-ha-ha, that was a good one, no? What do you say, eh? But some books may tide him over the short term . . . Hardy & Wright, maybe . . .’

Swapan Adhikari had got what he had wanted. Something had been clarified for him.

Finally, after weeks of mental preparation, Swapan Adhikari sits down to write to his friend Ayan Basu, now an associate professor of mathematics – ‘the one who left’, the one he was supposed to join, until fate dealt him a crippling card . . .

Dear Ayan
, he begins:

I hope this finds you in good health and spirits. I have no excuse for the large gap that has fallen between this and your last letter to me except to cite the usual mess that is life. But I’m writing to you with a request you may well find a bit unusual. A little bit of the back-story, first. You may find it unbelievable too, as I did, but please be patient. There is a boy in my school, a Swarnendu Ghosh, thirteen going on fourteen, in Class Seven.

He stops there. How can he take it forward, short of sending Ayan the boy’s exercise book for him to experience it first hand? What else can he add about Swarnendu? The gentle questioning of the boy in the staffroom and outside the school yielded up very little. He had the strange capacity of returning pure silence to direct questions in a way that made the interrogator feel intrusive and, ultimately, embarrassed. It was Swapan Adhikari who had felt flustered and discomfited, as if the ordinary power dynamics between teacher and pupil had been reversed. About the mathematics, the boy had not been able to say anything at all except to confirm that it was his own work, done unaided in his private leisure time.

‘I . . . I think . . . and then . . . then the numbers take me from . . . from one step to another,’ he had said haltingly, struggling to put words to experience.

Other information too was minimal; he had refused to talk about his parents or any other members of his family, but had told Swapan Adhikari which school he had attended before he came to St Lawrence. Now, writing about him to Ayan, he realises that the boy is an absence, a geometric gap bounded by the facets of the different elements of analytic number theory that he had tried to think about.

A tiny spark at lunch. The family has long stopped sitting down together to eat, a result of the absence of Sandhya’s kind, superintending eye. Purnima and Charubala, not on talking terms for a good while now, go through the motions of sitting at the same table around half-past one or two every afternoon, even though they do not speak to each other directly. If this non-communication was a cause of active tension when the hostilities began, now it has calcified into something inorganic, like a darkening water mark down an external wall, that can be ignored; it seems the natural course of things. The age-old oppugnant relationship between mother and daughter-in-law in this instance is an apparently paradoxical variant: Purnima feels she has failed to elevate her husband to the top position in Charubala’s regard. After years of jockeying, the accreted failure, by now densely settled into a stratum of fury and resentment, could not be checked and has started bubbling up under the increasingly flimsy superstructure of family unity and its foot soldiers – respect, obedience, love.

How like that Geography chapter on volcanoes, thinks Arunima, as she picks out tiny bones from her piece of fish, a time-tested strategy for deferring the act of eating until so late that her plate is eventually cleared away, saving her yet again from eating the rubbish that gets served day after day, unchangingly, for lunch: rice, dal, a mushy medley of vegetables, a watery fish stew, the fish chosen deliberately, she felt, for maximum boniness; it is an invitation to starve yourself, that fish.