Read Why Beauty is Truth Online
Authors: Ian Stewart
Why Beauty is Truth (59 page)
The octonions have eight units: the ordinary number 1, and seven others called e
1
, e
2
, e
3
, e
4
, e
5
, e
6
, and e
7
. The square of any of these is â1. The diagram determines the multiplication rule for the units. Suppose you want to multiply e
3
by e
7
. Look in the diagram for points 3 and 7 and find the line that joins them. On it, there is a third point, which in this case is 1. Following the arrows, you go from 3 to 7 to 1, so e
3
e
7
= e
1
. If the ordering is back to front, throw in a minus sign: e
7
e
3
= âe
1
. Do this for all possible pairs of units, and you know how to do arithmetic with octonions. (Addition and subtraction are always easy, and division is determined by multiplication.)
Graves and Cayley didn't know about this connection with finite geometry, so they had to write out a multiplication table for octonions. The Fano plane pattern was discovered later.
For many years, the octonions were merely a minor curiosity. Unlike quaternions, they had no geometrical interpretation and no application in science. Even within pure mathematics, nothing seemed to follow from them; no wonder they fell into obscurity. But all this would change with the realization that the octonions are the source of the most bizarre algebraic structures known to mathematics. They explain where Killing's five exceptional Lie groupsâG
2
, F
4
, E
6
, E
7
, and E
8
âreally come from. And the group E
8
, the largest of the exceptional Lie groups, shows up
twice
in the symmetry group that forms the basis of 10-dimensional string theory, which has unusually pleasant properties and is thought by many physicists to be the best candidate yet for a Theory of Everything.
If we agree with Dirac that the universe is rooted in mathematics, then we could say that a plausible Theory of Everything exists because E
8
exists, and E
8
exists because the octonions exist. Which opens up an intriguing philosophical possibility: the underlying structure of our universe, which we know to be very special, is singled out by its relationship to a unique mathematical object: the octonions.
Beauty is truth, truth beauty. The Pythagoreans and Platonists would have loved this evidence of the pivotal role of mathematical patterns in the structure of our world. The octonions have a haunting, surreal mathematical beauty, which Dirac would have seized upon as a reason why 10-dimensional string theory has to be true. Or, if unhappily proved false, is nevertheless more interesting than whatever
is
true. But we have learned that beautiful theories need not be true, and until the verdict on super-strings is in, this possibility must remain pure conjecture.
Whatever its importance in physics, the circle of ideas surrounding the octonions is pure gold for mathematics.
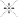
The connection between the octonions and the exceptional Lie groups is just one of many strange relationships between various generalizations of the quaternions and the frontiers of today's physics. I want to explore some of these connections in enough depth for you to appreciate how remarkable they are. And I'm going to start with some of the oldest exceptional structures in mathematics, formulas about sums of squares.
One such formula derives naturally from the complex numbers. Every complex number has a “norm,” the square of its distance from the origin. The Pythagorean theorem implies that the norm of
x
+
iy
is
x
2
+
y
2
. The rules for multiplying complex numbers, as laid down by Wessel, Argand, Gauss, and Hamilton, tell us that the norm has a very pretty property. If you multiply two complex numbers together, then the norms multiply too. In symbols, (
x
2
+
y
2
)(
u
2
+
v
2
) = (
xv
+
yu
)
2
+ (
xu
â
yv
)
2
. A sum of two squares times a sum of two squares is always a sum of two squares. This fact was known to the Indian mathematician Brahmagupta around 650, and to Fibonacci in 1200.
The early number theorists were fascinated by sums of two squares, because they distinguished two different types of prime number. It is easy to prove that if an odd number is the sum of two squares, then it must be of the form 4
k
+ 1 for some integer
k.
The remaining odd numbers, which are of the form 4
k
+ 3, cannot be represented as the sum of two squares. However, it is
not
true that every number of the form 4
k
+ 1 is a sum of two squares, even if we allow one of the squares to be zero. The first exception is the number 21.
Fermat made a very beautiful discovery: these exceptions can never be prime. He proved that on the contrary, every
prime
number of the form 4
k
+ 1 is a sum of two squares. By applying the above formula for multiplying sums of two squares together, it then follows that an odd number is a sum of two squares if and only if every prime factor of the form 4
k
+ 3 occurs to an even power. For instance, 45 = 3
2
+ 6
2
is a sum of two squares. Its prime factorization is 3 Ã 3 Ã 5, and the prime factor 3, which has the form 4
k
+ 3 with
k
= 0, occurs to the power twoâan even number. The other factor, 5, occurs to an odd power, but that's a prime of the form 4
k
+ 1 (with
k
= 1), so it doesn't cause any trouble.
On the other hand, the exception 21 is equal to 3 Ã 7, which are both primes of the form 4
k
+ 3, and here each occurs to the power 1, which is oddâso that's why 21 doesn't work. Infinitely many other numbers don't work for the same reason.
Later, Lagrange used similar methods to prove that
every
positive whole number is a sum of four squares (zero permitted). His proof used a clever formula discovered by Euler in 1750. It is similar to the one above, but for sums of four squares. A sum of four squares times a sum of four squares is itself a sum of four squares. There can be no such formula for sums of three squares, because there exist pairs of numbers that
are both sums of three squares but whose product is not. However, in 1818 Degen found a product formula for sums of
eight
squares. It is the same formula that Graves discovered using octonions. Poor Gravesâhis discovery of octonions, which was original, was credited to someone else; his other discovery, the eight-squares formula, turned out not to be original.
There is also a trivial product formula for sums of one squareâthat is, squares. It is
x
2
y
2
= (
xy
)
2
. This formula does for real numbers what the two-squares formula does for complex numbers: it proves that the norm is “multiplicative”âthe norm of a product is the product of the norms. Again, the norm is the square of the distance from the origin. The negative of any number has the same norm as its positive.
What of the four-squares formula? It does the same thing for quaternions. The four-dimensional analogue of the Pythagorean theorem (yes, there is such a thing) tells us that a general quaternion
x
+
iy
+
jz
+
kw
has norm
x
2
+
y
2
+
z
2
+
w
2
, a sum of four squares. The quaternionic norm is also multiplicative, and this explains Lagrange's four-squares formula.
You will probably be ahead of me by now. Degen's eight-squares formula has a similar interpretation for octonions. The octonion norm is multiplicative.
Something very curious is going on here. We have four types of evermore-elaborate number system: the reals, complexes, quaternions, and octonions. These have dimensions 1, 2, 4, and 8. We have formulas that say that a sum of squares times a sum of squares is a sum of squares: these apply to 1, 2, 4, or 8 squares. The formulas are closely related to the number systems. More intriguing still is the pattern of the numbers.
1, 2, 4, 8âwhat comes next?
If the pattern continued, we would confidently expect to find an interesting 16-dimensional number system. Indeed, such a system can be constructed in a natural way, called the CayleyâDickson process. If you apply that process to the reals, you get the complexes. Apply it to the complexes, you get the quaternions. Apply it to the quaternions, you get the octonions. And if you plow ahead and apply it to the octonions, you get the
sedenions
, a 16-dimensional number system, followed by algebras of dimension 32, 64, and so on, doubling at every step.
So there is a 16-squares formula, then?
No. The sedenion norm is not multiplicative. Product formulas for sums of squares exist
only
when the number of squares involved is 1, 2, 4, or 8. The law of small numbers strikes again: the apparent pattern of powers of two grinds to a halt.
Why? Basically, the CayleyâDickson process slowly destroys laws of algebra. Every time you apply it, the resulting system is not quite as well behaved as the previous one. Step by step, law by law, the elegant real number system descends into anarchy. Let me explain in more detail.
The four number systems have other features in common aside from their norms. Their most striking feature, which qualifies them as generalizations of the real numbers, is that they are “division algebras.” There are many algebraic systems in which notions of addition, subtraction, and multiplication are valid. But in these four systems, you can also divide. The existence of a multiplicative norm makes them “normed division algebras.” For a while, Graves thought his method of going from 4 to 8 could be repeated, leading to normed division algebras with 16, 32, 64 dimensions, any power of two. But he hit a snag with the sedenions and began to doubt whether a 16-dimensional normed division algebra could exist. He was right: we now know that there exist only four normed division algebras, of dimensions 1, 2, 4, and 8. And there is no 16-squares formula like Graves's eight-squares formula or Euler's four-squares formula.
Why is this? At every step along the chain of powers of two, the new number systems lose a certain amount of structure. The complex numbers are not ordered along a line. The quaternions fail to obey the algebraic rule
ab
=
ba
, the “commutative law.” The octonions fail to obey the associative law (
ab
)
c
=
a
(
bc
), though they do obey the “alternative law” (
ab
)
a
=
a
(
ba
). The sedenions fail to form a division algebra and have no multiplicative norm either.
This is far more fundamental than just a failure of the CayleyâDickson process. In 1898, Hurwitz proved that the only normed division algebras are our four old friends. In 1930, Max Zorn proved that these same four algebras are the only alternative division algebras. They truly are exceptional.
This is the sort of thing pure mathematicians, with their Platonist instincts, love. But the only really important cases for the rest of humanity seemed to be the real and complex numbers, which were of massive practical importance. The quaternions did show up in some useful if esoteric applications, but the octonions shunned the limelight of applied science.
They seemed to be a pure-mathematical dead end, the sort of pretentious intellectual nonsense you would expect from people with their heads in the clouds.
