X and the City: Modeling Aspects of Urban Life (26 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

Question:
jerk
is defined as the time derivative of the acceleration, that is,
j
(
t
) =
da
/
dt
. Do you think there is any usefulness to defining a quantity similar acceleration noise (as in equation (8.10), namely
jerk noise
?

Figure 8.7. Headway geometry for a two-lane highway.
=
T
h
: OVERTAKING IN THE CITY
We conclude this chapter with a simple mathematical model of overtaking and passing on a straight section of road. In
Figure 8.7
a vehicle in the right lane moves into the left lane at speed
V
1
>
V
0
to overtake and pass a slower-moving vehicle. The equations, if not the diagram, are independent of which side of the Atlantic the vehicle resides! The
headway T
H
is the time gap between adjacent oncoming vehicles moving at speed
V
2
.
Clearly,

Suppose that a reasonable time in which to complete a passing maneuver by a car traveling at 55 mph is 8 seconds, the headway required for an oncoming vehicle traveling at 65 mph in the opposing lane is
T
H
≈ 15 seconds. For interstates or other multilane highways, the needed gaps are smaller; we just change the sign of
V
2
(obviously we require
V
1
<
V
2
). In this case for the same speeds
T
H
≈ 1.2 seconds!
PROBABILITY IN THE CITY

There are many topics under the umbrella “road traffic” that are amenable to mathematical investigation. Examples include traffic flow on the open road and at intersections, parking problems, accident rates, design of road systems for new towns and expanding cities, traffic lights and other control systems, transportation and scheduling problems, to name but a few. And as in so many aspects of mathematical modeling, there are two basic choices: to define the problem in a
deterministic
or a
probabilistic
context. The former can subdivide farther into continuum or discrete (or equivalently, macroscopic or microscopic) approaches, each with its own advantages and disadvantages. In the continuum approach the flow of traffic is treated as a fluid; properties of individual vehicles (“fluid particles”) are not considered. Such models are often referred to as being
kinematic
—the motion (as opposed to the “forces” behind
that motion) is of prime consideration. By contrast, car-following models are
dynamic
in the sense that accelerations and decelerations (and by implication, the forces) are implicit in their description. Although it is outside the scope of this book, it is perhaps worth mentioning that the discrete approach is often used to model flocking in starlings, shoaling in fish, and other swarming behavior (in ant, bee, and locust populations, for example).
One very interesting feature common to both natural and man-made phenomena is the topic of stability vs. instability. Will those waves on the lake grow or die out? Will that crack in the windshield continue to grow or stop? (Almost certainly the former!) Will that traffic bottleneck disappear by the time I get there, or will it get worse? A typical traffic “instability” arises from time lags in the response of a driver to the accelerations and decelerations of the vehicle in front. A small lag can grow as it passes, in a wavelike manner from car to car. Indeed, it is accurate to say that terms like “shock wave” and “expanding wave” are quite appropriate to describe some traffic patterns. Typically the existence of such waves in traffic flow can be deduced from both kinematic (continuous fluid-like) models and discrete (“particle”) car-following models. Most are too detailed for inclusion here, but we can gain some insight into these phenomena by examining some simple “steady-state” models. In this context, the steady state represents an equilibrium or perhaps a neutrally stable solution, much like a ball on a flat table—if disturbed, it will not move away indefinitely (instability) or return to its starting point (stability) but will remain where it is placed. This is neutral stability. But we start with an introduction to the probabilistic approach to traffic flow. And as pedestrians, we should be particularly interested in the
gaps
between the vehicles! We shall think about the gaps in what follows.
=
Pr
: PROBABILITY IN THE CITY
Probabilistic (or stochastic) models incorporate, by definition, an element of randomness. This word is not to be understood in the common sense as haphazard; a more precise definition is given below. In this context it can mean that there is a probability distribution for, say, the size of gaps in a line of traffic. We can view traffic or the gaps in traffic as a distribution in space or time. In space, a length of single lane road (for simplicity) will have a distribution of vehicles along it at any given moment in time—a snapshot view. Alternatively we may identify a fixed location on the road with vehicles passing this position
as time goes on. The first situation is a distribution of intervals in space, and the second is a distribution in time. Such distributions (or series of events) are termed
random
provided that [
19
]
(i) each event (e.g., vehicle arrival time) is independent of any other, and
(ii) equal intervals of time (or space) are equally likely to contain equal numbers of events (e.g., vehicles).
There are several important distributions of interest in traffic flow studies; we shall briefly examine two of them—the
Poisson
and (displaced)
negative exponential distributions
. The latter is a simple generalization of a negative exponential distribution. The former gives the probability of a specified number of vehicles along a section of road at a given time, or passing a given point in a certain time interval. The latter provides the probability of a time or distance “gap” of a specified length in a specified time or distance. More precisely, it describes the time between events in a
Poisson process
, that is, a process in which events occur continuously and independently at a constant average rate. A derivation of the Poisson distribution is given in
Appendix 4
.
=
P
(
t
): TRAFFIC GAPS IN THE CITY?
This is an important question that has direct relevance to a topic mentioned above: pedestrians crossing roads. When I walk to work I have several roads to cross, and not all of them have crosswalks. There have also been quite a few occasions when I am in the middle of a crosswalk and cars go right by me (once it was a police cruiser that nearly knocked me down). There is a flavor of probability theory in this chapter, but not to worry, the applications we’ll be making are very straightforward.
We’ll call
P
(
t
) the probability that no vehicle passes a certain point in a time interval
t
. Suppose that, over another period of time
T
a large number
N
of cars pass that same point. What do we mean by large in this context? Let’s take
N
> 100. The average number of cars in a time interval
t
is then
n
=
Nt
/
T
. For events that are equally likely to occur at any time, the distribution of times between the events is well described
exponential distribution
. For example, it is often used for modeling the behavior of items with a constant failure rate.
It also has the advantage of taking a simple mathematical form. We define the exponential distribution

P
(
t
) also describes the probability that there is a gap of at least
t
seconds between the passage of any two consecutive vehicles. Therefore for
N
cars the average number of gaps ≥
t
is given by
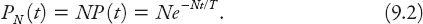
An old survey [
19
] (see Gerlough 1955) of traffic gaps in the Pasadena (Arroyo Seco) Freeway over a period of 1753 seconds (!) in one lane found that 214 cars passed the observation point. By fitting a curve to the experimental data, that is, a plot of the number of gaps of length
L
or greater vs. the length of the gaps, the traffic researchers found quite good agreement between the data and the curve predicted by equation (9.2), namely