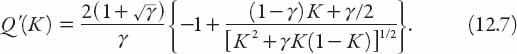X and the City: Modeling Aspects of Urban Life (34 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

=
Q
: ALTERNATIVE CAR-FOLLOWING MODELS
We now consider a driver traveling at speed
u
who tries to maintain a constant distance between his car and the one ahead of him. Since he will wish to be able to stop suddenly if the vehicle ahead does, and to do so without hitting it, the spacing
s
can be written (in particular) as a quadratic function of speed. (Why is this so?) Consider the expression

From equation (12.1) the constants
s
0
,
a
, and
b
must have dimensions of distance, time, and (acceleration)
−1
, respectively. Therefore
s
0
might be, for instance, the minimum spacing from the back of car
n
to the front of the following car (
n
− 1) or front to front. The constant
a
could be the reaction time to a sudden braking of the car ahead, and
b
could be the maximum deceleration, which would modify the speed
u
in order to keep
s
constant. We can solve equation (12.1) for
u
:
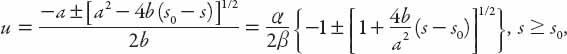
where
α
=
a/s
0
and
β
=
b/s
0
. The positive solution (+ root) can be recast directly into a form related to
q
=
q
(
k
) by defining some new parameters:
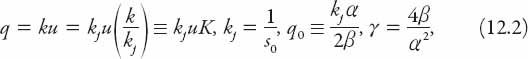
from which we obtain the expression

In view of the above discussion about the shape of the
q
(
k
) (and now the
q
(
K
)) graph, we seek the location of the maximum from
dq
/
dK
= 0, that is, where
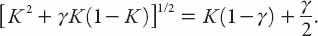
Simplifying, we obtain the following quadratic equation in
K
:
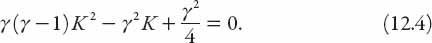
This equation has the roots
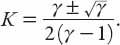
On substituting these into equation (12.3) it transpires that only the – root gives
q
> 0. We can write this value as
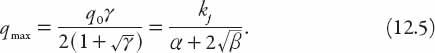
Finally, writing
Q
=
q
/
q
max
we have an expression for
Q
(
K
), that is,
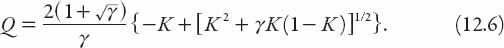
A typical graph of
Q
(
K
) is shown in
Figure 12.1
. The maximum occurs at
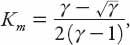
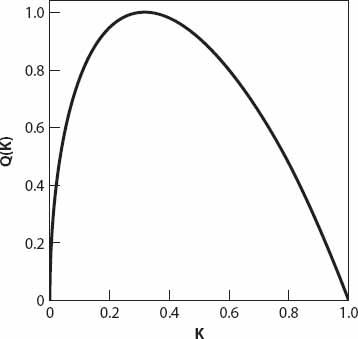
Figure 12.1. Modified
q-k
diagram based on equation (12.6).
The position of the maximum changes relatively little with
γ
; in the interval 1 <
γ
< ∞, for example, 0.25 <
K
m
< 0.5.
Note also that