XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition (487 page)
Read XSLT 2.0 and XPath 2.0 Programmer's Reference, 4th Edition Online
Authors: Michael Kay

An Algorithm for Matching Patterns
This means there is a theoretical algorithm for testing whether a given node
N
matches a pattern
P
, as follows: for each node, starting from
N
and working through its ancestors up to the root node, evaluate
P
as an XPath expression with that node as the context node. If the result is a sequence of nodes containing
N
, the pattern matches; otherwise, keep trying until you get to the root.
XSLT processors don't usually use this algorithm, it's there only as a way of stating the formal rules. The processor will usually be able to find a faster way of doing the test—which is just as well, since pattern matching would otherwise be prohibitively expensive.
Although the formal rules usually give the answer you would expect intuitively, there can be surprises. For example, you might expect the pattern node()
node()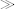 to match any node; but it doesn't. The equivalent expression,
to match any node; but it doesn't. The equivalent expression, //(node())
//(node())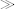 is short for
is short for root(.)/descendant-or-self::node()/child:: node()
root(.)/descendant-or-self::node()/child:: node()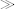 , and the only nodes that this can select are nodes that are children of something. Because document nodes, attribute nodes, and namespace nodes are never children of another node (see the description of the tree model on page 45 in Chapter 2), they will never be matched by the pattern
, and the only nodes that this can select are nodes that are children of something. Because document nodes, attribute nodes, and namespace nodes are never children of another node (see the description of the tree model on page 45 in Chapter 2), they will never be matched by the pattern node()
node()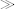 .
.
Patterns Containing Predicates
The formal equivalence of patterns and expressions becomes critical when considering the meaning of predicates (conditions in square brackets), especially predicates that explicitly or implicitly use the
position()
and
last()
functions.
For example, the pattern para[1]
para[1]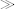 corresponds to the expression
corresponds to the expression root(.)//(para [position() = 1])
root(.)//(para [position() = 1])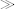 . This expression takes all the
. This expression takes all the para[1]
para[1]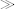 matches any
matches any *[1][self::para]
*[1][self::para]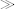 matches any element that is the first child of its parent and that is also a
matches any element that is the first child of its parent and that is also a para[last()! = 1]
para[last()! = 1] matches any
matches any