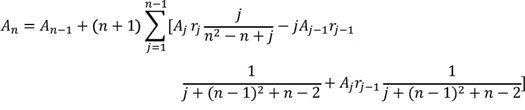Antifragile: Things That Gain from Disorder (87 page)

Increase of risk upon being provided numbers:
See the literature on anchoring (reviewed in
The Black Swan
). Also Mary Kate Stimmler’s doctoral thesis at Berkeley (2012), courtesy Phil Tetlock.

Stimmler’s experiment is as follows. In the simple condition, subjects were told:

For your reference, you have been provided with the following formula for calculating the total amount of money (
T
) the investment will make three months after the initial investment (
I
) given the rate of return (
R
):

T=I*R

 

In the complex condition, subjects were told:

For your reference, you have been provided with the following formula for calculating the total amount of money
A
_n
the investment will make three months after the initial investment
A
_n-1
given the rate of return
r
.

 

Needless to mention that the simple condition and the complex one produced the same output. But those who had the complex condition took more risks.

The delusion of probabilistic measurement:
Something that is obvious to cabdrivers and grandmothers disappears inside university hallways. In his book
The Measure of Reality
(Crosby, 1997), the historian Alfred Crosby presented the following thesis: what distinguished Western Europe from the rest of the world is obsession with measurement, the transformation of the qualitative into the quantitative. (This is not strictly true, the ancients were also obsessed with measurements, but they did not have the Arabic numerals to do proper calculations.) His idea was that we learned to be precise about things—and that was the precursor of the scientific revolution. He cites the first mechanical clock (which quantized time), marine charts and perspective painting (which quantized space), and double-entry bookkeeping (which quantized financial accounts). The obsession with measurement started with the right places, and progressively invaded the wrong ones.
    Now our problem is that such measurement started to be applied to elements that have a high measurement error—in some case infinitely high. (Recall Fukushima in the previous section.) Errors from Mediocristan are inconsequential, those from Extremistan are acute. When measurement errors are prohibitively large, we should not be using the word “measure.” Clearly I can “measure” the table on which I am writing these lines. I can “measure” the temperature. But I cannot “measure” future risks. Nor can I “measure” probability—unlike this table it cannot lend itself to our investigation. This is at best a speculative estimation of something that
can
happen.
    Note that Hacking (2006) does not for a single second consider fat tails! Same with Hald (1998, 2003), von Plato (1994), Salsburg (2001), and from one who should know better, Stigler (1990). A book that promoted bad risk models, Bernstein (1996). Daston (1988) links probabilistic measurement to the Enlightenment.
    
The idea of probability as a quantitative not a qualitative construct has indeed been plaguing us. And the notion that science
equals
measurement free of error—it is, largely but not in everything—can lead us to all manner of fictions, delusions, and dreams.
    An excellent understanding of probability linked to skepticism: Franklin (2001). Few other philosophers go back to the real problem of probability.

Fourth Quadrant:
See the discussion in
The Black Swan
or paper Taleb (1999).

Nuclear, new risk management:
Private communication, Atlanta, INPO, Nov. 2011.

Anecdotal knowledge and power of evidence:
A reader, Karl Schluze, wrote: “An old teacher and colleague told me (between his sips of bourbon) ‘If you cut off the head of a dog and it barks, you don’t have to repeat the experiment.’ ” Easy to get examples: no lawyer would invoke an “N=1” argument in defense of a person, saying “he only killed once”; nobody considers a plane crash as “anecdotal.”
    I would go further and map disconfirmation as exactly where N=1 is sufficient.
    Sometimes researchers call a result “anecdotal” as a knee-jerk reaction when the result is exactly the reverse. Steven Pinker called John Gray’s pointing out the two world wars as counterevidence to his story of great moderation “anecdotal.” My experience is that social science people rarely know what they are talking about when they talk about “evidence.”

Decision theorists teaching practitioners:
To add more insults to us, decision scientists use the notion of “practical,” an inverse designation. See Hammond, Keeney, and Raiffa (1999) trying to teach us how to make decisions. For a book describing exactly how practitioners don’t act, but how academics think practitioners act: Schon (1983).

The asymmetry between good and bad:
Segnius homines bona quam mala sentiunt
in Livy’s
Annals
(XXX, 21).

Stoics and emotions:
Contradicts common beliefs that Stoicism is about being a vegetable, Graver (2007).

Economic growth was not so fast:
Crafts (1985), Crafts and Harley (1992).

Cheating with the rock star:
Arnavist and Kirkpatrick (2005), Griffith et al. (2002), Townsend et al. (2010).

Simenon:
“Georges Simenon, profession: rentier,” Nicole de Jassy
Le Soir illustré
9 janvier 1958, N° 1333, pp. 8–9, 12.

Dalio:
Bridgewater-Associates-Ray-Dalio-Principles.

Aristotle and his influence:
Rashed (2007), both an Arabist and a Hellenist.

The nobility of failure:
Morris (1975).

Bricolage:
Jacob (1977a, 1977b), Esnault (2001).

Rich getting richer:
On the total wealth for HNWI (High Net Worth Individuals) increasing, see Merrill Lynch data in “World’s wealthiest people now richer than
before the credit crunch,” Jill Treanor,
The Guardian,
June 2012. The next graph shows why it has nothing to do with growth and total wealth formation.

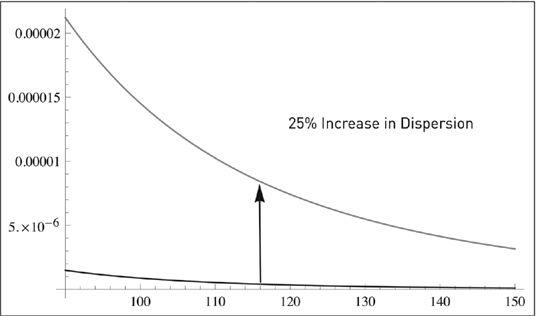
FIGURE 39
.
Luxury goods and optionality. On the vertical the probability, on the horizontal the integral of wealth. Antifragility city: the effect of change in inequality on the pool of very rich increases nonlinearly in the tails: the money of the superrich reacts to inequality rather than total wealth in the world. Their share of wealth multiplies by close to 50 times in response to a change of 25% in dispersion of wealth. A small change of 0.01 in the GINI coefficient (0 when perfect inequality, 1.00 when one person has all) equivalent to 8% rise in real Gross Domestic Product—the effect is stark regardless of the probability distribution.

Camel in Arabia:
Lindsay (2005).

Obliquity:
Kay (2010).

Real options literature:
Trigeorgis (1993), review in Dixit and Pindyck (1994), Trigeorgis (1996), Luehrman (1998), McGrath (1999)—the focus is on reversible and irreversible investments.

Translational gap:
Wooton (2007); Arikha (2008b); modern Contopoulos-Ioannidis et al. (2003, 2008), commentary Bosco and Watts (2007).

Criticism of Wootton:
Brosco and Watts (2007).

Epiphenomena and Granger-causality:
See Granger (1999) for a review.

Lecturing birds how to fly:
There are antecedents in Erasmus, “teaching fish how to swim.”
Adages,
2519, III, VI, 19.
“Piscem nature doces
I’χθὺν νήχεσθαι διδάσκεις
,
id est piscem nature doces. Perinde est ac si dicas : Doctum doces. Confine illi, quod alibi retulimus :
Δελφἶνα νήχεσθαι διδάσκεις
,
id est Delphinum natare doces.”
The expression was first coined in Haug and Taleb (2010), posted in 2006, leading to a book, Triana (2009). We weren’t aware of the Erasmus imagery, which we would have selected instead.

Education and its effect on growth and wealth:
Pritchett (2001), Wolf (2002), Chang (2011).

Schumpeter’s ideas on destruction for advancement:
Schumpeter (1942). Criticism by Harvard economists about lack of technical approach in McCraw (2007).

Amateurs:
Bryson (2010), Kealey (1996).

Scientific misattribution of the works of Bachelier, Thorpe, and others:
Haug and Taleb (2010). Discussion in Triana (2009, 2011).

Jet engine:
Scranton (2006, 2007, 2009), Gibbert and Scranton (2009).

Busting the episteme theory of cybernetics:
Mindell, 2002. I thank David Edgerton for introducing me to his works.

Cathedrals and theoretical and axiomatic geometry:
Beaujoan (1973, 1991), Portet (2002). Ball (2008) for the history of the construction of Chartres cathedral.

Epistemic base and conflation:
The epistemic base is sort of the
x,
not
f
(
x
). A great way
to see the difference between
x
and
f
(
x
) in technology, offered by Michael Polanyi: one can patent
f
(
x
), a technique, but not
x,
scientific knowledge. In Mokyr (2005).

Epistemic Base:
Mokyr (1999, 2002, 2005, 2009). The biggest problem with Mokyr: not getting
ω
_C
. Further, this notion of the East missing trial and error (also see argument about China): see Tetlock in Tetlock et al. (2009). Mokyr and Meisenzahl have a different spin, with microinventions feeding macroinventions. Still intellectually weak.

Techne-Episteme in economics:
Marglin (1996), but the tradition did not go very far.

Needham’s works on China:
Winchester (2008).

Tenure:
Kealey (1996): “Adam Smith attributed the English professors’ decay to their guaranteed salaries and tenured jobs. (As compared to Scottish Universities.)”

Fideism:
Popkin (2003).

Linear Model:
Edgerton (1996a, 1996b, 2004). Edgerton showed that it was a backward-fit idea, that is, fit to the past. Edgerton also writes: “This profoundly academic-research-oriented model of twentieth-century science is all the more surprising in view of the long tradition of
stressing the non-academic origins of modern science
[emphasis mine], particularly the craft traditions, and the insistence of much history of science, strengthened in the last 20 years, on the significance of industrial contexts for science, from dyeing to brewing to engine making.”

Convexity bias:
It was discovered early in commodity and financial futures; Burghardt and Hoskins (1994), Taleb (1997), Burghardt and Liu (2002), Burghardt and Panos (2001), Kirikos and Novak (1997), Pieterbarg and Renedo (2004). Many people blew up on misunderstanding the effect.

Example of detection and mapping of convexity bias (
ω
_A
), from author’s doctoral thesis:
The method is to find what needs dynamic hedging and dynamic revisions. Among the members of the class of instruments considered that are not options
stricto-sensu
but require dynamic hedging can be rapidly mentioned a broad class of convex instruments: (1) Low coupon long dated bonds. Assume a discrete time framework. Take
B
(
r
,
T
,
C
) the bond maturing period
T,
paying a coupon
C
where
rt
= ∫
rs ds.
We have the convexity
д
²
B
/
дr
²
increasing with
T
and decreasing with
C
. (2) Contracts where the financing is extremely correlated with the price of the Future. (3) Baskets with a geometric feature in its computation. (4) A largely neglected class of assets is the “quanto-defined” contracts (in which the payoff is not in the native currency of the contract), such as the Japanese NIKEI Future where the payoff is in U.S. currency. In short, while a Japanese yen denominated NIKEI contract is linear, a U.S. dollars denominated one is nonlinear and requires dynamic hedging.
    Take at initial time
t
₀
, the final condition
V
(
S,T
)
= S
_T
where
T
is the expiration date. More simply, the security just described is a plain forward, assumed to be linear. There appears to be no Ito term there yet. However should there be an intermediate payoff such that, having an accounting period
i/T,
the variation margin is paid in cash disbursement, some complexity would arise. Assume ∆
(t
_i
)
the changes in the value of the portfolio during period
(t
_i
,t
_i-1
)
, ∆(t
_i
)= (V(S,t
_i
)-V(S, t
_i-1
)). If the variation is to be paid at period
t
_i
, then the operator would have to borrow at the forward rate between periods
t
_i
and
T,
here
r
(
t
_i
,T
). This financing is necessary to make
V
(
S,T
) and
S
_T
comparable in present value. In expectation, we will have to discount the variation using forward cash flow method for the accounting period between
t
_i-1
and
t
_i
. Seen from period
T,
the value of the variation becomes
E
_t
[
exp
[
-r
(
t
_i
,T
)(
T-t
_i
)] ∆(t
_i
)], where
E
_t
is the expectation operator at
time
t
(under, say, the risk-neutral probability measure). Therefore we are delivering at period
T,
in expectation, as seen from period
t
₀
, the expected value of a stream of future variation
E
_t0
[Σ
exp
[-
r
(
t
_i
,
T
)(
T
-
t
_i
)] ∆(
t
_i
)]. However we need to discount to the present using the term rate
r
(
T
). The previous equation becomes
V
(
S,T
)
|
_t=t0
= V
[
S,t
₀
]
+ exp
[
r
(
T
)]
E
_to
[Σ
exp
[-
r
(
t
_i
,
T
)(
T
-
t
_i
)] ∆(
t
_i
)], which will be different from
S
_T
when any of the interest rate forwards is stochastic.
Result
(a polite way to say “theorem”):
When the variances of the forward discount rate r
(
t
_i
,
T
)
and the underlying security S
_T
are strictly positive and the correlation between the two is lower than 1, V
(
S,T
)
|
_t=t0
≠ S
_T
. Proof: by examining the properties of the expectation operator. Therefore:
F
(
S, t
₀
)
= F
(
S,t
₀
+
∆
t
), while a nonlinear instrument will merely satisfy:
E
[
V
(
S,t
₀
)]
=E
[
V
(
S,t
₀
+
∆
t
)].

Critique of Kealey:
Posner (1996).

General History of Technology:
Missing convexity biases, Basalla (1988), Stokes (1997), Geison (1995).

Ideas of innovation:
Berkun (2007), Latour and Woolfar (1996), Khosla (2009), Johnson (2010).

Medical discoveries and absence of causative knowledge:
Morton (2007), Li (2006), Le Fanu (2002), Bohuon and Monneret (2009). Le Fanu (2002): “It is perhaps predictable that doctors and scientists should assume the credit for the ascendency of modern medicine without acknowledging, or indeed recognizing, the mysteries of nature that have played so important a part. Not surprisingly, they came to believe their intellectual contribution to be greater than it really was, and that they understood more than they really did. They failed to acknowledge the overwhelmingly empirical nature of technological and drug innovation, which made possible spectacular breakthroughs in the treatment of disease without the requirement of any profound understanding of its causation or natural history.”

Commerce as convex:
Ridley (2010) has comments on Phoenicians; Aubet (2001).

Pharma’s insider:
La Matina (2009).

Multiplicative side effects:
Underestimation of interactions in Tatonetti et al. (2012): they simply uncovered the side effects of people taking joint drugs together, which effectively swells the side effects (they show something as large as a multiplication of the effect by 4).

Strategic planning:
Starbuck et al. (1992, 2008), Abrahamson and Freedman (2007). The latter is a beautiful ode to disorder and “mess.”

Entrepreneurship:
Elkington and Hartigan (2008).

Harvard Business School professors’ pathological misunderstanding of small probabilities:
This is not an empirical statement, but just to have fun: for an illustrative example of a sucker who misses
ω
_B
and
ω
_C
, always start looking in Harvard. Froot (2001), Pisano (2006a, 2006b). Froot: “Because managers of insurance companies purchase reinsurance at far above the fair price, they must believe that risk management adds considerable value.” He thinks
he
knows the fair price.

Le Goff:
Le Goff (1985):
“L’un est un professeur, saisi dans son enseignement, entouré d’élèves, assiégé par les bans, où se presse l’auditoire. L’autre est un savant solitaire, dans son cabinet tranquille, à l’aise au milieu de la pièce où se meuvent librement ses pensées. Ici c’est le tumulte des écoles, la poussière des salles, l’indifférence au décor du labeur collectif,” “Là tout n’est qu’ordre et beauté / Luxe, calme, et volupté.”

Martignon:
Geschlechtsspezifische Unterschiede im Gehirn und mögliche Auswirkungen auf den Mathematikunterricht.
Wissenschaftliche Hausarbeit zur Ersten
Staatsprüfung für das Lehramt an Realschulen nach der RPO I v. 16.12.1999. Vorgelegt von: Ulmer, Birgit. Erste Staatsprüfung im Anschluss an das Wintersemester 2004/05, Pädagogische Hochschule Ludwigsburg. Studienfach: Mathematik. Dozenten: Prof. Dr. Laura Martignon, Prof. Dr. Otto Ungerer.

Renan:
Averroès et l’averroïsme,
p. 323 (1852).

Socrates:
Conversation with Mark Vernon (Vernon, 2009), who believes that Socrates was more like Fat Tony. Wakefield (2009) a great context. Calder et al. (2002) presents portraits more or less hagiographic.

Socratic Fallacy:
Geach (1966).

Episteme
-
Techne
:
Alexander of Aphrodisias,
On Aristotle’s Metaphysics, On Aristotle’s Prior Analytics
1.1–7,
On Aristotle’s Topics
1,
Quaestiones
2.16–3.15.