Arrival of the Fittest: Solving Evolution's Greatest Puzzle (13 page)
Read Arrival of the Fittest: Solving Evolution's Greatest Puzzle Online
Authors: Andreas Wagner

We would then move on to another biomass molecule, perhaps another amino acid, or one of the four DNA building blocks, repeating the entire procedure for each of the building blocks to find out whether the metabolism can manufacture it. Only when
all
essential biomass molecules can be produced is it viable.
32
All of this is done on computers, because computation—done right—is faster, cheaper, and can even be better than experimentation. But as the saying goes, the map is not the territory, and we biologists do not fully trust any computation until we can check it. So like a factory that spot-checks its output randomly, we expose organisms with known metabolic genotypes to known chemical environments, and wait, somewhat ghoulishly, for them to grow or die. This has been done, for example, to several hundred mutant
E. coli
strains, each of them engineered to lack one enzyme, and it shows that their computed viability is highly accurate—it is correct for more than 90 percent of strains.
33
Most biologists who know about this computation think of it as ordinary and do not dwell on how remarkable it is. But more than just remarkable, the capacity to compute viability is profound and revolutionary, a legacy of a hundred years of research in biology and computer science. Darwin and generations of biologists after him could not even dream of it, yet it is crucial to understanding metabolic innovability—nature’s ability to create new metabolic phenotypes.
This computation works for any organism whose metabolism we know, and for any known chemical environment, whether Arctic soil, tropical rain forest, oceanic abyss, or a mountain meadow. It also applies to any aspect of a metabolic phenotype—to any molecule a metabolism
could
make. But among all these aspects, viability is the most fundamental, and new methods of making biomass and using chemical fuels are by far the most important innovations. They are also the most far-reaching, opening new territories to life and its metabolic engines.
The reason for the importance of fuel innovations is simple: The world changes all the time, and no matter how successful a metabolism is
today,
it will almost certainly become unsuccessful at some point in the future, like an economy that depends on exhaustible fossil fuels. Chemical environments always change as consumed nutrients ebb and new foods flow. Organisms that depend on a single, specific combination of nutrients are evolutionary dead ends, and ongoing innovation is needed to survive.
34
Fortunately, many different kinds of molecules
can
provide energy and chemical elements like carbon. Some are as familiar as glucose and sucrose, others less so, like the poison pentachlorophenol.
Even a modest number of potential fuel molecules gives rise to an astounding number of fuel combinations on which a metabolism may or may not be viable—an astounding number of metabolic phenotypes. To see how many, imagine a list like that shown in figure 6, comprising a hundred or so potential fuels. Then compute whether the known metabolism of your favorite animal, plant, or bacterium is viable on a specific fuel molecule, such as glucose. If it can synthesize all biomass molecules from the carbon in glucose, write a “1” next to glucose, otherwise write a “0.” Then repeat this computation for the next fuel molecule, the next one after that, and so on, until each fuel has either a “0” or a “1” next to it. Every single “1” in this list means that the metabolism can synthesize the complete suite of biomass molecules from that particular fuel.
The resulting string of a hundred ones and zeroes encapsulates the fuel molecules that a given metabolism can use to sustain life. It is an extremely compact way of summarizing a metabolic phenotype. Metabolic generalists like
E. coli
can survive on dozens of carbon sources, and their phenotype string contains many ones.
35
Metabolic specialists can live on only a few carbon sources, and their phenotypes contain mostly zeroes.
To count how many such phenotypes exist, the different combinations of a hundred-odd fuels on which an organism
could
be viable, we just need to keep in mind that an organism may (1) or may not (0) be able to live on each fuel—these two and no other possibilities exist. To calculate the total number of possible phenotypes, multiply 2 by itself a hundred times, which yields 2
100
. This number is greater than 10
30
, or a 1 with 30 zeroes added, not quite as large as the number of possible metabolisms, but still a very large number, much larger than, say, the number of stars in our galaxy—approximately 10
11
, or 100 billion.
I was not kidding when I told you that phenotypes are more complex than the modern synthesis would have you believe.
This huge number of phenotypes implies an equally huge number of metabolic innovations. Figure 7 shows one example. The figure’s left side displays the fuel phenotype of a metabolism that can survive on some carbon sources, but not on ethanol, hence the zero next to ethanol. New genes—acquired through gene transfer or otherwise—can change the genotype that brings forth this phenotype. If this change allows the mutant to metabolize ethanol, we replace the “0” next to ethanol with a “1.” Because every conceivable metabolic innovation can be written like this, by replacing a “0” with a “1” in a metabolic phenotype, there are about as many possible metabolic innovations as there are phenotypes.
36
Designing a space to house the library of all possible metabolisms would be challenging, in part because its volumes exceed the number of hydrogen atoms in the universe. To allow us to find specific volumes fast, the library would also have to be supremely well organized. It would take me only seconds to find my copy of Darwin’s
Origin
in the small library of my office, but searching for any one book while grazing through the stacks of an average university’s library would be a bad idea. And if somebody had reshelved the
Origin
in the wrong place, it might be lost forever. The problem is much worse in a hyperastronomical library. The universal library might well contain the secret to immortality—or at least the perfect recipe for turkey stuffing—yet the library is so large that we would
never
find it unless we knew where to look.
FIGURE 7.
A metabolic innovation
An especially simple way to organize the library is to place the most similar texts next to each other. Human librarians do exactly that when they shelve different editions of the same book together. If the metabolic library were organized along these lines, the most similar texts would be immediate neighbors. But there is a problem: To buy or build shelving for this library would be a real pain.
In a human library, every book has two immediate neighbors, one to the left and one to the right, or maximally four, if you want to count the volumes on the shelf above and below as well. How many neighbors would any one text in the metabolic library have? Recall that a string of five-thousand-odd ones and zeroes describes a metabolic genotype. Any neighbor would differ in exactly one of these letters, one chemical reaction that may be either present or absent. (It cannot possibly differ in less than that, and if it differed in more, it would no longer be a neighbor.) There is one neighbor that differs in the first letter of this string, another that differs in the second letter, one that differs in the third letter, and so on, until the very last of these letters. In other words, each metabolic text has not two, not four, but thousands of neighbors, as many as there are biochemical reactions, each of these neighbors differing in a single letter and reaction. Shelves that can hold this sort of inventory aren’t easy to find.
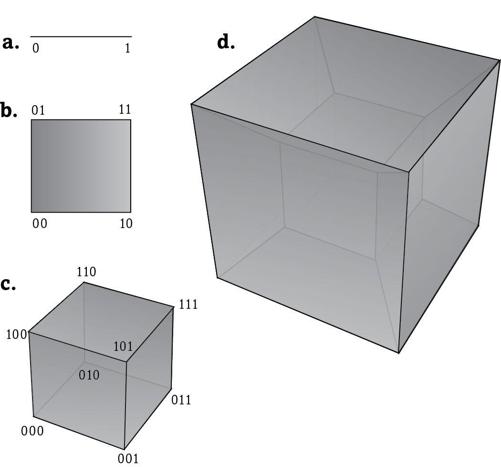
To see how peculiar they would have to be, imagine a much simpler world than ours, the simplest possible chemical world with only one chemical reaction. In this world the metabolic library has only two texts. One of them consists of the letter 1, containing the one and only reaction, the other of the letter 0—it lacks this reaction. Figure 8a shows these texts as the endpoints of a straight line.
A slightly larger universe with two reactions would be big enough for 2 × 2 = 4 possible metabolic texts. One of them has both of these reactions (11), two of them have one reaction but not the other (10, 01), and the fourth metabolism has no reaction (00). Figure 8b shows these metabolisms as the corners of a square.
You may already see where this is going. The next larger reaction universe would have three reactions and 2 × 2 × 2 = 8 possible metabolisms that form the corners of a cube (figure 8c). For a universe with four reactions, we have 2 × 2 × 2 × 2 = 16 possible metabolisms. But which geometric object would correspond to it? As our reaction universe increased from one to two to three reactions, its metabolic texts occupied the endpoints of a line, a square, or a cube, which exist in a one-, two-, and three-dimensional space. Taking it one step further, we need an object in a four-dimensional space. Spaces with four or more dimensions are hard to visualize, but mathematicians routinely work with them, because we can extend our geometrical laws to them.
37
Just as in a square and a cube, the edges of the object we are looking for have to be equally long, and adjacent edges would have right angles to one another. Such an object is a four-dimensional
hypercube
. Figure 8d uses a geometric trick to show this hypercube on paper. It has sixteen corners, each one corresponding to one metabolic text—from 0000 to 1111—that is no longer shown in the figure.
FIGURE 8.
Hypercubes
This trick no longer works in five dimensions, much less higher ones. But although it is hopeless to imagine higher-dimensional spaces, they follow the same laws as our three-dimensional space: The edges of a hypercube are equally long, adjacent edges are at right angles to one another, and each corner corresponds to a possible metabolism. And such cubes in high-dimensional space turn out to have curious properties well suited to house the metabolic library.
The number of corners in a square is four, in a cube it doubles to eight, and in a four-dimensional hypercube it doubles again to sixteen. With every added dimension, it doubles, and by the time you have reached 5,000 dimensions, this number has become the hyperastronomical 2
5000
, the size of the metabolic library. In other words, we can arrange the library’s metabolic texts on the corners of a hypercube in a 5,000-dimensional space. This is why off-the-shelf shelving would not work. You cannot cram the metabolic library into three puny dimensions. It needs thousands of dimensions to breathe.