Beyond the God Particle (33 page)
Read Beyond the God Particle Online
Authors: Leon M. Lederman,Christopher T. Hill
Tags: #Science, #Cosmology, #History, #Physics, #Nuclear, #General

With the details of beta decay now somewhat better understood, and Pauli's hypothesis of the neutrino, Enrico Fermi was able to write down the first mathematically descriptive quantum theory of the “weak interactions” in 1935. Fermi had to introduce a new fundamental constant into physics to specify the overall strength of the weak interactions, much like Newton had to introduce the “gravitational constant.” In fact, Fermi's constant, called G
F
, contains a fundamental unit of mass, which sets the scale of the weak forces—about 175 GeV. With Fermi's theory in hand it was now obvious that high-energy particle accelerators would eventually have to take over to study the details of the weak interactions. And not surprisingly, the Higgs boson has shown up with a mass of 126 GeV, not far from Fermi's “weak scale.”
13
Pauli's neutrinos have also now been produced and subsequently detected in many experiments. Neutrinos were first directly detected by Clyde Cowan and Frederick Reines in 1956.
14
The neutrinos
are important to us—they are emitted from the sun as part of the fusion process by which the sun shines. Our very existence depends critically upon the feeble weak interactions in nature.
THEY DID IT WITHOUT COLLIDERS?
Everything we have discussed to this point represents a fabric of some of the richest scientific discoveries in history—
and none of it was done with high-energy particle colliders!
Nature did all the work for us—it gave us unstable radioactive nuclei and cosmic rays as sources. The physics of beta decay led us to the discovery of the weak interactions and was all done in comparatively “low-energy” experiments, where nature furnished us with a “rare process.” By patiently studying the details of matter, we could infer the deeper structure of nature that is the weak interactions.
Fermi's summation of the weak forces in his theory shows how the relevant high-energy scale of 175 GeV (or equivalent short-distance scale of about 1/10,000,000,000,000,000 centimeters) could be anticipated as early as 1935. It would be 25 years until Glashow would propose the W
+
, W
–
, and Z
0
bosons in the context of the symmetries of the Standard Model, and until Weinberg would show how a Higgs boson could break those symmetries. The actual structure of the weak interactions was not probed directly by colliders until the discovery of the W and Z bosons at CERN in 1985, and of the Higgs boson of 2012. So, from Becquerel to the Higgs boson discovery at CERN, the weak interactions have been at the core of physics research for almost 120 years.
What we have learned is that many of the great scientific advances in the twentieth century came by looking at the details of rare processes. Particle accelerators are generally either the colliders, operating at the highest energies, or smaller machines that produce many collisions, but each at a lower energy. Both offer pathways to discoveries.
For example, we now know that there are three different kinds, or “flavors,” of neutrinos (see
Appendix
). Leon Lederman, Mel Schwartz, and Jack Steinberger demonstrated this in 1962 at the Brookhaven National Laboratory in Upton, New York, using a particle accelerator that provided a secondary beam of muons. With enough muon decays they showed that
neutrinos are produced with distinct identities, by detecting the “
muon-neutrino
,” which is a different particle than the “
electron-neutrino
.” The key to the success of such an experiment is to have a very large number of particles available or a high statistics experiment. This required an
intense source
of sufficiently energetic protons to make muons, but not necessarily a very high-energy collider. With the subsequent discovery of the tau lepton, we now know there are three distinct “flavors” of neutrino.”
15
THE RARE WEAK PROCESSES
Let's isolate the process of beta decay and examine it in greater detail:
At the level of quarks and leptons, the decay of the neutron, if viewed under an extremely powerful microscope, resolves into an individual “down” quark decaying to an “up” quark plus the emission of a W
–
boson. However, the W
–
boson is so heavy that this process can only happen by way of Heisenberg's uncertainty principle for a miniscule moment in time, allowing the energy to fluctuate by a large amount. The W
–
then quickly converts into an electron plus a neutrino (see
fig. 9.34
). It is this extreme mass of the W
–
that makes a weak interaction process very feeble, relying on the big quantum fluctuation in time and energy. The heaviness of the weak gauge boson is, in short, why the weak forces are weak.
This is the defining property of a “rare process.” Rare processes involve something at very short distances over very short time intervals and occurring as a “quantum fluctuation.” Becquerel couldn't observe the W
–
boson directly in a radioactive beta decay, but by measuring beta decay in detail we could later theoretically infer its existence. With Fermi's theory we could actually infer the scale of weak interactions, of 175 GeV, and eventually write down a more precise theory, called the Standard Model, which told the future collider physicists exactly where to look. Physics is like the game “Clue” (also known as “Cluedo”). With enough indirect evidence from rare processes we could say, “It was Colonel Mustard in the Library with the lead pipe” who did it!”
16
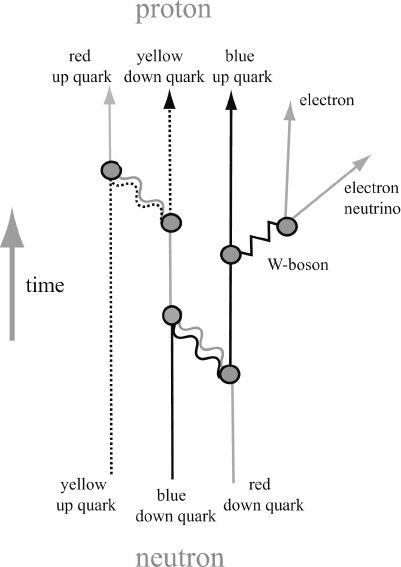
FIGURE 9.34. Beta Decay at Quark Level.
At the level of quarks and leptons, and gluons binding the quarks inside the neutron and proton, we glimpse the process of a neutron decay,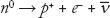 , which involves the quark transition,
, which involves the quark transition,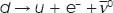 through the exchange of a W boson. The W is so heavy that it is not produced as a real particle, but it is created for only a tiny instant of time (we call it a “virtual particle”), allowed in quantum theory by Heisenberg's uncertainty principle. The improbable quantum fluctuation makes the weak force very “weak.” A free neutron has a half-life of about 11 minutes.
through the exchange of a W boson. The W is so heavy that it is not produced as a real particle, but it is created for only a tiny instant of time (we call it a “virtual particle”), allowed in quantum theory by Heisenberg's uncertainty principle. The improbable quantum fluctuation makes the weak force very “weak.” A free neutron has a half-life of about 11 minutes.
There are a vast number of rare processes that are part of the Standard Model. Many of these have not yet been seen yet in experiments because they are so difficult to observe. And many rare processes are suggested by theories that attempt to go beyond the Standard Model. These effects can show up in two ways, either as inconsistencies in the rates for certain rare process or as tiny effects that are forbidden by the Standard Model. What other tales might rare processes tell us about nature?
THE OTHER LOOKING GLASSES
As we've seen, until the mid-1950s, physicists believed that parity was an exact symmetry of physics. Thus, the world of Alice through the looking glass would be indistinguishable in any physical process from our own world. The question of parity (P) nonconservation in the weak interactions was first raised by two young theorists, T. D. Lee and C. N. Yang, in 1956.
17
Parity symmetry was practically considered to be an obvious fact in nature and had been used for decades in compiling data on nuclear and atomic physics. The breakthrough of Lee and Yang was the idea that the reflection symmetry—parity—could be perfectly respected in most of the interactions that physicists encountered, such as the strong force that holds the atomic nucleus together and the electromagnetic forces together with gravity. But Lee and Yang proposed that the weak force, with its particular form of beta-decay radioactivity, might not possess this mirror symmetry.
Indeed, as we've seen, parity violation was discovered experimentally in 1957 by studying the pion and muon weak-interaction decay in detail. Independently, the effect was seen by Madame Chien-Shiung Wu, using another technique in nuclear weak-decay processes. This was astounding news—the weak processes are not invariant under the parity (P) symmetry operation. Later it was shown that the parity violation of the weak interactions is a property of the fact that only L-handed particles participate in weak interactions, while their R-handed brethren do not. This in turn ultimately mandates the existence of the Higgs boson so that particles can march L-R-L-R through space-time and thus acquire mass.
Let us think a little more about space and time symmetries. Think about viewing the laws of physics by watching a movie. Parity symmetry
would say that you cannot tell if the movie was taken by the camera looking directly at the scene or by viewing the scene reflected though a mirror. For example, the weak decay of a pion or a muon would not appear to us to be consistent with our known laws of physics if the camera is viewing things as a reflection in a mirror. L is exchanged with R, and we would see only R particles participating in the weak interactions in the mirror, not our world, where only L particles do.
But now let's try something different. Let's run the film backward through the projector. This is easy to do with a DVD player nowadays by pressing the “reverse” button. We have all seen, with amusement, the pie fly off Uncle Bert's face or brick towers
un-collapsing
and jumping back into their original positions. Unlike the world viewed through the mirror, it seems very easy to proclaim that you're watching a film that is running backward through the projector. We can therefore imagine a new kind of Alice mirror, a kind of “time looking glass” or “time mirror,” in which we are always viewing things moving backward in time. Alice would find the world through the time mirror apparently quite different than her own. We'll call it “T.”
However, when we examine up close simple or fundamental systems in the time mirror, such as two billiard balls colliding on the pool table, it becomes harder to tell in which direction in time the movie is progressing. The motion we see, forward or backward, viewed through the time mirror, as two billiard balls approach and bounce off one another recoiling into different directions on the table, appears not much changed. It's hard to tell if we're looking through the time mirror, T, or not. The forward-in-time collision on our side of the time mirror seems to respect the same microscopic laws of motion as the backward-in-time collision on the other side of the time mirror. The microscopic laws of motion of simple systems are evidently the same, whether they are run forward or backward in time.
18