Birth of a Theorem: A Mathematical Adventure (33 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

One possibility would be to cut the beast in two in the hope of improving our chances of publishing elsewhere, but I cannot bring myself to do such a thing.… So we’re going to sleep on it.
My talks here have gone well so far, but the same questions keep coming up over and over again. I’ve discussed the matter with Jeff Rauch, a leading expert on partial differential equations who has spent a lot of time working in France. Jeff wasn’t shocked by the fact that the result doesn’t hold for infinite time, but he didn’t like the analyticity assumption. There are others, of course, who would like to see it work in infinite time and who don’t mind the assumption. I could tell myself that it’s no big deal; but since I trust Jeff’s judgment, I find his reservations troubling. So this evening I decided to sit down and write out an argument that would convince him that our proof is as fine a thing as human minds can make it, and that very few, if any, improvements are possible. A good bit of work, but it’s as much for my benefit as for his.

Jeff Rauch
The time went by. Sitting on the bed, scribbling away. I couldn’t find a way to convince myself.… And if I can’t find a way to convince myself, there’s very little chance that I’ll have any luck convincing Jeff!!
What if I went astray somehow, if my estimates weren’t precise enough? Here, though, I haven’t lost anything … there, it would
really
be surprising if I got it wrong … here, it’s optimal … and there, well, simplifying can only help—unless I’ve been utterly bewitched.…
Like a cyclist inspecting his chain for a weak link, I carefully went through the proof, checking the soundness of the argument at each step.
And there …
There!
That’s where I may have been too careless! Jesus, how could I have not seen that the modes are diverging—and that my comparison by summation was too rough!?!? If it’s the sup in relation to the sum, obviously I’m going to lose something!! Well, okay, it got swamped by all the technical detail.…
No time for grumbling, I had to work out the implications.
But of course … the modes diverge, the weight shifts, if you put them all together the loss is huge!! That means they’ve got to be kept separate!!!
This was my moment of illumination, the moment when the light bulb went on in my head. I jumped up from the bed and feverishly paced up and down, pencil in one hand, a sheet of paper covered with cabalistic formulas in the other. I kept on staring at them. This time it wasn’t a question of fixing an error; it was a question of improving our results.
How are we going to get from here to there?
I don’t know. But now at last we’re on our way. We’re going to take the whole thing apart and put it back together. We’ve finally figured out how to lay these two infernal objections to rest, once and for all.
* * *
Since
γ
=
1 is the most interesting case, it is tempting to believe that we stumbled on some deep difficulty. But this is a trap: a much more precise estimate can be obtained by
separating modes
and estimating them one by one, rather than seeking an estimate on the whole norm. Namely, if we set
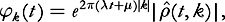
then we have a system of the form

(7.15)
Let us assume that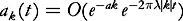 . First we simplify the time dependence by letting
. First we simplify the time dependence by letting
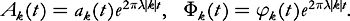
Then (7.15) becomes
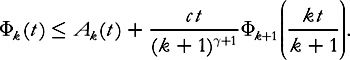
(7.16)
(The exponential for the last term is right because (
k
+
1)(
kt
/(
k
+
1))
=
kt
.) Now if we get a subexponential estimate on
Φ
k
(
t
), this will imply an exponential decay for
ϕ
k
(
t
).
Once again we look for a power series, assuming that
A
k
is constant in time, decaying like
e
−
ak
as
k
→
∞;
so we make the ansatzwith
a
k
,0
=
e
−
ak
.
As an exercise, the reader can work out the doubly recurrent estimate on the coefficients
a
k,m
and deduce
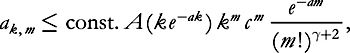
whence
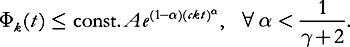
(7.17)
This is subexponential even for
γ
=
1: in fact, we have taken advantage of the fact that
echoes at different values of
k
are asymptotically rather well separated in time
.