Birth of a Theorem: A Mathematical Adventure (35 page)
Read Birth of a Theorem: A Mathematical Adventure Online
Authors: Cédric Villani
Tags: #Non-Fiction, #Science, #Biography

Dear Professor Sjöstrand:
Following your letter of October 23, we are glad to submit a new version of our paper, “On Landau damping,” for possible publication in
Acta Mathematica.
We have taken good note of the concerns expressed by some of the experts in the screening reports on our first submission. We believe that these concerns are fully addressed by the present, notably improved, version.
First, and maybe most importantly, the main result now covers Coulomb and Newton potentials; in an analytic setting this was the only remaining gap in our analysis.
Analyticity is a classical assumption in the study of Landau damping, both in physics and mathematics; it is mandatory for exponential convergence. On the other hand, it is very rigid, and one of the referees complained that our results were tied to analyticity. With this new version this is not so, since we are now able to cover some classes of Gevrey data.
In the first version, we wrote: “[W]e claim that unless some new stability effect is identified, there is no reason to believe in nonlinear Landau damping for, say, gravitational interaction, in any regularity class lower than analytic.” Since then we have identified precisely such an effect (echoes occurring at different frequencies are asymptotically well separated). Exploiting it led to the above-mentioned improvements.
As a corollary, our work now includes new results of stability for homogeneous equilibria of the Vlasov–Poisson equation, such as the stability of certain nonmonotonic distributions in the repulsive case (a longstanding open problem), and stability below the Jeans length in the attractive case.
Another referee expressed a reservation about our use of nonconventional functional spaces. While this may be the case for our “working norm,” it is not so for the naïve norm appearing in our assumptions and conclusions, already used by others. Passing from one norm to another is done by means of Theorem 4.20.
The paper was entirely rewritten to incorporate these improvements, and carefully proofread. To prevent any further increase in the paper’s length, we have cut all expository passages and comments which were not strictly related to our main result; most of the remaining remarks are intended simply to explain the results and methods.
A final comment about length: we are open to discussion regarding adjustments to the organization of the paper, and we note that the modular presentation of the tools used in our work probably makes it possible for some referees to work as a team, thereby hopefully alleviating their task.
We very much hope that this paper will satisfy the experts and remain
Yours truly,
Clément Mouhot & Cédric Villani
* * *

Saint-Rémy-lès-Cheuvreuse
January 7, 2010
Reading email first thing in the morning, as soon as you’ve gotten out of bed, is a sort of intellectual drug injection. Not too much of a jolt, just enough to get you started.
Among the new messages today, Laurent Desvillettes sends unhappy news: our mutual friend Carlo Cercignani has died.
Carlo’s name is inseparable from that of Ludwig Boltzmann. Carlo devoted his professional life to Boltzmann, to Boltzmann’s theories, to his celebrated equation and its many applications. He wrote three of the standard works on Boltzmann, one of them the first research monograph I ever read.
Carlo’s mathematical interests were nevertheless extraordinarily diverse. Boltzmann allowed him to explore a great many topics, some of them having no obvious connection to the equation Carlo so cherished.
And that wasn’t the half of this universal man, polyglot and polymath, highly cultured, who refused to limit himself to the sciences: his works include a play for the theater, a collection of poems, and translations from Homer.
My first important result, or at least the first one I was really proud of, concerned what is known as Cercignani’s conjecture. I was twenty-four years old and raring to go when Giuseppe Toscani invited me to spend two weeks at the University of Pavia in October 1997. An idea had just occurred to Giuseppe about how to tackle this famous conjecture, and he suggested that I give it a go during my brief stay. After a few hours I could see that his crude frontal assault had no chance of success … but I did notice an interesting calculation, something that had the ring of truth about it, the hint of a remarkable new identity. It was all I needed: the mathematical rocket was ready to be launched.
I began by showing that Cercignani’s conjecture regarding entropy production in Boltzmann’s equation could be reduced to an estimate of entropy production in a problem in plasma physics that, as it happened, I had already studied with Laurent. And then I mixed in a bit of information theory, something that has always fascinated me. An incredible combination of circumstances that never would have come about had Giuseppe’s misguided intuition not struck him at precisely the moment I turned up!
Working together, we had
almost
cracked the case by the time I had to leave. Later the same month the opportunity presented itself to announce our results to an audience of the leading experts on the Boltzmann equation at a conference in Toulouse. It was here that Carlo, like many others, first came to know about me. I can still hear the excitement in his voice as he urged me on: “Cédric, prove my conjecture!”
At twenty-four, it was one of my first published articles. Five years later, in my twenty-fourth article, I returned to the problem, only now with more experience and more technique, and succeeded finally in proving Carlo’s brilliant conjecture. He was so proud of me.
The Boltzmann equation still has quite a few loose ends, however, and Carlo was counting on me to tie up some of the most important—and the most maddening—ones. That was one of my ambitions as well. But then, without warning, I wandered off, first in the direction of optimal transport and geometry, then of the Vlasov equation and Landau damping.
I still have it in mind to come back to Boltzmann, just not now. But even if one day my dream comes true, I shall never know the joy of telling Carlo that I’ve tamed his favorite monster, the one he loved before all others.
* * *
Cercignani’s conjecture concerns the relationship between entropy and entropy production in a gas. Let’s simplify, and leave to one side the spatially inhomogeneous character of the gas, so that the only thing that matters is the velocity distribution. Therefore, let f
(
v
)
be a velocity distribution in a gas away from equilibrium:
since this distribution is not equal to the Gaussian
γ
(
v
)
, the entropy is not as high as it might be. Boltzmann’s equation predicts that the entropy will increase. Will it increase by a lot or only by very little?
Cercignani’s conjecture suggests that the instantaneous increase in entropy is at least proportional to the difference between the entropy of the Gaussian and the entropy of the distribution that we’re interested in:
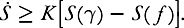
The conjecture has implications for figuring out how fast the distribution converges to equilibrium—a fundamental question connected with Boltzmann’s fascinating discovery of irreversibility.
Laurent Desvillettes worked on Cercignani’s conjecture in the early 1990s, and after him Eric Carlen and Maria Carvalho. They obtained partial results that opened up completely new perspectives, but they were still a long way from proving it. Cercignani himself, with the help of the Russian mathematician Sasha Bobylev, had shown that the conjecture was overly optimistic, that it couldn’t be true … unless perhaps if one were to assume extremely strong collisions, interactions harder than those of so-called hard spheres, with the cross-section increasing at least proportionally to the relative velocity—“very hard spheres,” in the jargon of the kinetic theory of gases.
But in 1997 Giuseppe Toscani and I demonstrated the existence of a bound that is “almost” as good:
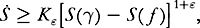
where
ε
is as small as one likes, under certain quite restrictive conditions governing collisions.
In 2003, I showed that this result holds true for all interactions satisfying certain reasonable assumptions; and, more strikingly still, I managed to show that the conjecture is true if the high-velocity collisions are of the very hard sphere type. The key identity, discovered with Toscani six years earlier, was the following:
If
(
S
t
)
t
≥
0
is the semigroup associated with the Fokker–Planck equation, , and
, and then
then