Data Mining (111 page)
Authors: Mehmed Kantardzic

Each chromosome as a potential solution is represented by a concatenation of binary codes for all features in the problem to be optimized. Its total length m is a sum of the features’ code lengths m
i
:
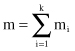
where k is the number of features or input variables for the problem at hand. When we introduce these basic principles of a code construction, it is possible to explain the main steps of a GA.
13.2.1 Encoding Schemes and Initialization
A GA starts with designing a representation of a solution for the given problem. A solution here means any value that is a candidate for a correct solution that can be evaluated. For example, suppose we want to maximize function y = 5 − (x − 1)
2
. Then x = 2 is a solution, x = 2.5 is another solution, and x = 3 is the correct solution of the problem that maximizes y. The representation of each solution for a GA is up to the designer. It depends on what each solution looks like and which solution form will be convenient for applying a GA. The most common representation of a solution is as a string of characters, that is, a string of codes for feature representation, where the characters belong to a fixed alphabet. The larger the alphabet is, the more the information that can be represented by each character in the string is. Therefore, fewer elements in a string are necessary to encode specific amounts of information. However, in most real-world applications, GAs usually use a binary-coding schema.
The encoding process transforms points in a feature space into a bit-string representation. For instance, a point (11, 6, 9) in a three-dimensional (3-D) feature space, with ranges [0, 15] for each dimension, can be represented as a concatenated binary string:
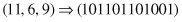
in which each feature’s decimal value is encoded as a gene composed of four bits using a binary coding.
Other encoding schemes, such as Gray coding, can also be used and, when necessary, arrangements can be made for encoding negative, floating-point, or discrete-value numbers. Encoding schemes provide a way of translating problem-specific knowledge directly into the GA framework. This process plays a key role in determining GAs’ performances. Moreover, genetic operators can and should be designed along with the encoding scheme used for a specific application.
A set of all feature values encoded into a bit string represents one chromosome. In GAs we are manipulating not a single chromosome but a set of chromosomes called a population. To initialize a population, we can simply set some
pop-size
number of chromosomes randomly. The size of the population is also one of the most important choices faced by any user of GAs and may be critical in many applications: Will we reach the approximate solution at all, and if yes, how fast? If the population size is too small, the GA may converge too quickly and maybe to a solution that is only the local optimum; if it is too large, the GA may waste computational resources and the waiting time for an improvement might be too long.
13.2.2 Fitness Evaluation
The next step, after creating a population, is to calculate the fitness value of each member in the population because each chromosome is a candidate for an optimal solution. For a maximization problem, the fitness value f
i
of the
i
th member is usually the objective function evaluated at this member (or the point in parameter space). The fitness of a solution is a measure that can be used to compare solutions to determine which is better. The fitness values may be determined from complex analytical formulas, simulation models, or by referring to observations from experiments or real-life problem settings. GAs will work correctly if fitness values are determined appropriately, keeping in mind that a selection of the objective function is highly subjective and problem-dependent.
We usually need fitness values that are positive, so some kind of scaling and/or translation of data may become necessary if the objective function is not strictly positive. Another approach is to use the rankings of members in a population as their fitness values. The advantage of this approach is that the objective function does not need to be accurate, as long as it can provide the correct ranking information.
13.2.3 Selection
In this phase, we have to create a new population from the current generation. The selection operation determines which parent chromosomes participate in producing offspring for the next generation. Usually, members are selected for mating with a selection probability proportional to their fitness values. The most common way to implement this method is to set the selection probability p equal to
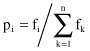
where n is the population size and f
i
is a fitness value for the
i
th chromosome. The effect of this selection method is to allow members with above-average values to reproduce and replace members with below-average fitness values.
For the selection process (selection of a new population with respect to the probability distribution based on fitness values), a roulette wheel with slots sized according to fitness for each chromosome is used. We construct such a roulette wheel as follows:
1.
Calculate the fitness value f(v
i
) for each chromosome v
i
.
2.
Find the total fitness of the population:
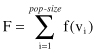
3.
Calculate the probability of a selection p
i
for each chromosome v
i
:
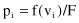
4.
Calculate a cumulative probability q
i
after each chromosome v
i
is included:

where q increases from 0 to maximum 1. Value 1 shows that all chromosomes from the population are included into a cumulative probability.
The selection process is based on spinning the roulette wheel
pop-size
times. Each time, we select a single chromosome for a new population. An implementation could repeat steps 1 and 2
pop-size
times:
1.
Generate a random number r from the range [0, 1].
2.
If r < q
1
, then select the first chromosome v
1
; otherwise, select the
i
th chromosome v
i
such that q
i−1
< r ≤ q
i
.
Obviously, some chromosomes would be selected more than once. That is in accordance with the theory. The GA performs a multidirectional search by maintaining a population of potential solutions and encourages good solutions. The population undergoes a simulated evolution—in each generation the relatively “good” solutions reproduce while the relatively “bad” solutions die. To distinguish between different solutions, we use an objective or evaluation function, which plays the role of an environment.
13.2.4 Crossover
The strength of GAs arises from the structured information exchange of crossover combinations of highly fit individuals. So what we need is a crossover-like operator that would exploit important similarities between chromosomes. The probability of crossover (PC) is the parameter that will define the expected number of chromosomes—PC ·
pop-size
—which undergo the crossover operation. We define the chromosomes for crossover in a current population using the following iterative procedure. Steps 1 and 2 have to be repeated for all chromosomes:
1.
Generate a random number r from the range [0, 1].
2.
If r < PC, select the given chromosome for crossover.
If PC is set to 1, all chromosomes in the population will be included into the crossover operation; if PC = 0.5, only half of the population will perform crossover and the other half will be included into a new population directly without changes.
To exploit the potential of the current gene pool, we use crossover operators to generate new chromosomes that will retain the good features from the previous generation. Crossover is usually applied to selected pairs of parents.
One-point crossover
is the most basic crossover operator, where a crossover point on the genetic code is selected at random, and two parent chromosomes are interchanged at this point. In
two-point crossover
, two points are selected, and a part of chromosome string between these two points is then swapped to generate two children of the new generation. Examples of one- and two-point crossover are shown in Figure
13.1
.