Data Mining (132 page)
Authors: Mehmed Kantardzic

14.8 REVIEW QUESTIONS AND PROBLEMS
1. Find some examples of fuzzy variables in daily life.
2. Show graphically and explain why the law of contradiction is violated in the fuzzy-set theory.
3. The MF of a fuzzy set is defined as
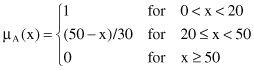
(a)
What will be a linguistic description of the fuzzy set A if x is the variable “age” in years?
(b)
Give an analytical description for μ
B
(x) if B is a fuzzy set “age is close to 60 years.”
4. Assume you were told that the room temperature is around 70 degrees Fahrenheit. How you would represent this information?
(a)
by a set notation,
(b)
by a fuzzy set notation.
5. Consider the fuzzy sets A, B, and C defined on the interval x = [0, 10] with corresponding μ functions:
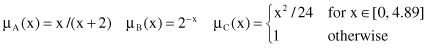
Determine analytically and graphically:
(a)
A′ and B′
(b)
A ∪ C and A ∪ B
(c)
A ∩ C and A ∩ B
(d)
A ∪ B ∪ C
(e)
A ∩ C′
(f)
Calculate the α-cuts for A, B, and C if α = 0.2, α = 0.5, and α = 1.
6. Consider two fuzzy sets with triangular MFs A(x, 1, 2, 3) and B(x, 2, 2, 4). Find their intersection and union graphically, and express them analytically using the min and max operators.
7. If X = {3, 4, 5} and Y = {3, 4, 5, 6, 7}, and the binary fuzzy relation R = “Y is much greater than X” is defined by the analytical MF
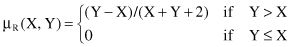
what will be corresponding relation matrix of R (for all discrete X and Y values)?
8. Apply the extension principle to the fuzzy set
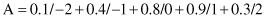
where the mapping function f(x) = x
2
− 3.
(a)
What is the resulting image B where B = f(A)?
(b)
Sketch this transformation graphically.
9. Assume that the proposition “if x is A then y is B” is given where A and B are fuzzy sets:
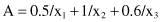
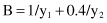
Given a fact expressed by the proposition “x is A*,” where
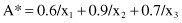
derive the conclusion in the form “y is B*” using the generalized
modus ponens
inference rule.
10. Solve Problem number 9 by using
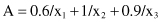
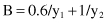
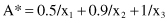
11. The test scores for the three students are given in the following table:
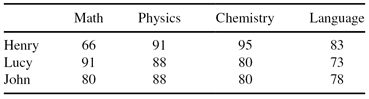
Find the best student using multifactorial evaluation, if the weight factors for the subjects are given as the vector W = [0.3, 0.2, 0.1, 0.4].
12. Search the Web to find the basic characteristics of publicly available or commercial software tools that are based on fuzzy sets and fuzzy logic. Make a report of your search.
14.9 REFERENCES FOR FURTHER STUDY
Chen, Y., T. Wang, B. Wang, Z. Li, A Survey of Fuzzy Decision Tree Classifier,
Fuzzy Information and Engineering
, Vol. 1, No. 2, 2009, pp. 149–159.
Decision-tree algorithm provides one of the most popular methodologies for symbolic knowledge acquisition. The resulting knowledge, a symbolic decision tree along with a simple inference mechanism, has been praised for comprehensibility. The most comprehensible decision trees have been designed for perfect symbolic data. Over the years, additional methodologies have been investigated and proposed to deal with continuous or multi-valued data, and with missing or noisy features. Recently, with the growing popularity of fuzzy representation, some researchers have proposed to utilize fuzzy representation in decision trees to deal with similar situations. This paper presents a survey of current methods for Fuzzy Decision Tree (FDT) designment and the various existing issues. After considering potential advantages of FDT classifiers over traditional decision-tree classifiers, we discuss the subjects of FDT including attribute selection criteria, inference for decision assignment, and stopping criteria.