Data Mining (120 page)
Authors: Mehmed Kantardzic

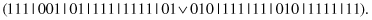
13.6.2 RuleGeneralization
This unary operator generalizes a random subset of complexes. For example, for a parent
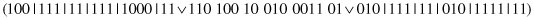
and the second and third complexes selected for generalization, the bits are
OR
ed and the following offspring is produced:
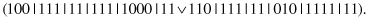
13.6.3 RuleSpecialization
This unary operator specializes a random subset of complexes. For example, for a parent
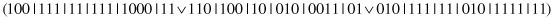
and the second and third complexes selected for specialization, the bits are
AND
ed, and the following offspring is produced:
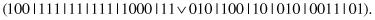
13.6.4 RuleSplit
This operator acts on a single complex, splitting it into a number of complexes. For example, a parent
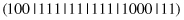

may produce the following offspring (the operator splits the second selector):
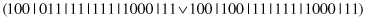
The GIL system is a complex, inductive-learning system based on GA principles. It requires a number of parameters, such as the probabilities of applying each operator. The process is iterative. At each iteration, all chromosomes are evaluated with respect to their completeness, consistency, and fitness criteria, and a new population is formed with those chromosomes that are better and more likely to appear. The operators are applied to the new population, and the cycle is repeated.
13.7 GAS FOR CLUSTERING
Much effort has been undertaken toward applying GAs to provide better solutions than those found by traditional clustering algorithms. The emphasis was on appropriate encoding schemes, specific genetic operators, and corresponding fitness functions. Several encoding schemes have been proposed specifically for data clustering, and the main three types are
binary
,
integer
, and
real encoding
.
The
binary encoding
solution is usually represented as a binary string of length
N
, where
N
is the number of data set samples. Each position of the binary string corresponds to a particular sample. The value of the
i
th gene is 1 if the
i
th sample is a prototype of a cluster, and 0 otherwise. For example, the data set
s
in Table
13.5
can be encoded by means of the string [0100001010], in which samples 2, 7, and 9 are prototypes for clusters C
1
, C
2
, and C
3
. The total number of 1s in the string is equal to an a priori defined number of clusters. Clearly, such an encoding scheme leads to a
medoid-based representation
in which the cluster prototypes coincide with representative samples from the data set. There is an alternative way of representing a data partition using a binary encoding. The matrix of
k
×
N
dimensions is used in which the rows represent clusters, and the columns represent samples. In this case, if the
j
th sample belongs to the
i
th cluster then 1 is assigned to (i,j) genotype, whereas the other elements of the same column receive 0. For example, using this representation, the data set in Table
13.5
would be encoded as 3 × 10 matrix in Table
13.6
.
TABLE 13.5.
Three Clusters Are Defined for a Given Data Set s
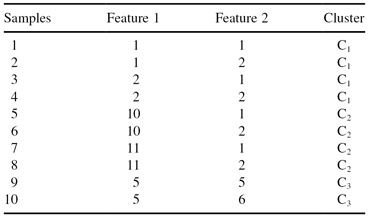
TABLE 13.6.
Binary Encoded Data Set s Given in Table
13.5
