Data Mining (121 page)
Authors: Mehmed Kantardzic

Integer encoding
uses a vector of
N
integer positions, where
N
is the number of data set samples.
Each position corresponds to a particular sample; that is, the
i
th position (gene) represents the
i
th data sample. Assuming that there are
k
clusters, each gene has a value over the alphabet {1, 2, 3, … ,
k
}. These values define the cluster labels. For example, the integer vector [1111222233] represents the clusters depicted in Table
13.5
. Another way of representing a partition by means of an integer-encoding scheme involves using an array of only
k
elements to provide a
medoid-based representation
of the data set. In this case, each array element represents the index of the sample
x
i
,
i
=
1, 2, … ,
N
(with respect to the order the samples appear in the data set) corresponding to the prototype of a given cluster. As an example, the array [1 6 10] may represent a partition in which 1, 6, and 10 are indices of the cluster prototypes (medoids) for the data set in Table
13.5
. Integer encoding is usually more computationally efficient than the binary-encoding schemes.
Real encoding
is the third encoding scheme where the genotypes are made up of real numbers that represent the coordinates of the cluster centroids. In an
n-
dimensional space, the first
n
positions represent the
n
coordinates of the first centroid; the next
n
positions represent the coordinates of the second centroid, and so forth. To illustrate this, the genotype [1.5 1.5 10.5 1.5 5.0 5.5] encodes the three centroids: (1.5, 1.5), (10.5, 1.5), and (5.0, 5.5) of clusters C1, C2, and C3 in Table
13.5
, respectively.
The second important decision, in applying GAs for clustering, is a selection of appropriate
genetic operators
. A number of crossover and mutation operators are proposed trying to solve an important problem of the
context-insensitivity
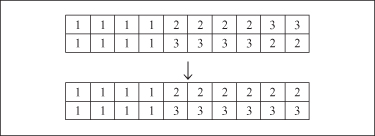
in GAs. When traditional genetic operators are employed in clustering problems, they usually just manipulate gene values without taking into account their connections with other genes. For example, the crossover operation presented in Figure
13.7
shows how two parents representing the same solution to the clustering problem (different labeling but the same integer encoding) produce the resulting offspring representing clustering solutions different from the ones encoded into their parents. Moreover, assuming that the number of clusters has been fixed in advance as
k
= 3, invalid solutions with only two clusters have been derived. Therefore, it is necessary to develop specially designed genetic operators for clustering problems. For example, the crossover operator should be repeatedly applied or randomly scrambling mutation performed until a valid child has been found.
Figure 13.7.
Equal parents produce different offspring through crossover.
Different clustering validity criteria are adapted as
fitness functions
to evolve data partitions in clustering problems. They depend primarily on encoding schemes but also on a selected set of genetic operators. We will illustrate in this text only one example of a clustering fitness function when a
real, centroid-based
encoding scheme is used. Fitness function
f
minimizes the sum of squared Euclidean distances of the samples from their respective cluster means. Formally, the fitness function
f
(C
1
,C
2
, … , C
k
) is:
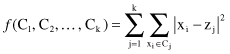
where {C
1
, C
2
, … , C
k
} is the set of
k
clusters encoded into the genotype, x
i
is a sample in a data set, and z
j
is the centroid of cluster C
j
. It is important to stress that this criterion is valid only if the number of clusters
k
is given in advance, and it minimizes the intra-cluster distances and maximizes the intercluster distances as well. In general, fitness functions are based on the distance between samples and either cluster centroids or medoids. Although these types of functions are widely used, usually they are biased toward the discovery of spherical clusters, which clearly will be inappropriate in many real-world applications. Other approaches are possible, including a density-based fitness function. In practice, the success of a GA to solve a clustering problem is highly dependent upon how it has been designed in terms of encoding scheme, operators, fitness function, selection procedure, and initial population generation.
13.8 REVIEW QUESTIONS AND PROBLEMS
1. Given a binary string that represents a concatenation of four attribute values:
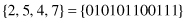
use this example to explain the basic concepts of a GA and their equivalents in natural evolution.
2. If we want to optimize a function f(x) using a GA where the precision requirement for x is six decimal places and the range is [−1, 2], what will be the length of a binary vector (chromosome)?
3. If v1 = (0 0 1 1 0 0 1 1) and v2 = (0 1 0 1 0 1 0 1) are two chromosomes, and suppose that the crossover point is randomly selected after the fifth gene, what are the two resulting offspring?
4. Given the schema (* 1 * 0 0), what are the strings that match with it?
5. What is the number of strings that match with the schema (* * * * * * * *)?
6. The function f(x) = −x
2
+ 16x is defined on interval [0, 63]. Use two iterations of a GA to establish the approximate solution for a maximum of f(x).
7. For the function f(x) given in Problem number 6, compare three schemata
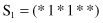
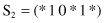
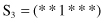
with respect to order (O), length (L), and fitness (F).
8. Given a parent chromosome (1 1 0 0 0 1 0 0 0 1), what is the potential offspring (give examples) if the mutation probability is
(a)
p
m
= 1.0
(b)
p
m
= 0.5
(c)
p
m
= 0.2
(d)
p
m
= 0.1
(e)
p
m
= 0.0001
9. Explain the basic principles of the building-block hypothesis and its potential applications.
10. Perform a PMC operation for two strings S1 and S2, in which two randomly selected crossing points are given: