Data Mining (56 page)

With linear multivariate nodes, we can use hyperplanes for better approximation using fewer nodes. A disadvantage of the technique is that multivariate nodes are mode difficult to interpret. Also, more complex nodes require more data. The earliest version of multivariate trees is implemented in CART algorithm, which fine-tunes the weights w
_i
one by one to decrease impurity. CART also has a preprocessing stage to decrease dimensionality through subset input selection (and therefore reduction of node complexity).

6.7 LIMITATIONS OF DECISION TREES AND DECISION RULES

Decision rule- and decision tree-based models are relatively simple and readable, and their generation is very fast. Unlike many statistical approaches, a logical approach does not depend on assumptions about distribution of attribute values or independence of attributes. Also, this method tends to be more robust across tasks than most other statistical methods. But there are also some disadvantages and limitations of a logical approach, and a data-mining analyst has to be aware of it because the selection of an appropriate methodology is a key step to the success of a data-mining process.

If data samples are represented graphically in an n-dimensional space, where n is the number of attributes, then a logical classifier (decision trees or decision rules) divides the space into regions. Each region is labeled with a corresponding class. An unseen testing sample is then classified by determining the region into which the given point falls. Decision trees are constructed by successive refinement, splitting existing regions into smaller ones that contain highly concentrated points of one class. The number of training cases needed to construct a good classifier is proportional to the number of regions. More complex classifications require more regions that are described with more rules and a tree with higher complexity. All that will require an additional number of training samples to obtain a successful classification.

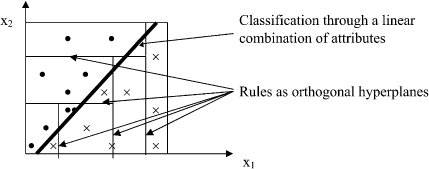
A graphical representation of decision rules is given by orthogonal hyperplanes in an n-dimensional space. The regions for classification are hyperrectangles in the same space. If the problem at hand is such that the classification hyperplanes are not orthogonal, but are defined through a linear (or nonlinear) combination of attributes, such as the example in Figure
6.13
, then that increases the complexity of a rule-based model. A logical approach based on decision rules tries to approximate non-orthogonal, and sometimes, nonlinear classification with hyperrectangles; classification becomes extremely complex with large number of rules and a still larger error.

Figure 6.13.
Approximation of non-orthogonal classification with hyperrectangles.

A possible solution to this problem is an additional iteration of the data-mining process: Returning to the beginning of preprocessing phases, it is necessary to transform input features into new dimensions that are linear (or nonlinear) combinations of initial inputs. This transformation is based on some domain heuristics, and it requires emphasis with additional effort in data preparation; the reward is a simpler classification model with a lower error rate.

The other types of classification problems, where decision rules are not the appropriate tool for modeling, have classification criteria in the form: A given class is supported if n out of m conditions are present. To represent this classifier with rules, it would be necessary to define (
^m
_n
) regions only for one class. Medical diagnostic decisions are a typical example of this kind of classification. If four out of 11 symptoms support diagnosis of a given disease, then the corresponding classifier will generate 330 regions in an 11-dimensional space for positive diagnosis only. That corresponds to 330 decision rules. Therefore, a data-mining analyst has to be very careful in applying the orthogonal-classification methodology of decision rules for this type of nonlinear problems.

Finally, introducing new attributes rather than removing old ones can avoid the sometimes intensive fragmentation of the n-dimensional space by additional rules. Let us analyze a simple example. A classification problem is described by nine binary inputs {A
₁
, A
₂
, … , A
₉
}, and the output class C is specified by the logical relation

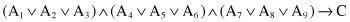
The above expression can be rewritten in a conjunctive form:

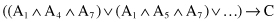
and it will have 27 factors with only ∧ operations. Every one of these factors is a region in a 9-D space and corresponds to one rule. Taking into account regions for negative examples, there exist about 50 leaves in the decision tree (and the same number of rules) describing class C. If new attributes are introduced:

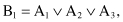
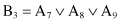
the description of class C will be simplified into the logical rule

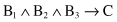
It is possible to specify the correct classification using a decision tree with only four leaves. In a new three-dimensional space (B
₁
, B
₂
, B
₃
) there will be only four decision regions. This kind of simplification via constructive induction (development of new attributes in the preprocessing phase) can be applied also in a case n-of-m attributes’ decision. If none of the previous transformations are found appropriate, the only way to deal with the increased fragmentation of an n-dimensional space is to bring more data to bear on the problem.

6.8 REVIEW QUESTIONS AND PROBLEMS

1.
Explain the differences between the statistical and logical approaches in the construction of a classification model.

2.
What are the new features of C4.5 algorithm comparing with original Quinlan’s ID3 algorithm for decision tree generation?

3.
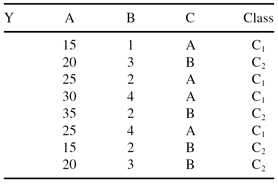
Given a data set X with 3-D categorical samples:

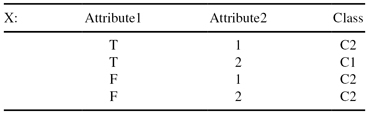
Construct a decision tree using the computation steps given in the C4.5 algorithm.

4.
Given a training data set Y: