Data Mining (69 page)
Authors: Mehmed Kantardzic

The
random subspace method
(RSM) is a relatively recent method of ensemble learning that is based on the theory of stochastic discrimination. Learning machines are trained on randomly chosen subspaces of the original input space and the outputs of the models are then combined. Illustrative example for the classification of movies is given in Figure
8.5
. RSM works well for large feature sets with redundant features. Random forest methodology, which utilizes such an approach, is implemented in many commercial data-mining tools.
Figure 8.5.
RSM approach in ensemble classifier for movie classification.

Methodologies based on different training subsets of input samples (d) are the most popular approaches in ensemble learning, and corresponding techniques such as bagging and boosting are widely applied in different tools. But, before the detailed explanations of these techniques, it is necessary to explain one additional and final step in ensemble learning, and that is combining of outcomes for different learners.
8.2 COMBINATION SCHEMES FOR MULTIPLE LEARNERS
Combination schemes include:
1.
Global approach
is through learners’ fusion where all learners produce an output and these outputs are combined by voting, averaging, or stacking. This represents integration (fusion) functions where for each pattern, all the classifiers contribute to the final decision.
2.
Local approach
is based on learner selection where one or more learners responsible for generating the output are selected based on their closeness to the sample. Selection function is applied where for each pattern, just one classifier, or a subset, is responsible for the final decision.
3.
Multistage combination
uses a serial approach where the next learner is trained with or tested on only instances where previous learners were inaccurate.
Voting
is the simplest way of combining classifiers on a global level, and representing the result as a linear combination of outputs d
j
for
n
learners:
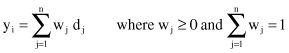
The result of the combination could be different depending on w
j
. Alternatives for combinations are
simple sum (
equal weights
), weighted sum, median, minimum, maximum,
and
product of d
ij
.
Voting schemes can be seen as approximations under a Bayesian framework where weights w
j
approximate prior model probabilities.
Rank-level Fusion Method
is applied for some classifiers that provide class “scores,” or some sort of class probabilities. In general, if Ω = {
c1
, … ,
ck
} is the set of classes, each of these classifiers can provide an “ordered” (ranked) list of class labels. For example, if probabilities of output classes are 0.10, 0.75, and 0.20, corresponding ranks for the classes will be 1, 3, and 2, respectively. The highest rank is given to the class with the highest probability. Let us check an example, where the number of classifiers is N = 3, and the number of classes k = 4, Ω = {
a
,
b
,
c
,
d
}. For a given sample, the ranked outputs of the three classifiers are as follows:
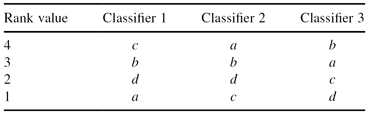
In this case, final selection of the output class will be determined by accumulation of scores for each class:
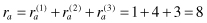
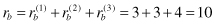

The winner class is
b
because it has the maximum overall rank.
Finally, the
Dynamic Classifier Selection
(DCS) algorithm, representing a local approach, assumes the following steps:
1.
Find the k nearest training samples to the test input.
2.
Look at the accuracies of the base classifiers on these samples.
3.
Choose one (or top N) classifiers that performs best on these samples.
4.
Combine decisions for selected classifiers.
8.3 BAGGING AND BOOSTING
Bagging and boosting are well-known procedures with solid theoretical background. They belong to the class (d) of ensemble methodologies and essentially they are based on resampling of a training data set.
Bagging
, a name derived from bootstrap aggregation, was the first effective method of ensemble learning and is one of the simplest methods. It was originally designed for classification and is usually applied to decision tree models, but it can be used with any type of model for classification or regression. The method uses multiple versions of a training set by using the bootstrap, that is, sampling with replacement. Each of these data sets is used to train a different model. The outputs of the models are combined by averaging (in the case of regression) or voting (in the case of classification) to create a single output.
In the bagging methodology a training data set for a predictive model consists of samples taken with replacement from an initial set of samples according to a sampling distribution. The sampling distribution determines how likely it is that a sample will be selected. For example, when the sampling distribution is predefined as the uniform distribution, all
N
training samples have the same probability, 1/
N
, of being selected. In the same training data set, because of replacement sampling, some training samples may appear multiple times, while any training samples may not appear even once. In Figure
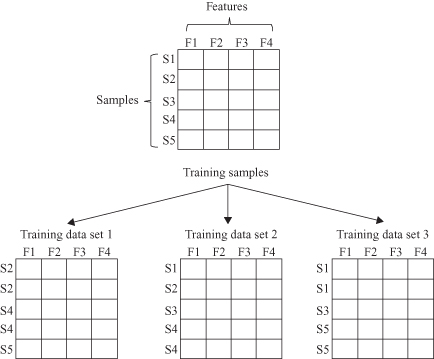
8.6
, there are five training samples {S1, S2, S3, S4, S5} with four features {F1, F2, F3, F4}. Suppose that three training data sets are formed by samples that are randomly selected with replacement from the training samples according to the uniform distribution. Each training sample has a 1/5 probability of being selected as an element of a training data set. In the training data set 1, S2 and S4 appear twice, while S1 and S3 do not appear.
Figure 8.6.
Bagging methodology distributes samples taken with replacement from initial set of samples.
Bagging is only effective when using unstable nonlinear models where small changes in training data lead to significantly different classifiers and large changes in accuracy. It decreases error by decreasing the variance in the results of unstable learners.