Death by Sudoku (24 page)

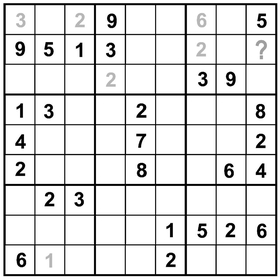
Strangely enough, this is not a form of strip tennis or an offshoot of online dating, but rather another good technique for starting out with a puzzle. Some members of Sudoku Nation call it “counting down.” Choosing a particular space on the puzzle, you ask, “Can a 1 go here? Can a 2?” and so on. It’s best to try this abbreviated form of twenty questions (all right, nine) on a row, column, or box that has the majority of spaces filled. When checking the intersecting rows or columns and the overlapping box for answers to your questions, you’ll have fewer possibilities to begin with.

We’ve progressed a little farther along with this puzzle, as you see. Try the technique on the space marked with the trusty question mark.

When you’ve run through the possibilities, you’re left with only one. Fill it in, and let’s keep going.

This column has always been strictly apolitical, no Republicans or Democrats involved. The only candidates you’ll see here are suggested values for various spaces. Using this technique calls for a sharp pencil to write in small notations for possible values in each box. The way some newspapers shrink their puzzles to almost postage-stamp size, you’re lucky to fill in the actual answers. Many thanks to the
Oregon Daily
for giving us enough space to work in.
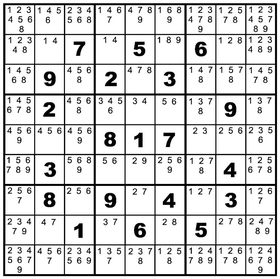Anyhow, here is puzzle two in all its debut splendor, with the candidates for each space in a type size that hopefully won’t cause early blindness.

Yes, it’s tedious, but this is where the real work begins in solving sudoku. Every technique from here on aims at reducing those clumps of candidates to the one true value that must fill a given space. You’ll need sharp eyes as well as a sharp pencil to keep updating the incredible shrinking candidates as they are eliminated either by the appearance of true values or by various techniques along the way.

Finally, a technique I can name without having all of you out there snickering at the implied innuendos. Sudoku techniques can’t all have sexy names. Another way of
looking at this might be “lining up the candidates.” When you were searching for hidden singles, you relied on the interaction between blocks and rows or columns. As you try it, you may find yourself swearing because those interactions lead you to boxes where there are two or three possible spaces for a value, instead of the one you were hoping for. However, frustration in that technique offers the chance for subtraction in this one.

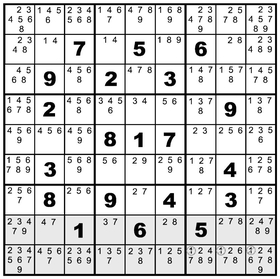
Look at the way the value 1 distributes itself among the left-hand set of vertical boxes. In the bottom box, it’s one of the givens, eliminating any other appearances there and prohibiting 1s in the rest of column three, which is shaded in gray. In the middle box, 1s appear in column one where they’re circled and the column shaded. That means that for the top left box, 1 can only be found in column two, where right now there are two competing spaces.

After eliminating the 1s in the first column of box one, look across on the top tier of boxes. The top two rows of the middle box contain 1s, but not in row three. In fact, the only place where 1s appear in that row now is in the right-hand box. That allows you to eliminate all the 1 candidates in the top two rows of that box as shown in the next diagram.

Look now across the bottom tier of boxes. The left-hand box has a solid value established in the third space of row eight. The middle box has two possible spaces that could have 1s in row nine. That means, by process of elimination, row seven holds the only possible spaces for 1s in the right-hand box. I can see you’re thinking, “Very nice, but is there a point to all of this?”

Here it comes. As this version of the puzzle shows, we can clear away a lot more of the candidate underbrush using this technique. But all the 1s we pruned back created an
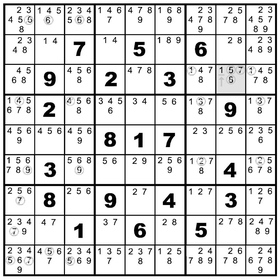
interesting situation in the shaded space in the following diagram. In column eight, we have only a single candidate left for the value of 1—right there in row three. That value gets inked in, two more 1 candidates are removed from the spaces flanking it in the row, and we only have sixty more spaces to fill. Yes, it’s slow. Get used to it.

This is
not
what happens when naked singles get together on the Internet. Naked pairs occur when two spaces in a row, column, or box hold two (and only two) matching candidates. The logic here is pretty straightforward. If spaces three and five offer a choice between 7 and 9, a 7 in space three means a 9 in space five—and vice versa.

There’s a naked pair hanging out shamelessly in row two,
at columns two and four. Since these spaces prohibit any other appearances of 1 and 4, you can eliminate these numbers from the candidate lists in three other spaces, as shown.

If you really want to get kinky, consider the naked triple. This involves three spaces holding pairs of numbers which will eliminate three candidates from a row, column, or box. They’re a bit harder to spot, even though they’re out in plain sight. Resolving the naked pair we just discussed actually helps to create some of this three-way action. We’re going to fast-forward slightly on the puzzle, clearing away a few more candidates. (Trust me, it’s valid. We’ll discuss the technique shortly.)

Look down column six. In the previous puzzle version, we removed a 1 in row two, leaving only 8 and 9 as candidates there. Farther down the column in row six there are a
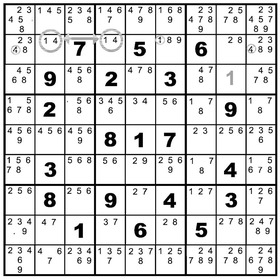2 and 9, while in row eight we find a 2 and an 8. The choices here create a chain of logic that loops between all three locations. An 8 in row two means a 2 in row eight and a 9 in row six. A 9 in row two means a 2 in row six and an 8 in row eight. You can see how one choice forces the others. The chain also forces two candidates out of the clump in column six, row one—as shown below.

No, they’re not carrying on behind everyone’s backs. A hidden pair represents two spaces with the same two candidates—and the same logical consequences as a naked pair. Unfortunately, the pair is hidden among other candidates in the spaces, which makes these guys harder to spot.