Death by Sudoku (25 page)

In the next diagram, look down column one to row four and row six. Together, these two spaces hold ten possible candidates. However, they also represent the only two places where the numbers 1 and 7 appear in that column. So six cluttering candidates get eliminated. There are three other hidden pairs to be found—here are some hints. Look for a 3- 4 pair, a 1-5 pair, and a 2-9 pairing in the rows and columns.

This has nothing to do with
Star Wars
, although there is a force involved—a forcing chain of logic. The basic position to look for is two lines, each sharing the same candidate at the same spaces. These positions would form the corners of a square or rectangle. A perfect example would be two sets of naked pairs that happen to line up.

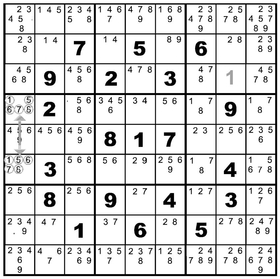
A choice in any corner of this quadrilateral forces a chain reaction among the other corners. Consider what happens if 5 were chosen in the upper left-hand corner:

This possibility prohibits the choice of a 5 in the row across and also in the column down. However, it forces the choice of a 5 in the opposite corner.

Perhaps some arrows will make it clearer.

Put another way, this situation creates a logical chain diagonally across the puzzle. If 5 is chosen in the upper left, it will also appear in the lower right. The opposite is also true—choosing 5 for the upper right forces the choice for 5 in the lower left. The crossing of those diagonal chains of logic creates an X and gives the X-wing its name. It doesn’t just make a pretty pattern, however. Because the given value
must
appear at two corners of the rectangle, it allows you to remove other appearances of the value along the lines making up two of the sides of the
rectangle. In the case illustrated to the left you could remove any other 5s from the far columns making the upright sides of the rectangle, as shown.

Unfortunately, real life is often messier than theory. Look at the rectangle formed from row one, column two, to row one, column eight, to row five, column eight, and back to row five, column two. This is an X-wing for the value 5. Choosing 5 in the upper left prohibits 5s in the upper right and lower left and forces a 5 in the lower right. Or, choosing a 5 in the upper right forces a 5 in the lower left. The point is, this situation allows you to remove six instances of the number 5 from various candidate spaces along rows 1 and 5, as shown. See if you can find a second X-wing in this version of the puzzle. Here’s a hint: look for 6s.

It’s not just the title of a confusing movie, it’s also the name of a confusing logical loop in sudoku. Just as the notion of naked pairs could be stretched to naked triples, the idea of a four-point logical loop from the X-wing can be stretched to six points in swordfish. And, by working along the involved lines, you should be able to eliminate other instances of a particular value.

We’ve fast-forwarded a bit in the puzzle to reach a swordfish situation. The swordfish depends on either/or situations for placing the number 7 in columns two, four, and eight.

As the arrows show, choosing a 7 in column two, row one, prohibits a 7 in column eight, row one. This allows us to place the 7 in column eight, row nine, but prohibits a 7 in column two, row nine. In turn, this forces a 7 at column two, row eight, and prohibits a 7 in column four, row eight. This means that however the choice works out, one of two spaces in rows one, eight, and nine will claim the number 7 and prohibit it anywhere else in those rows. This means that you can eliminate the number 7 from among the candidates in seven other spaces in rows one, eight, and nine. Pretty lucky, huh?

This is not an easy concept to comprehend, and I have seen at least one aspiring sudoku solver asking on the Net for explanation/clarification before his head exploded. This is a chain of logic that, instead of an X-wing rectangle, forms an odd-shaped, six-pointed loop. If it doesn’t come back around to its starting point, it’s not a loop—and you don’t have a swordfish.

When you can recognize a swordfish and put it to use, you’ll have enough techniques in your arsenal to solve the vast majority of very difficult newspaper puzzles. Certainly, you’ll be able to solve the puzzle we’re in the middle of right now, although I warn you—there is another Swordfish in your future. There’s a little more clearing to be done—consider hidden pairs. Then keep an eye out for 8s, with the loop starting from row one, column one.

Notice what happened there—by using a simpler technique, you help to set the situation for a more difficult one. That’s what solving is about—continually cycling through your technique arsenal. After you’ve cleared away some candidate clutter with a swordfish, you might want to search for hidden pairs or triplets (or even naked ones) to eliminate more pesky candidates. As you eliminate down to one value in some spaces, you may even go back to looking for naked singles as rows, columns, and boxes start filling up. It may take some fairly difficult tricks to get to the endgame, but you usually find yourself using the simplest techniques to finish a puzzle.

There are still higher levels of difficulty in sudoku than the hard newspaper puzzle. In these rarefied realms you might encounter the jellyfish, another closed logic loop—this time circling among eight points. Usually, you can find other, simpler ways to get candidates out of puzzle spaces. You may also have to push the puzzle’s logic (and your luck) to find devious solutions.

You might reach a point in a puzzle where you’ve cleared away enough candidates until you have a bunch of spaces with only two possibilities. Unfortunately, either value could be valid. By focusing on a space and choosing one of those possibilities, you take a “what if” stance and follow where logic leads you—pretty much like knocking over one domino to see how the rest fall. You’ll probably end up with an open-ended logic chain that yields a whole lot of possible answers. Then you go back to your starting point, choose the other possibility, and work out the resulting chain of logic from there. It may happen after a few spaces, or you may have to force a fairly long chain. What you’re looking for is a point where the two chains intersect—a space where, no matter what choice you make at the start, you find one value that is valid either way.

This gives you the starting point for a new chain of logic—after you’ve erased the chains of possibilities that led you there. This can be a pretty messy proposition, and it may be better to overlay the puzzle with tracing paper and make your deductions on that. You may want to differentiate your chains of logic by using different colors. Or you can mark candidates by using half circles. Start one chain by drawing a U-shaped half circle under your choices. Set off the next chain by drawing a half circle
above
your number choices. When your chain brings you to a space where you complete a circle, you’ll have found what you’re looking for.

With this technique, you’re not just building a chain but looking for weak links. Again, you’re operating in a situation where there are a number of two-choice, either-or spaces. You’ll make a choice and proceed on that assumption, looking to see whether the chain of logic you’re forcing crashes and burns. Perhaps it will lead you to a space where the only possible answer is already claimed in the row, column, or box. Or perhaps you’ll get an answer that eliminates all the candidates in a space.

Either way, you’ll know you’ve gone off on the wrong track. Nishio is not guessing—exactly. Like the forcing chains technique, it’s a way to assess the consequences of making a particular choice. Essentially, you’re looking for mistakes so that you can eliminate one of a given pair of choices.

The problem is, you can end up developing a fairly long chain before it crashes. There are even some cases where the chain never crashes, and you end up solving the puzzle!

Some people use Nishio as a form of quick check—“Can I get a certain number of valid moves from this choice, or does it quickly self-destruct?” If you decide to try Nishio, you’ll probably want to use some sort of overlay. Otherwise, by the time you finish erasing failed chains, your puzzle will look more like modern art than sudoku.