Read For the Love of Physics Online
Authors: Walter Lewin
Tags: #Biography & Autobiography, #Science & Technology, #Science, #General, #Physics, #Astrophysics, #Essays
For the Love of Physics (43 page)
Mammal Femurs
I
t’s reasonable to assume that the mass of a mammal is proportional to its volume. Let’s take a puppy and compare it with a full-grown dog that is four times bigger. I am assuming that all linear dimensions of the bigger dog are four times larger than that of the puppy—its height, its length, the length and the thickness of its legs, the width of its head, everything. If that is the case, then the volume (and thus the mass) of the bigger dog is about sixty-four times that of the puppy.
One way to see this is by taking a cube with sides
a, b
, and
c.
The volume of this cube is
a
×
b
×
c.
When you make all sides four times larger, the volume becomes 4
a
× 4
b
× 4
c
, which is 64
abc.
If we express this a bit more mathematically, we can say that the volume (thus the mass) of the mammal is proportional to its length to the third power. If the bigger dog is four times larger than the puppy, then its volume should be about 4 cubed (4
3
) times larger, which is 64. So, if we call the length of the femur “
l
,” then by comparing mammals of different size, their mass should be roughly proportional to
l
cubed (
l
3
).
Okay, that’s mass. Now, the strength of the mammal’s femur supporting all that weight has to be proportional to its thickness, right? Thicker bones can support more weight—that’s intuitive. If we translate that idea
to mathematics, the strength of the femur should be proportional to the area of the cross section of the bone. That cross section is roughly a circle, and we know that the area of a circle is π
r
2
, where
r
is the radius of the circle. Thus, the area is proportional to
d
2
if
d
is the diameter of the circle.
Let’s call the thickness of the femur “
d
” (for diameter). Then, following Galileo’s idea, the mass of the mammal would be proportional to
d
2
(so that the bones can carry the weight of the mammal), but it is also proportional to
l
3
(that is always the case, independent of Galileo’s idea). Thus, if Galileo’s idea is correct,
d
2
should be proportional to
l
3
, which is the same as stating that
d
is proportional to
l
3/2
.
If I compare two mammals and one is five times bigger than the other (thus the length
l
of its femur is about five times larger than that of the smaller mammal), I may expect that the thickness,
d
, of its femur is about 5
3/2
= 11 times greater than the thickness of the smaller animal’s femur. In lectures I showed that the length
l
of the femur of an elephant was about 100 times larger than the length of the femur of a mouse; we may therefore expect, if Galileo’s idea is correct, that the thickness,
d
, of the elephant’s femur is about 100
3/2
= 1,000 times thicker than that of the mouse.
Thus at some point, for very heavy mammals, the thickness of the bones would have to be the same as their lengths—or even greater—which would make for some pretty impractical mammals, and that would then be the reason why there is a maximum limit on the size of mammals.
APPENDIX 2

Newton’s Laws at Work
N
ewton’s law of universal gravitation can be written as

Here,
F
grav
is the force of gravitational attraction between an object of mass
m
1
and one of mass
m
2
, and
r
is the distance between them.
G
is called the gravitational constant.
Newton’s laws made it possible to calculate, at least in principle, the mass of the Sun and some planets.
Let’s see how this works. I’ll start with the Sun. Suppose
m
1
is the mass of the Sun, and that
m
2
is the mass of a planet (any planet). I will assume that the planetary orbit is a circle of radius
r
and let the orbital period of the planet be
T
(
T
is 365.25 days for the Earth, 88 days for Mercury, and almost twelve years for Jupiter).
If the orbit is circular or nearly so (which is the case for five of the six planets known in the seventeenth century), the speed of a planet in orbit is constant, but the direction of its velocity is always changing. However, whenever the direction of the velocity of any object changes, even if there is no change in speed, there must be an acceleration, and thus,
according to Newton’s second law, there must be a force to provide that acceleration.
It’s called the centripetal force (
F
c
), and it is always exactly in the direction from the moving planet toward the Sun. Of course, since Newton was Newton, he knew exactly how to calculate this force (I derive the equation in my lectures). The magnitude of this force is

Here
v
is the speed of the planet in orbit. But this speed is the circumference of the orbit, 2π
r
, divided by the time,
T
, it takes to make one revolution around the Sun. Thus we can also write:

Where does this force come from? What on earth (no pun implied) is the origin of this force? Newton realized that it must be the gravitational attraction by the Sun. Thus the two forces in the above equations are one and the same force; they are equal to each other:

If we massage this a bit further by rearranging the variables (this is your chance to brush up on your high school algebra), we find that the mass of the Sun is

Notice that the mass of the planet (
m
2
) is no longer present in equation 5; it does not enter into the picture; all we need is the planet’s mean distance to the Sun and its orbital period (
T
). Doesn’t that surprise you? After all,
m
2
shows up in equation 1 and also in equation 2. But the fact that it is present in both equations is the very reason that
m
2
is eliminated by setting
F
grav
equal to
F
c
. That’s the beauty of this method, and we owe all this to Sir Isaac!
Equation 5 indicates that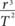 is the same for all planets. Even though they all have very different distances to the Sun and very different orbital
is the same for all planets. Even though they all have very different distances to the Sun and very different orbital
periods,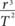 is the same for all. The German astronomer and mathematician Johannes Kepler had already discovered this amazing result in 1619, long before Newton. But why this ratio—between the cube of the radius and square of the orbital period—was constant was not understood at all. It was the genius Newton who showed sixty-eight years later that it is the natural consequence of his laws.
is the same for all. The German astronomer and mathematician Johannes Kepler had already discovered this amazing result in 1619, long before Newton. But why this ratio—between the cube of the radius and square of the orbital period—was constant was not understood at all. It was the genius Newton who showed sixty-eight years later that it is the natural consequence of his laws.
