Fortune's Formula (12 page)

B
OTH
S
MITH AND HIS SON,
Harold Junior, showed up at Thorp and Hand’s blackjack table. After getting the story from the dealer, there was some polite repartee. Smith Senior explained that there were individuals who took advantage of concentrations of cards that sometimes existed at the end of the deck. The telltale sign was someone raising the bet as the dealer neared the end of the deck.

A guy named Joe Bernstein had taken the Sahara Hotel in Las Vegas for $75,000 with an “ace count.” Word got out that Bernstein was headed for Harolds Club. Smith had warned his people to be on the lookout. He was not notified until Bernstein had $14,000 of Harolds’ money sitting in front of him. Bernstein would play seven hands at one table, leaving no room for anyone else. He saw every card. With eight hands in play (including the dealer’s), a deck was good for only two deals. On the first deal, Bernstein bet $5 a hand. He kept track of how many aces turned up. If he liked what he saw, he bet $500 a hand on the next deal.

Smith Senior instructed Thorp and Hand’s dealer to shuffle twelve to fifteen cards from the end of the deck. The two Smiths remained at the table to observe the results.

After Thorp won a few more hands, Senior told the dealer to shuffle twenty-five cards from the end.

Thorp won again, and Smith said to shuffle forty-two cards from the bottom. They would use only the top ten cards of the shuffled deck.

There was not much Thorp and Hand could do under those conditions. They left Harolds Club.

Thorp was curious to see the cheating dealer Kimmel had met. They went to the club where she worked, and Thorp bought $1,000 in chips. He made a bet of $30. The dealer had not finished dealing the hand when the pit boss halted her. He took the deck and handed it to a new dealer. She was the grim-faced woman with a touch of gray.

Thorp was dealt a pair of eights. The rules of blackjack allow players to split pairs. This means to turn a pair of same-value cards faceup and split them into two hands. The player receives a new, facedown card for each hand and plays them like regular hands. The player who splits must also double the original bet as he is playing two hands.

Thorp put down another $30 and split the eights. He drew cards and ended up with totals of 20 and 18, both strong hands.

The dealer had a three showing. She turned up her hole card. It was a ten. She had to hit her 13. Since Thorp and Hand knew what to look for, they saw what happened next. The dealer held the deck edge up and, with a finger, briefly bent back one corner of the deck’s top card. It was the queen of hearts. That would have busted her. With imperceptible sleight of hand, she dealt the second card to her hand. It was an eight. She had 21.

Eddie Hand bellowed out exactly what the dealer had done. Thorp joined in. The dealer showed no emotion save a blush. The pit boss listened to their story and said there was nothing he could do. It was their word against hers.

After each gambling session, Thorp met Kimmel and emptied his pockets onto the hotel bed. They counted the chips and cash to determine how well Thorp was doing. “He’d watch me like a hawk,” Thorp recalled. “One day I forgot to empty one pocket. I don’t know why; I was tired, caught up in the excitement of it all. He got this funny look on his face. ‘It looks like we’re short money.’ ‘
Oh
, I’ve got another bunch of chips.’ I’m sure that only enhanced his paranoia.”

Paranoia was in ample supply. The day after the experience with the cheating dealer, Thorp, Kimmel, and Hand drove to the small out-of-town casino. Thorp made a phone call. When he came back, Kimmel and Hand told him they had been barred from the casino. The floor manager said Thorp had won too consistently. They concluded that a system was involved.

Thorp returned to the Mapes. He played alone, betting $5 and up. The pit boss stepped over and told him he was no longer welcome. That went for his two friends—and any other friends he might have.

The next afternoon the three men drove to a casino at the south end of Lake Tahoe. Thorp bought $2,000 in chips and pushed his way to one of the few seats at a blackjack table. Two thousand dollars qualified him as a high roller at this place. A pit boss appeared and offered a free meal and show. Thorp asked if his two friends could be included in that invitation. The pit boss agreed. In a few minutes’ play, Thorp won $1,300 and Kimmel $2,000.

They ordered filet mignon and champagne for their comped dinner. This meal inspired such a spirit of gratitude that the men took their business to a neighboring casino.

This was Harvey’s Wagon Wheel. Thorp bought another $2,000 of chips. He managed to get a $25 minimum table and began winning. Kimmel joined him. According to plan, Thorp did the counting and signaled to Kimmel. It took thirty minutes to clean out the table’s money tray.

That is a rare event. The money is supposed to flow in the opposite direction. “Oh, help me, please help me,” the dealer pleaded.

The pit boss arrived with an entourage. As Thorp played, the pit boss attempted to account for his luck to the other personnel. The pit boss prescribed a new dealer. This did not stop Thorp and Kimmel’s winning streak. About two hours and five dealers later, they had emptied the money tray a second time. Thorp had won $6,000 and Kimmel $11,000.

Thorp told Kimmel it was time to quit. He was tired. As Thorp walked to cash in his chips, a beautiful young woman passed by. She smiled significantly. Then another, equally beautiful woman did the same thing.

Thorp did not have time to puzzle over his sudden popularity. Kimmel was still at the blackjack table. Kimmel told him he had a good reason for continuing to play.

The cards are hot, he said.

Thorp tried to pull him away. Kimmel clutched the table. “I…will…not…leave…this…place!” he announced.

Thorp sat down again. He continued counting and telegraphing the counts to Kimmel. As long as he was counting, Thorp resumed betting.

They began losing quickly. Thorp kept nagging Kimmel to quit. Forty-five minutes later he gave in. The two of them had lost $11,000.

As Eddie Hand had said, Kimmel was “more trouble than an $18 whore.”

This debacle still left them ahead about $13,000 for the trip. The next day, after losing another $2,000 downtown, Thorp was on another winning streak. This again commanded the attention of a casino owner. He gave the dealer instructions to shuffle whenever Thorp changed his bet size.

This is fatal to any viable card-counting system. Thorp tried to evade the owner’s remedy by playing more than one hand when the deck was hot. The dealer shuffled every time Thorp played more than one hand.

Thorp scratched his nose. The dealer shuffled. Thorp asked if the dealer was going to shuffle every time he scratched his nose.

Yes, the dealer said.

Thorp scratched his nose again. The dealer shuffled.

He asked if she intended to shuffle whenever he made any change whatsoever in his behavior.

Yes.

Thorp was playing with $20 chips. He asked for some $50 or $100 chips. The owner refused to sell him any. A new deck was brought out. It was displayed faceup and facedown. This is normally done to let the player verify that all the cards are present and the backs have not been marked. This time, it was the casino people who scrutinized the backs. The dealer said they believed that Thorp had such sharp vision that he was able to distinguish
unmarked
cards from their backs. He was memorizing printing defects. Or dirt.

Thorp stubbornly continued playing. The owner successively demanded that four brand-new decks be brought in about five minutes. The dealer now theorized that Thorp was memorizing the entire deck. He knew exactly which cards remained in the deck and bet accordingly.

Thorp said it was impossible for anyone to do that.

The dealer insisted that the pit boss could do that—he could memorize the whole deck. Thorp bet $5 that the pit boss
couldn’t
.

The pit boss and the dealer were silent.

How about $50? Thorp asked. Hand sweetened the offer to $500. The casino people would not accept. Thorp and Hand left.

They tried one more casino. When they asked for a private table, they were passed to another manager, who appeared to hail from the gay Mafia. He too said he knew what they were doing. They weren’t welcome.

This terminated the experiment. By Thorp’s estimation, they had built $10,000 into $21,000 in about 30 person-hours of play. (Had it not been for Kimmel’s ill-fated binge, they might have ended up with $32,000.)

They had some time to kill before leaving for the airport. Kimmel wanted to visit a friend who ran the Primadonna casino. He instructed Thorp
not
to use the system there. Thorp found three silver dollars in his pocket and played them anyway. The deck turned favorable, and Thorp accumulated $35 in about five minutes. Had it not been for Kimmel’s warning, he might have bet fifties rather than dollars.

M
ARTINGALE AND MANY OTHER
betting systems purport to work whether there is a house advantage or not. Not so the Kelly system. When the edge is zero or negative (as it almost always is in a casino) the Kelly system says not to bet at all.

You might say that this is the difference between fantasy and reality. The reality is that you can’t expect to make
any
money with an unfavorable wager. It would be nice if things were otherwise, but the world doesn’t work that way.

Given a favorable betting opportunity, the Kelly system promises maximum profit and protection against ruin. These goals may sound antithetical. It is worth looking at how the Kelly formula works in a casino situation.

The Kelly system avoids gambler’s ruin quite simply. It is a “proportional” betting system. This means that each wager is scaled to the current size of the bankroll. Since you bet only a prescribed fraction of what you’ve currently got, you can never run out of money. When you lose repeatedly, as will happen in any game of chance, bets scale down in proportion to your diminished wealth.

Casinos and racetracks have a minimum bet size. One potential problem with the Kelly system is having a losing streak erode your bankroll to a point where the Kelly bet is less than the minimum wager. In practice, this is rarely an issue. It just means that your initial stake has to be large compared to the minimum bet, so that the chance of this is negligible.

The exponential growth of wealth in the Kelly system is also a consequence of proportional betting. As the bankroll grows, you make larger bets. Assuming you have an edge, in the long run you will win more than you lose. Winnings will parlay.

Imagine making a series of even-money bets on the toss of a coin that you know to be biased, with a 55 percent chance of coming up heads. Naturally, you will bet on heads each time.

That itself does not guarantee a profit. Here’s a chart showing the results of four money management systems. All are betting on the exact same sequence of 500 tosses.

The simplest “system” of all is betting a fixed wager. Here the bet amount starts at 10 percent of the initial bankroll and does not vary thereafter. The line of the fixed-wager gambler’s wealth climbs slowly upward. However, this policy carries a chance of ruin. An unlucky streak could bust the fixed-stake bettor.

In the three other systems, the wager changes as the bankroll does. One extreme approach is to bet it all. You bet your entire bankroll on the first toss. If you win, you bet everything on the second toss. You keep parlaying as long as you can.

Four Money Management Systems

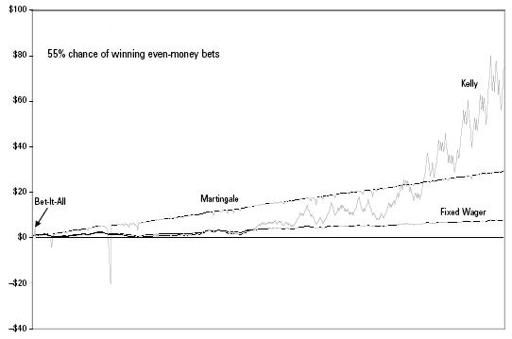
In 2004 a London man named Ashley Revell sold all his possessions, including his clothes, and staked his entire net worth of $135,300 on a roulette wheel at the Plaza Hotel in Las Vegas. Revell wore a rented tuxedo and bet on red. He won. He decided against going for double or nothing.

Revell was playing an unfavorable game. His actions would hardly have been less reckless had he had an edge. The bet-it-all policy works only until you lose.

In the chart above, the bet-it-all line begins with the small uptick at the far left. The first two tosses were heads, allowing the bet-it-all player to quadruple his money. He let it ride on the third toss, tails, and went bust. After that, the bet-it-all’s player’s wealth is zero.

At first glance, it may look like martingale does pretty well. The general slope of the martingale line beats the other systems for hundreds of bets. The wicked-looking downward spikes in the martingale line tell a different story. The spikes are streaks of bad luck. The martingale bettor is required to double his wager as long as he’s losing. This can lead to rapidly escalating losses.

These same unlucky streaks barely dented the other systems’ lines. For the martingale bettor, the bum luck is fatal. In this simulation, the martingale bettor goes bust on bet 19. The continuation of the line after that is irrelevant.

The line representing the Kelly system stands out in two ways. Notice that the general trend of the fixed-wager and martingale systems are straight lines, while the Kelly system is an upward curve. Notice also that the Kelly line is far more jittery than the other systems.

The wealth of the fixed-wager and martingale bettors tends to grow as an arithmetic series. The fixed-wager and martingale bettors are essentially earning a fixed hourly wage. They do not make bigger bets as their wealth grows. They are sitting on capital that could be put to use.

In comparison, the Kelly bettor’s wealth grows geometrically because he is making optimal use of capital. It takes a while for the Kelly strategy to get off the ground. In the left half of the chart, representing about 250 bets, the Kelly bettor’s line hugs that of the fixed-wager bettor. Much of the time, the fixed-wager bettor is ahead. Then the Kelly strategy takes off. The line swoops upward, leaving the other two systems far behind. In this particular simulation, the Kelly bettor has increased the original bankroll about 74-fold in 500 bets.

The Kelly system is not the only proportional betting system. There are an infinity of such betting systems. You could always bet 1 percent of your bankroll, or 10 percent, or 99 percent. You could bet
edge squared over the-last-number-that-came-up cubed
times your bankroll. What’s so special about the specific system that Kelly devised? The answer is simply that the Kelly system grows wealth faster than any other.

Below is a chart comparing the Kelly system to two other proportional betting systems. The chart tracks the same series of 500 biased coin tosses as above. The Kelly bettor runs $1 up into $74.46.

The line marked “underbet” is a proportional system where you bet exactly
half
the prescribed Kelly bet. The underbettor’s wealth grows much more steadily than the Kelly bettor’s. That is often a good thing. But the underbettor ends up with significantly less money ($16.07).

The line marked “overbet” is a system of betting twice the Kelly bet. This achieves $35.88 in this simulation. “Twice Kelly” is a treacherous system. It does well in lucky streaks, but all the gain is temporary. Notice that the overbettor was briefly the best-performing of the three systems early on (the little volcano-shaped peak at lower left). Then the overbettor’s wealth fell back to nearly zero and stayed there a long time afterward. Were the simulation continued indefinitely, the wealth of the twice-Kelly bettor would fall back to the original $1 or less an infinite number of times.

Underbetting vs. Overbetting

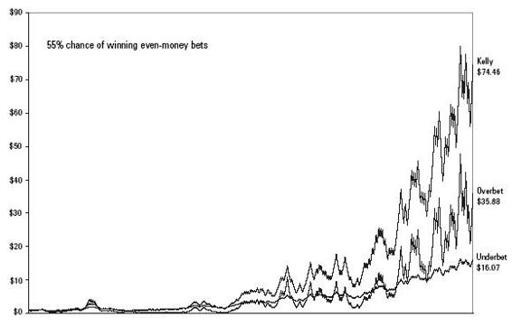
It could be worse. Overbetting can lead to virtual ruin, even with a proportional betting system. A line representing someone betting would be invisible on this chart, for it would hug the baseline. Such a bettor would run $1 down to $0.00000038 in 500 tosses. Were betting to continue, the bankroll would plunge endlessly downward, to ever-smaller millions of billionths of a cent.

Strictly speaking, the proportional overbettor will always have some microscopic fraction of a cent to his name (assuming that money is infinitely divisible and there are no minimum bets). This distinction is hardly worth bothering over.

The engine driving the Kelly system is the “law of large numbers.” In a 1713 treatise on probability, Swiss mathematician Jakob Bernoulli propounded a law that has been misunderstood by gamblers (and investors) ever since.

It concerns the tricky notion of expectation. In American roulette with a perfectly balanced wheel, a bet on red has an 18/38 chance of winning. Does that mean that red is guaranteed to come up 18 times out of every 38 times? No, of course not. (Who would be offering the “guarantee”?) Does it mean that if the wheel has been coming up black an awful lot lately, red is “due”? No (although many gamblers think so).

What does expectation mean then? Most who attempt to translate the math into plain English use the phrase “in the long run.” People say things like, “Red will come up 18/38 of the time,
in the long run
.”

This is only a figure of speech. No matter how many times you spin the wheel, there is never any certainty of achieving the expected number of reds.

Can you conclude that if you spin the wheel 38 trillion times, 18 trillion will be red? No. Will the number of reds be close to 18 trillion? It depends on what you mean by “close.” If you mean “Will it be between 17,999,999,999,995 and 18,000,000,000,005?” the answer is almost surely no. In fact, the difference between the actual and expected number of reds tends to
grow
with the number of spins.

Jakob Bernoulli’s law of large numbers says (only) that the
percentage
of reds will tend to approach the expected percentage as the number of spins increases. After trillions of spins, the percentage of reds will be very close to 18/38 or 47.37 percent.

Generations of innumerate gamblers have discovered this result to be of less practical value than they’d like. It is of no use in helping anyone profit from a negative-expectation bet.

You might well think that, provided you’re lucky enough to find a positive-expectation bet, the law of large numbers means you’ll do all right in the long run. Not necessarily! As we’ve seen, people can go bust in the short run. Even people using a proportional betting system can, for all intents and purposes, go broke.

Shannon invoked the law of large numbers throughout information theory. In a noisy communications channel where every bit is uncertain, the one certain thing is playing the percentages.

Kelly used an analogous approach to make money from positive-expectation bets. The Kelly system manages money so that the bettor stays in the game long enough for the law of large numbers to work.