Hidden Variables (18 page)

and this relation between R and z must hold
independent of the mass M.

An infinite number of (R,z) pairs will satisfy equation (4), and Table 1 lists some of them, together with the mass M, found from equation (3), and the distance, Z, where the gravitational acceleration towards the disc is one gee. Since we may as well use the most compact and lightest of the possible cases, we use the set: R = 50 meters, z = 0 meters, Z = 246.2 meters, GM = 62,500 square meters.

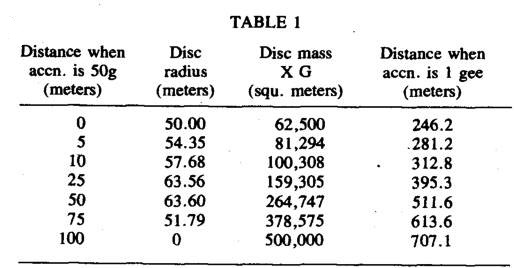
This means a mass plate 50 meters in radius, and projecting from it we have a column at least 246.2 meters long. The life capsule will ride up and down this as the drive acceleration is varied.

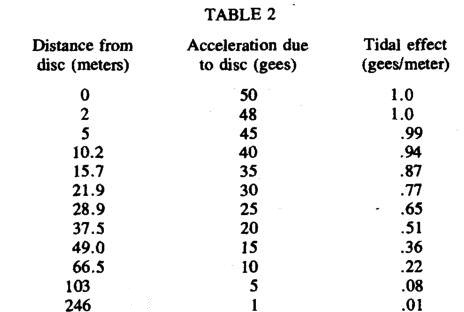
The only other thing that McAndrew needed to know was the gravitational acceleration and tidal effects at different distances from the plate. He would use these to decide how far away the life capsule should be positioned for different drive accelerations. Those values are provided from equations (2) and (3) and are shown in Table 2.

This story has worried a number of readers. They say, in summary, how can a ship that can only generate fifty gee of thrust ever escape from a field where it is just balancing a fifty gee attraction? It's a hypothetical question, since the beginning of the story points out that the fifty gee limit applies not to the
propulsion
system, but to the balancing system that neutralizes the propulsive acceleration. Even so, it's a nice question, and one easily answered.

If you are sitting balanced with a fifty gees thrust and a fifty gees attraction towards some central body, all you need do to escape is to turn the ship and direct the thrust
at right angles
to the direction of the attracting body. You then fall inwards at first, but the trajectory has a point of closest approach about 5,000 kilometers from the center of attraction—so we can only use this method for orbits about high-density and compact objects. If anyone is interested I can provide the actual trajectory and the profile of the escape spiral.

There is, however, still a problem with the story, and one less easily answered. It concerns the drive itself. McAndrew's ship generates its fifty gees acceleration by expelling reaction mass—necessary for any propulsion system that wishes to satisfy the law of conservation of linear momentum. Unless we wish to throw overboard the most basic laws of modern physics, reactionless drives are out, as are drives that somehow convert angular momentum to linear momentum. We are stuck with a drive that consumes reaction mass to achieve its propulsive effect.

Suppose that McAndrew's ship had a photon drive, in which matter is turned to radiation and the radiation, suitably directed, provides the thrust. That's the best we can imagine, if we accept today's physics. With a photon drive, it's easy to calculate that a sustained fifty gees drive will quickly consume the ship's own mass in order to keep on accelerating. Half the mass would be gone in a few days, and McAndrew's ship would disappear from under him.

There is one loophole, a solution based on a known inconsistency between general relativity and quantum theory. To explore that loophole, see "All The Colors of the Vacuum," later in this collection.

THE NEW PHYSICS: THE SPEED OF LIGHTNESS, CURVED SPACE, AND OTHER HERESIES

Listwolme is a small world with a thin but permanently cloudy atmosphere. The inhabitants have never seen the stars, nor become aware of anything beyond their own planet. There is one main center of civilization which confined itself to a small region of the surface until about a hundred years ago, when an industrial revolution took place. For the first time, rapid transportation over substantial areas of the planet became possible.

Orbital velocity at the surface of Listwolme is less than two kilometers a second. The meetings of the Listwolme Scientific Academy following the development of high-velocity surface vehicles are chronicled below. The highlights of those meetings were undoubtedly the famous exchanges between Professor Nessitor and Professor Spottipon.

* * *

The first debate: In which Professor Nessitor reveals the curious results of his experiments with high-speed vehicles, and proposes a daring hypothesis.

Nessitor:
As Members of the Academy will recall, a few months ago I began to install sensitive measuring devices aboard the
Tristee Two,
the first vehicle to move at a speed more than ten times that of a running
schmitzpoof.
The work was not easy, because it was first necessary to suppress all vibration induced by the car's contact with the surface.

One month ago we achieved the right combination of smooth suspension and vibration damping. It was with some excitement that I placed one of our instruments, a sensitive spring balance, within the vehicle and we began steadily to increase our speed. As you may have heard, there have been reports of "feeling light" from the drivers of these cars when they go at maximum velocity.

Fellow scientists, those feelings are no illusion! Our instruments showed a definite decrease in load on the balance as our speed was increased. There is a relationship between
weight
and
motion!

(As Nessitor paused, there was a murmur of surprise and incredulity around the great hall. Professor Spottipon rose to his feet.)

Spottipon:
Professor Nessitor, your reputation is beyond question . What would arouse scepticism from another in your case is treated with great respect. But your statement is so amazing that we would like to hear more of these experiments. For example, I have heard of this "lightening" effect at high speeds, but seen no quantitative results. Were your balances sensitive enough to measure some relation between the lightness and the speed?

Nessitor
(triumphantly): With great precision. We measured the weight shown on the balance at a wide variety of speeds, and from this I have been able to deduce a precise formula between the measured weight, the original weight when the vehicles was at rest, and the speed of movement. It is as follows.

(Here Professor Nessitor went to the central display screen and sketched on it the controversial formula. It is believed that this was the first time it had ever appeared to public view. In the form that Nessitor used, it reads: (Weight at speed v) = (Rest weight) X (1 - v
²
/c
²
) When the formula was exhibited there was a silence, while the others examined its implications.)

Spottipon
(thoughtfully): I think I can follow the significance of most of this. But what is the constant, c, that appears in your equation?

Nessitor:
It is a velocity, a new constant of nature. Since it measures the degree to which an object is lightened when it moves with velocity v, I suggest that the basic constant, c, should be termed the "speed of lightness".

Spottipon
(incredulously): You assert that this holds anywhere on Listwolme? That your formula does not depend on the
position
where the experiment is conducted?
Nessitor:
That is indeed my contention. In a series of experiments at many places on the surface, the same result was obtained everywhere, with the same velocity, "c". It is almost four times as fast as our fastest car.

(There was a long pause, during which Professor Spottipon was seen to be scribbling rapidly on a scribe pad. When he had finished his face bore a look of profound inspiration.)

Spottipon:
Professor Nessitor, the formula you have written has some strange implications. You assert that there is a lightening of weight with speed across the surface. This we might accept, but you have not taken your formula to its logical limit. Do you realize that there must be a speed when the weight
vanishes?
When v = c, you have a situation where an object does not push at all on the balance! Worse than that, if v
exceeds
your "speed of lightness" you would calculate a
negative
weight. If that were true, a car moving at such a speed would fly completely off the surface. You would have created the long-discussed and arguably impossible "flying machine."

Nessitor
(calmly): As Professor Spottipon has observed with his usual profound insight, the speed of lightness is a most fundamental constant. My interpretation is as follows: since it is clearly ridiculous that an object should have negative weight, the formula is trying to tell us something very deep. It is pointing out that
there is no way that an object can ever exceed the speed of lightness.
The speed that we can deduce from these experiments, c, represents the ultimate limit of speed that can ever be attained.

(Sensation. The assembled scientists began to talk among themselves, some frankly disbelieving, others pulling forth their scribe pads and writing their own calculations. At last a loud voice was heard above the general hubbub.)

Voice:
Professor Nessitor! Do you have any name for this new theory of yours?

Nessitor
(shouting to be heard): I do. Since the effects depend only on the motion
relative
to the ground, I suggest the new results should be termed the PRINCIPLE OF RELATIVITY. I think that . . .

(Professor Nessitor's next comments were unfortunately lost in the general noise of the excited assembly.)

* * *

Six months passed before Professor Nessitor appeared again at a meeting of the Academy. In those months, there had been much speculation and heated argument, with calls for more experiments. It was to an expectant but still sceptical audience that the Professor made his second address.

Nessitor:
Distinguished colleagues, last time that I was here there were calls for proof, for some fundamental basis for the formula I presented to you then. It was to answer those calls that I embarked, four months ago, on a new set of experiments with the
Tristee Two
vehicle. We had installed a new instrument on board our car. It measures distances very accurately, and permits the car's course to be controlled to an absolutely straight line. For it had occurred to me to ask the question, if velocity and weight are so closely linked, could it be that
distance
itself depends on some unknown factors?

Spottipon
(somewhat irritably): With all due respect, Nessitor, I have no idea what you mean by such a statement. Distance is distance, no matter how fast you traverse it. What could you hope to find? I hoped that you would have repeated the experiments on speed and weight.

Nessitor:
My esteemed colleague, please have patience. Permit me to tell you what happened. We set the
Tristee Two
to travel a long distance at various speeds. And indeed, we confirmed the speed-weight relation. At the same time, we were measuring the distance travelled. But in performing this experiment we were moving longer linear distances over the surface of Listwolme than any other scientific group had ever done.

I therefore decided to conduct an experiment. We travelled a long distance in a certain direction, accurately measuring this with our new instrument. Then we made a half turn and proceeded far along this new line, again measuring distance all the way. Finally, we headed straight back to our original starting point, following the hypotenuse of the triangle and measuring this distance also.

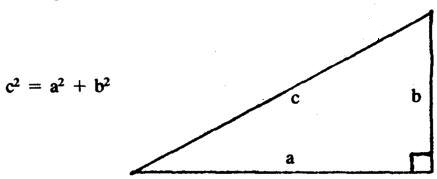
Now, we are all familiar with the Sharog-Paty Theorem that relates the lengths of the sides of a right-angled triangle.

(Nessitor went to the central display panel and scribed the famous Sharog-Paty relation: