Hyperspace (13 page)

His son Charles, however, seemed doomed to lead a respectable, boring life as a mathematician. He was fascinated not by polygamy, but by polygons! Having graduated from Oxford in 1877, he became a respectable master at the Uppingham School while working on his master’s
degree in mathematics. At Oxford, Hinton became intrigued with trying to visualize the fourth dimension. As a mathematician, he knew that one cannot visualize a four-dimensional object in its entirety. However, it is possible, he reasoned, to visualize the cross section or the unraveling of a four-dimensional object.

Hinton published his notions in the popular press. He wrote the influential article “What is the Fourth Dimension?” for the
Dublin University Magazine
and the
Cheltenham Ladies’ College Magazine
, reprinted in 1884 with the catchy subtitle “Ghosts Explained.”

Hinton’s life as a comfortable academic, however, took a sharp turn for the worse in 1885 when he was arrested for bigamy and put on trial. Earlier, Hinton had married Mary Everest Boole, the daughter of a member of his father’s circle, and widow of the great mathematician George Boole (founder of Boolean algebra). However, he was also the father of twins born to a certain Maude Weldon.

The headmaster at Uppingham, noticing Hinton in the presence of his wife, Mary, and his mistress, Maude, had assumed that Maude was Hinton’s sister. All was going well for Hinton, until he made the mistake of marrying Maude as well. When the headmaster learned that Hinton was a bigamist, it set off a scandal. He was promptly fired from his job at Uppingham and placed on trial for bigamy. He was imprisoned for 3 days, but Mary Hinton declined to press charges and together they left England for the United States.

Hinton was hired as an instructor in the mathematics department at Princeton University, where his obsession with the fourth dimension was temporarily sidetracked when he invented the baseball machine. The Princeton baseball team benefited from Hinton’s machine, which could fire baseballs at 70 miles per hour. The descendants of Hinton’s creation can now be found on every major baseball field in the world.

Hinton was eventually fired from Princeton, but managed to get a job at the United States Naval Observatory through the influence of its director, a devout advocate of the fourth dimension. Then, in 1902, he took a job at the Patent Office in Washington.

Hinton spent years developing ingenious methods by which the average person and a growing legion of followers, not only professional mathematicians, could “see” four-dimensional objects. Eventually, he perfected special cubes that, if one tried hard enough, could allow one to
visualize hypercubes, or cubes in four dimensions. These would eventually be called Hinton’s cubes. Hinton even coined the official name for an unraveled hypercube, a tesseract, which found its way into the English language.

Hinton’s cubes were widely advertised in women’s magazines and were even used in seances, where they soon became objects of mystical importance. By mediating on Hinton’s cubes, it was claimed by members of high society, you could catch glimpses of the fourth dimension and hence the nether world of ghosts and the dearly departed. His disciples spent hours contemplating and meditating on these cubes, until they attained the ability to mentally rearrange and reassemble these cubes via the fourth dimension into a hypercube. Those who could perform this mental feat, it was said, would attain the highest state of nirvana.

As an analogy, take a three-dimensional cube. Although a Flatlander cannot visualize a cube in its entirety, it is possible for us to unravel the cube in three dimensions, so that we have a series of six squares making a cross. Of course, a Flatlander cannot reassemble the squares to make a cube. In the second dimension, the joints between each square are rigid and cannot be moved. However, these joints are easy to bend in the third dimension. A Flatlander witnessing this event would see the squares disappear, leaving only one square in his universe (
Figure 3.6
).

Likewise, a hypercube in four dimensions cannot be visualized. But one can unravel a hypercube into its lower components, which are ordinary three-dimensional cubes. These cubes, in turn, can be arranged in a three-dimensional cross—a tesseract. It is impossible for us to visualize how to wrap up these cubes to form a hypercube. However, a higher-dimensional person can “lift” each cube off our universe and then wrap up the cube to form a hypercube. (Our three-dimensional eyes, witnessing this spectacular event, would only see the other cubes disappear, leaving only one cube in our universe.) So pervasive was Hinton’s influence that Salvadore Dali used Hinton’s tesseract in his famous painting
Christus Hypercubus
, on display at the Metropolitan Museum of Art in New York, which depicts Christ being crucified on a four-dimensional cross (
Figure 3.7
).

Hinton also knew of a second way to visualize higher-dimensional objects: by looking at the shadows they cast in lower dimensions. For example, a Flatlander can visualize a cube by looking at its two-dimensional shadow. A cube looks like two squares joined together. Similarly, a hypercube’s shadow cast on the third dimension becomes a cube within a cube (
Figure 3.8
).

In addition to visualizing unravelings of hypercubes and examining their shadows, Hinton was aware of a third way to conceptualize the fourth dimension: by cross sections. For example, when Mr. Square is sent into the third dimension, his eyes can see only two-dimensional cross sections of the third dimension. Thus he can see only circles appear, get larger, change color, and then suddenly disappear. If Mr. Square moved past an apple, he would see a red circle materialize out of nowhere, gradually expand, then contract, then turn into a small brown circle (the stem), and finally disappear. Likewise, Hinton knew that if we were hurled into the fourth dimension, we would see strange objects suddenly appear out of nowhere, get larger, change color, change shape, get smaller, and finally disappear.

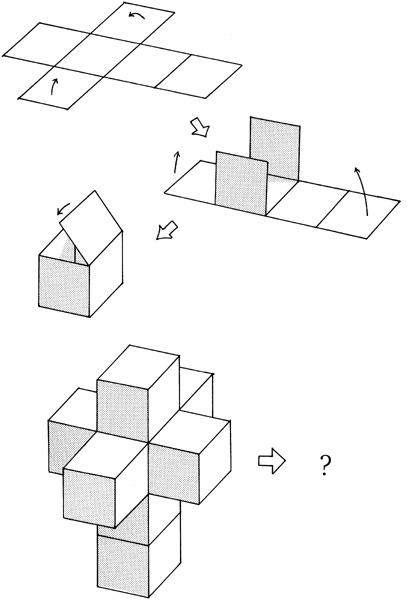
Figure 3.6. Flatlanders cannot visualize a cube, but they can conceptualize a three-dimensional cube by unraveling it. To a Flatlander, a cube, when unfolded, resembles a cross, consisting of six squares. Similarly, we cannot visualize a four-dimensional hypercube, but if we unfold it we have a series of cubes arranged in a crosslike tesseract. Although the cubes of a tesseract appear immobile, a four-dimensional person can “wrap up” the cubes into a hypercube
.

Figure 3.7. In
Christus Hypercubus,
Salvadore Dali depicted Christ as being crucified on a tesseract, an unraveled hypercube. (The Metropolitan Museum of Art. Gift of Chester Dale, Collection, 1955. © 1993. Ars, New York/Demart Pro Arte, Geneva)

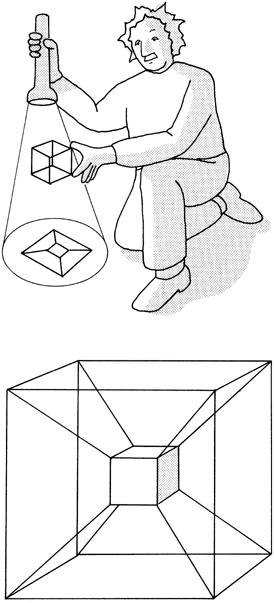
Figure 3.8. A Flatlander can visualize a cube by examining its shadow, which appears as a square within a square. If the cube is rotated, the squares execute motions that appear impossible to a Flatlander. Similarly, the shadow of a hypercube is a cube within a cube. If the hypercube is rotated in four dimensions, the cubes execute motions that appear impossible to our three-dimensional brains
.

In summary, Hinton’s contribution may be his popularization of higher-dimensional figures using three methods: by examining their shadows, their cross sections, and their unravellings. Even today, these three methods are the chief ways in which professional mathematicians and physicists conceptualize higher-dimensional objects in their work. The scientists whose diagrams appear in today’s physics journals owe a small debt of gratitude to Hinton’s work.

In his articles, Hinton had answers for all possible questions. When people asked him to name the fourth dimension, he would reply that the words
ana
and
kata
described moving in the fourth dimension and were the counterparts of the terms
up
and
down
, or
left
and
right
. When asked where the fourth dimension was, he also had a ready answer.

For the moment, consider the motion of cigarette smoke in a closed room. Because the atoms of the smoke, by the laws of thermodynamics, spread and diffuse into all possible locations in the room, we can determine if there are any regions of ordinary three-dimensional space that the smoke molecules miss. However, experimental observations show that there are no such hidden regions. Therefore, the fourth spatial dimension is possible only if it is smaller than the smoke particles. Thus if the fourth dimension actually exists, it must be incredibly small, even smaller than an atom. This is the philosophy that Hinton adopted, that all objects in our three-dimensional universe exist in the fourth dimension, but that the fourth dimension is so small that it evades any experimental observation. (We will find that physicists today adopt essentially the same philosophy as Hinton and conclude that the higher dimensions are too small to be experimentally seen. When asked, “What is light?” he also had a ready answer. Following Riemann, Hinton believed that
light is a vibration of the unseen fourth dimension, which is essentially the viewpoint taken today by many theoretical physicists.)

In the United States, Hinton single-handedly sparked an enormous public interest in the fourth dimension. Popular magazines like
Harper’s Weekly, McClure’s, Current Literature, Popular Science Monthly
, and
Science
all devoted pages to the blossoming interest in the fourth dimension. But what probably ensured Hinton’s fame in America was the famous contest sponsored by
Scientific American
in 1909. This unusual contest offered a $500 prize (a considerable amount of money in 1909) to “the best popular explanation of the Fourth Dimension.” The magazine’s editors were pleasantly surprised by the deluge of letters that poured into their offices, including entries from as far away as Turkey, Austria, Holland, India, Australia, France, and Germany.

The object of the contest was to “set forth in an essay not longer than twenty-five hundred words the meaning of the term so that the ordinary lay reader could understand it.” It drew a large number of serious essays. Some lamented the fact that people like Zollner and Slade had besmirched the reputation of the fourth dimension by confusing it with spiritualism. However, many of the essays recognized Hinton’s pioneering work on the fourth dimension. (Surprisingly, not one essay mentioned the work of Einstein. In 1909, it was still far from clear that Einstein had uncovered the secret of space and time. In fact, the idea of time as the fourth dimension did not appear in a single essay.)

Without experimental verification, the
Scientific American
contest could not, of course, resolve the question of the existence of higher dimensions. However, the contest did address the question of what higher-dimensional objects might look like.

What would it be like to meet a creature from a higher dimension?

Perhaps the best way to explain the wonder and excitement of a hypothetical visit to other dimensions is through science fiction, where writers have tried to grapple with this question.