Hyperspace (35 page)

Think of the video screen as a sheet of paper. Since points at the top of the screen are identical to the points at the bottom, we can seal the top and bottom sides together with glue. We now have rolled the sheet of paper into a tube. But the points on the left side of the tube are identical to the points on the right side of the tube. One way to glue these two ends is to bend the tube carefully into a circle, and seal the two open ends together with glue (
Figure 9.2
).

What we have done is to turn a sheet of paper into a doughnut. A rocket ship wandering on the video screen can be described as moving on the surface of an inner tube. Every time the rocket vanishes off the
video screen and reappears on the other side of the screen, this corresponds to the rocket ship moving across the glued joint of the inner tube.

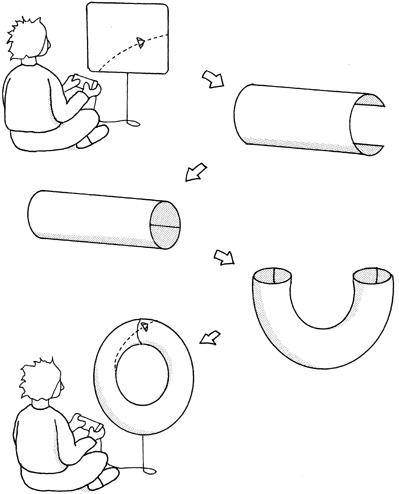
Figure 9.2. If a rocket disappears off the right side of a video-game screen, it re-emerges on the left. If it disappears at the top, it re-emerges at the bottom. Let us now wrap the screen so that identical points match. We first match the top and bottom points by wrapping up the screen. Then we match the points on the left-and right-hand sides by rolling up the screen like a tube. In this way, we can show that a video-game screen has the topology of a doughnut
.

Vafa conjectures that our sister universe has the shape of some sort of twisted six-dimensional torus. Vafa and his colleagues have pioneered the concept that our sister universe can be described by what mathematicians call an
orbifold
. In fact, his proposal that our sister universe has the topology of an orbifold seems to fit the observed data rather well.
³

To visualize an orbifold, think of moving 360 degrees in a circle. Everyone knows that we come back to the same point. In other words, if I dance 360 degrees around a May pole, I know that I will come back to the same spot. In an orbifold, however, if we move less than 360 degrees around the May pole, we will still come back to the same point. Although this may sound preposterous, it is easy to construct orbifolds. Think of Flatlanders living on a cone. If they move less than 360 degrees around the apex of the cone, they arrive at the same spot. Thus an orbifold is a higher-dimensional generalization of a cone (
Figure 9.3
).

To get a feel for orbifolds, imagine that some Flatlanders live on what is called a Z-orbifold, which is equivalent to the surface of a square bean bag (like those found at carnivals and country fairs). At first, nothing seems different from living in Flatland itself. As they explore the surface, however, they begin to find strange happenings. For example, if a Flatlander walks in any direction long enough, he returns to his original position as though he walked in a circle. However, Flatlanders also notice that there is something strange about certain points in their universe (the four points of the bean bag). When walking around any of these four points by 180 degrees (not 360 degrees), they return to the same place from which they started.

The remarkable thing about Vafa’s orbifolds is that, with just a few assumptions, we can derive many of the features of quarks and other subatomic particles. (This is because, as we saw earlier, the geometry of space in Kaluza-Klein theory forces the quarks to assume the symmetry of that space.) This gives us confidence that we are on the right track. If these orbifolds gave us totally meaningless results, then our intuition would tell us that there is something fundamentally wrong with this construction.

If none of the solutions of string theory contains the Standard Model, then we must throw away superstring theory as another promising but ultimately incorrect theory. However, physicists are excited by the fact that it is possible to obtain solutions that are tantalizingly close to the Standard Model.

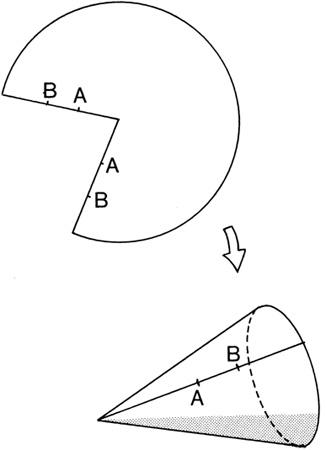
Figure 9.3. If we join points A and B, then we form a cone, which is the simplest example of an orbifold. In string theory, our four-dimensional universe may have a six-dimensional twin, which has the topology of an orbifold. However, the six-dimensional universe is so small that it is unobservable
.

Mathematicians for the past 80 years have been working out the properties of these weird surfaces in higher dimensions, ever since the French mathematician Henri Poincaré pioneered the subject of topology in the early twentieth century. Thus the ten-dimensional theory is able to incorporate a large body of modern mathematics that previously seemed quite useless.

In particular, the rich storehouse of mathematical theorems compiled by mathematicians over the past century are now being used to explain why there are three families of particles. As we saw earlier, one disastrous feature of the GUTs is that there are three identical families of quarks and leptons. However, orbifolds may explain this disconcerting feature of the GUTs.
⁴

Vafa and his co-workers have discovered many promising solutions to the string equations that appear to resemble the physical world. With a remarkably small set of assumptions, in fact, they can rederive the Standard Model, which is an important step for the theory. This is, in fact, both the strength and the weakness of superstring theory. Vafa and his co-workers have been, in a way, too successful: They have found millions of other possible solutions to the string equations.

The fundamental problem facing superstring theory is this:
Of the millions of possible universes that can be mathematically generated by superstring theory, which is the correct one?
As David Gross has said,

[T]here are millions and millions of solutions that have three spatial dimensions. There is an enormous abundance of possible classical solutions.… This abundance of riches was originally very pleasing because it provided evidence that a theory like the heterotic string could look very much like the real world. These solutions, in addition to having four space-time dimensions, had many other properties that resemble our world—the right kinds of particles such as quarks and leptons, and the right kinds of interactions.… That was a source of excitement two years ago.
⁵

Gross cautions that although some of these solutions are very close to the Standard Model, other solutions produce undesirable physical properties: “It is, however, slightly embarrassing that we have so many solutions but no good way of choosing among them. It seems even more embarrassing that these solutions have, in addition to many desired properties, a few potentially disastrous properties.”
⁶
A layperson, hearing
this for the first time, may be puzzled and ask: Why don’t you just calculate which solution the string prefers? Since string theory is a well-defined theory, it seems puzzling that physicists cannot calculate the answer.

The problem is that the perturbation theory, one of the main tools in physics, is of no use. Perturbation theory (which adds up increasingly small quantum corrections) fails to break the ten-dimensional theory down to four and six dimensions. Thus we are forced to use nonperturbative methods, which are notoriously difficult to use. This, then, is the reason why we cannot solve string theory. As we said earlier, string field theory, developed by Kikkawa and me and further improved by Witten, cannot at present be solved nonperturbatively. No one is smart enough.

I once had a roommate who was a graduate student in history. I remember one day he warned me about the computer revolution, which eventually might put physicists out of a job. “After all,” he said, “computers can calculate everything, can’t they?” To him, it was only a matter of time before mathematicians put all physics questions in the computer and physicists got on the unemployment line.

I was taken aback by the comment, because to a physicist a computer is nothing more than a sophisticated adding machine, an impeccable idiot. It makes up in speed what it lacks in intelligence. You have to input the theory into the computer before it can make a calculation. The computer cannot generate new theories by itself.

Furthermore, even if a theory is known, the computer may take an infinite amount of time to solve a problem. In fact, computing all the really interesting questions in physics would take an infinite amount of computer time. This is the problem with string theory. Although Vafa and his colleagues have produced millions of possible solutions, it would take an infinite amount of time to decide which of the millions of possibilities was the correct one, or to calculate solutions to quantum problems involving the bizarre process of tunneling, one of the most difficult of quantum phenomena to solve.

In the final analysis, we are asking the same question posed by Kaluza in 1919—Where did the fifth dimension go?—except on a much higher level. As Klein pointed out in 1926, the answer to this question has to do with quantum theory. Perhaps the most startling (and complex) phenomenon in quantum theory is tunneling.

For example, I am now sitting in a chair. The thought of my body suddenly zapping through the molecules of the wall next to me and reassembling, uninvited, in someone else’s living room is an unpleasant one. Also an unlikely one. However, quantum mechanics postulates that there is a finite (although small) probability that even the most unlikely, bizarre events—such as waking up one morning and finding our bed in the middle of the Amazon jungle—will actually happen. All events, no matter how strange, are reduced by quantum theory to probabilities.

This tunneling process sounds more like science fiction than real science. However, tunneling can be measured in the laboratory and, in fact, solves the riddle of radioactive decay. Normally, the nucleus of an atom is stable. The protons and neutrons within the nucleus are bound together by the nuclear force. However, there is a small probability that the nucleus might fall apart, that the protons and neutrons might escape by tunneling past the large energy barrier, the nuclear force, that binds the nucleus together. Ordinarily, we would say that all nuclei must therefore be stable. But it is an undeniable fact that uranium nuclei do, in fact, decay when they shouldn’t; in fact, the conservation of energy law is briefly violated as the neutrons in the nucleus tunnel their way through the barrier.

The catch, however, is that these probabilities are vanishingly small for large objects, such as humans. The probability of our tunneling through a wall within the lifetime of the known universe is infinitesimally small. Thus I can safely assume that I will not be ungraciously transported through the wall, at least within my own lifetime. Similarly, our universe, which originally might have begun as a ten-dimensional universe, was not stable; it tunneled and exploded into a four- and a six-dimensional universe.

To understand this form of tunneling, think of an imaginary Charlie Chaplin film, in which Chaplin is trying to stretch a bed sheet around an oversize bed. The sheet is the kind with elastic bands on the corners. But it is too small, so he has to strain to wrap the elastic bands around each corner of the mattress, one at a time. He grins with satisfaction once he has stretched the bed sheet smoothly around all four corners of the bed. But the strain is too great; one elastic band pops off one corner, and the bed sheet curls up. Frustrated, he pulls this elastic around the corner, only to have another elastic pop off another corner. Every time he yanks an elastic band around one corner, another elastic pops off another corner.

This process is called
symmetry breaking
. The smoothly stretched bed sheet possesses a high degree of symmetry. You can rotate the bed 180
degrees along any axis, and the bed sheet remains the same. This highly symmetrical state is called the
false vacuum
. Although the false vacuum appears quite symmetrical, it is not stable. The sheet does not want to be in this stretched condition. There is too much tension. The energy is too high. Thus one elastic pops off, and the bed sheet curls up. The symmetry is broken, and the bed sheet has gone to a lower-energy state with less symmetry. By rotating the curled-up bed sheet 180 degrees around an axis, we no longer return to the same sheet.