Hyperspace (40 page)

Reeling from these disasters, rejected by society, scorned by fate, “he” becomes a drunkard and drifter. Not only has Jane lost her parents and her lover, but he has lost his only child as well. Years later, in 1970, he stumbles into a lonely bar, called Pop’s Place, and spills out his pathetic story to an elderly bartender. The sympathetic bartender offers the drifter the chance to avenge the stranger who left her pregnant and
abandoned, on the condition that he join the “time travelers corps.” Both of them enter a time machine, and the bartender drops off the drifter in 1963. The drifter is strangely attracted to a young orphan woman, who subsequently becomes pregnant.

The bartender then goes forward 9 months, kidnaps the baby girl from the hospital, and drops off the baby in an orphanage back in 1945. Then the bartender drops off the thoroughly confused drifter in 1985, to enlist in the time travelers corps. The drifter eventually gets his life together, becomes a respected and elderly member of the time travelers corps, and then disguises himself as a bartender and has his most difficult mission: a date with destiny, meeting a certain drifter at Pop’s Place in 1970.

The question is: Who is Jane’s mother, father, grandfather, grandmother, son, daughter, granddaughter, and grandson? The girl, the drifter, and the bartender, of course, are all the same person. These paradoxes can made your head spin, especially if you try to untangle Jane’s twisted parentage. If we draw Jane’s family tree, we find that all the branches are curled inward back on themselves, as in a circle. We come to the astonishing conclusion that she is her own mother and father! She is an entire family tree unto herself.

Relativity gives us a simple method to sort through the thorniest of these paradoxes. We will make use of the “world line” method, pioneered by Einstein.

For example, say our alarm clock wakes us up one day at 8:00
A.M.,
and we decide to spend the morning in bed instead of going to work. Although it appears that we are doing nothing by loafing in bed, we are actually tracing out a “world line.”

Take a sheet of graph paper, and on the horizontal scale put “distance” and on the vertical scale put “time.” If we simply lie in bed from 8:00 to 12:00, our world line is a straight vertical line. We went 4 hours into the future, but traveled no distance. Even engaging in our favorite pastime, doing nothing, creates a world line. (If someone ever criticizes us for loafing, we can truthfully claim that, according to Einstein’s theory of relativity, we are tracing out a world line in four-dimensional space-time.)

Now let’s say that we finally get out of bed at noon and arrive at work at 1:00
P.M.
Our world line becomes slanted because we are moving in
space as well as time. In the lower left corner is our home, and on the upper right is our office (
Figure 11.1
). If we take the car to work, though, we arrive at the office earlier, at 12:30. This means that the faster we travel, the more our world line deviates from the vertical. (Notice that there is also a “forbidden region” in the diagram that our world line can’t enter because we would have to be going faster than the speed of light.)

One conclusion is immediate. Our world line never really begins or ends. Even when we die, the world lines of the molecules in our bodies keep going. These molecules may disperse into the air or soil, but they will trace out their own never-ending world lines. Similarly, when we are born, the world lines of the molecules coming from our mother coalesce into a baby. At no point do world lines break off or appear from nothing.

To see how this all fits together, take the simple example of our own personal world line. In 1950, say, our mother and father met, fell in love, and produced a baby (us). Thus the world lines of our mother and father collided and produced a third world line (ours). Eventually, when someone dies, the world lines forming the person disperse into billions of world lines of our molecules. From this point of view, a human being can be defined as a temporary collection of world lines of molecules. These world lines were scattered before we were born, came together to form our bodies, and will rescatter after we die. The Bible says, “from dust to dust.” In this relativistic picture, we might say, “from world lines to world lines.”

Our world line thus contains the entire body of information concerning our history. Everything that ever happened to us—from our first bicycle, to our first date, to our first job—is recorded in our world line. In fact, the great Russian cosmologist George Gamow, who was famous for approaching Einstein’s work with wit and whimsy, aptly titled his autobiography
My World Line
.

With the aid of the world line, we can now picture what happens when we go back in time. Let’s say we enter a time machine and meet our mother before we are born. Unfortunately, she falls in love with us and jilts our father. Do we really disappear, as depicted in
Back to the Future?
On a world line, we now see why this is impossible. When we disappear, our world line disappears. However, according to Einstein, world lines cannot be cut. Thus altering the past is not possible in relativity.

The second paradox, involving re-creating the past, poses interesting problems, however. For example, by going back in time, we are fulfilling the past, not destroying it. Thus the world line of the inventor of time
travel is a closed loop. His world line
fulfills
, rather than changes, the past.

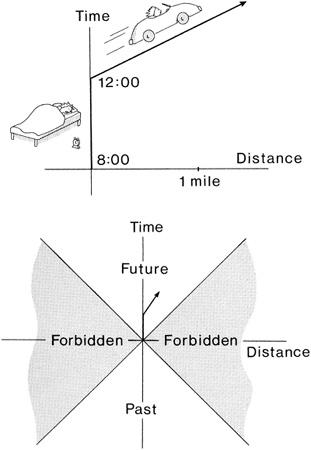
Figure 11.1. Our world line summarizes our entire history, from birth to death. For example, if we lie in bed from 8:00
A.M
. to 12:00, our world line is a vertical line. If we travel by car to work, then our world becomes a slanted line. The faster we move, the more slanted our world line becomes. The fastest we can travel, however, is the speed of light. Thus part of this space-time diagram is
“
forbidden
”;
that is, we would have to go faster than the speed of light to enter into this forbidden zone
.

Much more complicated is the world line of “Jane,” the woman who is her own mother and father and son and daughter (
Figure 11.2
).

Notice, once again, that we cannot alter the past. When our world line goes back in time, it simply fulfills what is already known. In such a universe, therefore, it is possible to meet yourself in the past. If we live through one cycle, then sooner or later we meet a young man or woman who happens to be ourselves when we were younger. We tell this young person that he or she looks suspiciously familiar. Then, thinking a bit, we remember that when we were young, we met a curious, older person who claimed that we looked familiar.

Thus perhaps we can fulfill the past, but never alter it. World lines, as we have stressed, cannot be cut and cannot end. They can perhaps perform loops in time, but never alter it.

These light cone diagrams, however, have been presented only in the framework of special relativity, which can describe what happens if we enter the past, but is too primitive to settle the question of whether time travel makes any sense. To answer this larger question, we must turn to the general theory of relativity, where the situation becomes much more delicate.

With the full power of general relativity, we see that these twisted world lines might be physically allowed. These closed loops go by the scientific name
closed timelike curves
(CTCs). The debate in scientific circles is whether CTCs are allowed by general relativity and quantum theory.

In 1949, Einstein was concerned about a discovery by one of his close colleagues and friends, the Viennese mathematician Kurt Gödel, also at the Institute for Advanced Study at Princeton, where Einstein worked. Gödel found a disturbing solution to Einstein’s equations that allowed for violations of the basic tenets of common sense: His solution allowed for certain forms of time travel. For the first time in history, time travel was given a mathematical foundation.

In some quarters, Gödel was known as a spoiler. In 1931, he became famous (or, actually, infamous) when he proved, contrary to every expectation, that you cannot prove the self-consistency of arithmetic. In the process, he ruined a 2,000-year-old dream, dating back to Euclid and
the Greeks, which was to have been the crowning achievement of mathematics: to reduce all of mathematics to a small, self-consistent set of axioms from which everything could be derived.

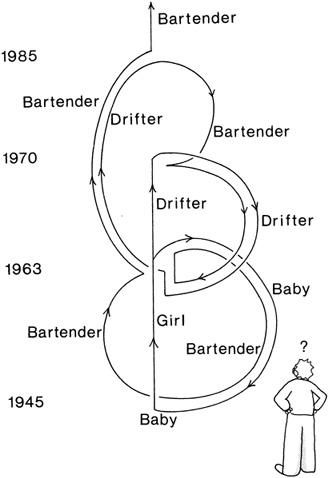
Figure 11.2. If time travel is possible, then our world line becomes a closed loop. In 1945, the girl is born. In 1963, she has a baby. In 1970, he is a drifter, who goes back to 1945 to meet himself. In 1985, he is a time traveler, who picks himself up in a bar in 1970, takes himself back to 1945, kidnaps the baby and takes her back to 1945, to start all over again. The girl is her own mother, father, grandfather, grandmother, son, daughter, and so on
.

In a mathematical tour de force, Gödel showed that there will always be theorems in arithmetic whose correctness or incorrectness can never be demonstrated from the axioms of arithmetic; that is, arithmetic will always be incomplete. Gödel’s result was the most startling, unexpected development in mathematical logic in perhaps a thousand years.

Mathematics, once thought to be the purest of all sciences because it was precise and certain, untarnished by the unpleasant crudeness of our material world, now became uncertain. After Gödel, the fundamental basis for mathematics seemed to be left adrift. (Crudely speaking, Gödel’s remarkable proof began by showing that there are curious paradoxes in logic. For example, consider the statement “This sentence is false.” If the sentence is true, then it follows that it is false. If the sentence is false, then the sentence is true. Or consider the statement “I am a liar.” Then I am a liar only if I tell the truth. Gödel then formulated the statement “This sentence cannot be proved true.” If the sentence is correct, then it cannot be proved to be correct. By carefully building a complex web of such paradoxes, Gödel showed that there are true statements that cannot be proved using arithmetic.)

After demolishing one of the most cherished dreams of all of mathematics, Gödel next shattered the conventional wisdom surrounding Einstein’s equations. He showed that Einstein’s theory contains some surprising pathologies, including time travel.

He first assumed that the universe was filled with gas or dust that was slowly rotating. This seemed reasonable, since the far reaches of the universe do seem to be filled with gas and dust. However, Gödel’s solution caused great concern for two reasons.

First, his solution violated Mach’s principle. He showed that
two
solutions of Einstein’s equations were possible with the same distribution of dust and gas. (This meant that Mach’s principle was somehow incomplete, that hidden assumptions were present.)

More important, he showed that certain forms of time travel were permitted. If one followed the path of a particle in a Gödel universe, eventually it would come back and meet itself in the past. He wrote, “By making a round trip on a rocket ship in a sufficiently wide curve, it is possible in these worlds to travel into any region of the past, present, and future, and back again.”
²
Thus Gödel found the first CTC in general relativity.

Previously, Newton considered time to be moving like a straight
arrow, which unerringly flies forward toward its target. Nothing could deflect or change the course of this arrow once it was shot. Einstein, however, showed that time was more like a mighty river, moving forward but often meandering through twisting valleys and plains. The presence of matter or energy might momentarily shift the direction of the river, but overall the river’s course was smooth: It never abruptly ended or jerked backward. However, Gödel showed that the river of time could be smoothly bent backward into a circle. Rivers, after all, have eddy currents and whirlpools. In the main, a river may flow forward, but at the edges there are always side pools where water flows in a circular motion.