Hyperspace (57 page)

1
. A. T. Schofield wrote, “We conclude, therefore, that a higher world than ours is not only conceivably possible, but probable; secondly that such a world may be considered as a world of four dimensions; and thirdly, that the spiritual world agrees largely in its mysterious laws … with what by analogy would be the laws, language, and claims of a fourth dimension” (quoted in Rudy Rucker,
The Fourth Dimension
[Boston: Houghton Mifflin, 1984], 56).

2
. Arthur Willink wrote, “When we have recognized the existence of Space of Four Dimensions there is no greater strain called for in the recognition of the existence of Space of Five Dimensions, and so on up to Space of an infinite number of Dimensions” (quoted in ibid., 200).

3
. H. G. Wells,
The Time Machine: An Invention
(London: Heinemann, 1895), 3.

4
. Linda Dalrymple Henderson,
The Fourth Dimension and Non-Euclidean Geometry in Modern Art
(Princeton, N.J.: Princeton University Press, 1983), xxi.

5
. Ibid. According to Henderson, “[T]he fourth dimension attracted the notice of such literary figures as H. G. Wells, Oscar Wilde, Joseph Conrad, Ford Madox Ford, Marcel Proust, and Gertrude Stein. Among musicians, Alexander Scriabin, Edgar Varese, and George Antheil were actively concerned with the fourth dimension, and were encouraged to make bold innovations in the name of a higher reality” (ibid., xix–xx).

6
. Lenin’s
Materialism and Empiro-Criticism
is important today because it deeply affected modern Soviet and Eastern European science. For example, Lenin’s celebrated phrase “the inexhaustibility of the electron” signified the dialectical notion that we find new sublayers and contradictions whenever we probe deeply into the heart of matter. For example, galaxies are composed of smaller star systems, which in turn contain planets, which are composed of molecules, which are made of atoms, which contain electrons, which, in turn, are “inexhaustible.” This is a variation of the “worlds within worlds” theory.

7
. Vladimir Lenin,
Materialism and Empiro-Criticism
, in Karl Marx, Friedrich Engels, and Vladimir Lenin,
On Dialectical Materialism
(Moscow: Progress, 1977), 305–306.

8.
Ibid.

9.
Quoted in Rucker,
Fourth Dimension
, 64.

10.
Imagine a Flatlander building a sequence of six adjacent squares, in the
shape of a cross. To a Flatlander, the squares are rigid. They cannot be twisted or rotated along any of the sides connecting the squares. Now imagine, however, that we grab the squares and decide to fold up the series of squares, forming a cube. The joints connecting the squares, which were rigid in two dimensions, can be easily folded in three dimensions. In fact, the folding operation can be performed smoothly without a Flatlander even noticing that the folding is taking place.

Now, if a Flatlander were inside the cube, he would notice a surprising thing. Each square leads to another square. There is no “outside” to the cube. Each time a Flatlander moves from one square to the next, he smoothly (without his knowledge) bends 90 degrees in the third dimension and enters the next square. From the outside, the house is just an ordinary square. However, to someone entering the square, he would find a bizarre sequence of squares, each square leading impossibly to the next square. To him, it would seem impossible that the interior of a single square could house a series of six squares.

1.
Jacob Bronowski,
The Ascent of Man
(Boston: Little, Brown, 1974), 247

2
. Quoted in Abraham Pais,
Subtle Is the Lord: The Science and the Life of Albert Einstein
(Oxford: Oxford University Press, 1982), 131.

3
. Normally, it is absurd to think that two people can each be taller than the other. However, in this situation we have two people, each correctly thinking that the other has been compressed. This is not a true contradiction because it takes
time
in which to perform a measurement, and time as well as space has been distorted. In particular, events that appear simultaneous in one frame are not simultaneous when viewed in another frame.

For example, let’s say that people on the platform take out a ruler and, as the train passes by, drop the measuring stick onto the platform. As the train goes by, they drop the two ends of the stick so that the ends hit the platform simultaneously. In this way, they can prove that the entire length of the compressed train, from front to back, is only 1 foot long.

Now consider the same measuring process from the point of view of the passengers on the train. They think they are at rest and see the compressed subway station coming toward them, with compressed people about to drop a compressed ruler onto the platform. At first it seems impossible that such a tiny ruler would be able to measure the entire length of the train. However, when the ruler is dropped, the ends of the ruler do
not
hit the floor simultaneously. One end of the ruler hits the floor just as the station goes by the front end of the train. Only when the station has moved completely by the length of the entire train does the second end of the ruler finally hit the floor. In this way, the same ruler has measured the entire length of the train in either frame.

The essence of this “paradox,” and many others that appear in relativity
theory, is that the measuring process takes time, and that both space and time become distorted in different ways in different frames.

4.
Maxwell’s equations look like this (we set
c
= 1):

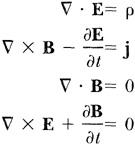
The second and last lines are actually vector equations representing three equations each. Therefore, there are eight equations in Maxwell’s equations.

We can rewrite these equations relativistically. If we introduce the Maxwell tensor
F
_μυ
= ∂
_μ
A
_υ
− ∂
_υ
A
_μ
, then these equations reduce to one equation:

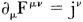
which is the relativistic version of Maxwell’s equations.

5.
Quoted in Pais,
Subtle Is the Lord
, 239.

6.
Ibid., 179.

7.
Einstein’s equations look like this:

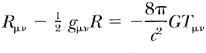
where T
_μυ
is the energy-momentum tensor that measures the matter-energy content, while R
_μυ
is the contracted Riemann curvature tensor. This equation says that the energy-momentum tensor determines the amount of curvature present in hyperspace.

8.
Quoted in Pais,
Subtle Is the Lord
, 212.

9
. Quoted in K. C. Cole,
Sympathetic Vibrations: Reflections on Physics as a Way of Life
(New York: Bantam, 1985), 29.

10
. A hypersphere can be defined in much the same way as a circle or sphere. A circle is defined as the set of points that satisfy the equation
x
²
+
y
²
=
r
²
in the
x-y
plane. A sphere is defined as the set of points that satisfy
x
²
+
y
²
+
z
²
=
r
²
in
x-y-z
space. A four-dimensional hypersphere is defined as the set of points that satisfy
x
²
+
y
2
²
+
z
²
+
u
²
=
r
²
in
x-y-z-u
space. This procedure can easily be extended to
N
-dimensional space.

11
. Quoted in Abdus Salam, “Overview of Particle Physics,” in
The New Physics
, ed. Paul Davies (Cambridge: Cambridge University Press, 1989), 487.

12
. Theodr Kaluza, “Zum Unitätsproblem der Physik,”
Sitzungsberichte Preussische Akademie der Wissenschaften
96 (1921): 69.

13
. In 1914, even before Einstein proposed his theory of general relativity,
physicist Gunnar Nordstrom tried to unify electromagnetism with gravity by introducing a five-dimensional Maxwell theory. If one examines his theory, one finds that it correctly contains Maxwell’s theory of light in four dimensions, but it is a scalar theory of gravity, which is known to be incorrect. As a consequence, Nordstrom’s ideas were largely forgotten. In some sense, he published too soon. His paper was written 1 year before Einstein’s theory of gravity was published, and hence it was impossible for him to write down a five-dimensional Einstein-type theory of gravity.

Kaluza’s theory, in contrast to Nordstrom’s, began with a metric tensor
g
_μυ
defined in five-dimensional space. Then Kaluza identified
g
_μ5
with the Maxwell tensor
A
_μ
. The old four-dimensional Einstein metric was then identified by Kaluza’s new metric only if μ and υ did not equal 5. In this simple but elegant way, both the Einstein field and the Maxwell field were placed inside Kaluza’s five-dimensional metric tensor.

Also, apparently Heinrich Mandel and Gustav Mie proposed five-dimensional theories. Thus the fact that higher dimensions were such a dominant aspect of popular culture probably helped to cross-pollinate the world of physics. In this sense, the work of Riemann was coming full circle.

14.
Peter Freund, interview with author, 1990.

15.
Ibid.

1
. Quoted in K. C. Cole,
Sympathetic Vibrations: Reflections on Physics as a Way of Life
(New York: Bantam, 1985), 204.

2
. Quoted in Nigel Calder,
The Key to the Universe
(New York: Penguin, 1977), 69.

3
. Quoted in R. P. Crease and C. C. Mann,
The Second Creation
(New York: Macmillan, 1986), 326.

4.
Ibid., 293.

5
. William Blake, “Tyger! Tyger! burning bright,” from “Songs of Experience,” in
The Poems of William Blake
, ed. W. B. Yeats (London: Routledge, 1905).

6
. Quoted in Heinz Pagels,
Perfect Symmetry: The Search for the Beginning of Time
(New York: Bantam, 1985), 177.

7.
Quoted in Cole,
Sympathetic Vibrations
, 229.

8
. Quoted in John Gribben,
In Search of Schrödinger’s Cat
(New York: Bantam, 1984), 79.

1
. Quoted in R. P. Crease and C. C. Mann,
The Second Creation
(New York: Macmillan, 1986), 411.

2
. Quoted in Nigel Calder,
The Key to the Universe
(New York: Penguin, 1977), 15.

3.
Quoted in Crease and Mann,
Second Creation
, 418.

4
. Heinz Pagels,
Perfect Symmetry: The Search for the Beginning of Time
(New York: Bantam, 1985), 327.

5.
Quoted in Crease and Mann,
Second Creation
, 417.