Mathematics and the Real World (45 page)
Read Mathematics and the Real World Online
Authors: Zvi Artstein

51. MATHEMATICS FOR COMPUTATIONS
In Assyria, Babylon, and Egypt, mathematics dealt only with calculations. These calculations were needed in building, agriculture, trade, and so on. As already mentioned (in section 6), there is no evidence that the mathematicians in those days invested time or effort in formulating or documenting the methods they used to solve problems, but it is clear that they were familiar with them and could draw an analogy from the solution to one problem to solve a similar problem. They passed this knowledge on by recording the actual problems they solved, either on clay or on papyrus. Thousands of shards and a number of papyri have survived and testify to this enormous accumulation of knowledge. They show many instances of different types of mathematical calculations. For example, shards have been found with multiplication tables inscribed similar to those used today. Others contain lists of numbers broken down into their factors, and the like. Some give clear indications that they were used in a lesson in mathematics. Others were apparently used by builders or traders, or even by
mathematicians carrying out calculations simply for their own amusement. Counting systems, including the choice of a base used to present the numbers, developed such that they simplified the writing of the numbers and also calculations, but there is no evidence of discussion of the methods themselves and the relation between the method and the calculations. To solve a new problem, the user had to analogize from among the collection of previously solved problems. This culture of calculation did not include abstract formulae or general methods that would help the user to solve new problems. Further evidence that mathematicians of that period did not deal with mathematics beyond the realm of calculations can be seen from the fact that there was no insistence on solutions being exact. Many of the Babylonian records have exercises in addition and factorizing numbers in which the results are just approximations of the correct solution. The approximation may have been good enough for the purposes for which the solution was used, but it would not meet standards of mathematical precision. We have commented previously that this need not surprise us. Generalization, per se, is not a characteristic that evolution has implanted in us, and hence it is not natural. Generalization and abstraction yield results after a long time, and the recognition of the importance of precision came about only in classical Greece.
The Greeks, while using mathematics as a means of expressing rules of nature and developing mathematical subjects with insistence on proofs, rules of inference, and so on, did not neglect the mathematics of calculations. They made great efforts to develop methods of calculation and also realized the importance of their formulation and documentation. Neither did they hesitate to develop new mathematics to help the efficiency of calculations. We will give two examples.
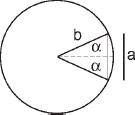
The first is trigonometry. The relation between the length of chords of a circle and its diameter and the use of these relations in geometric constructions are attributed to Thales of Miletus, since then the study of the geometry of circles and their chords has made great progress. Later, the use of trigonometric sizes for calculations developed, motivated by the interest in astronomy. The sine of the angle alpha was described then as the length of the chord
a
divided by twice the radius,
b
(see the diagram). (The equivalent definition that we learn at school, and which relates to the ratio of two sides of a right-angled triangle, was adopted only in the eighteenth century.)
The impact of the study of chords of circles was also evident in methods of calculation. Ptolemy presented many trigonometric relations in his books, but they always related to right-angled triangles. Menelaus of Alexandria (70–140 CE) extended the rules of plane trigonometry to spherical trigonometry and used the methods he developed for calculations in astronomy. Menelaus, Ptolemy, and their colleagues relied on tables of trigonometric quantities. Apart from the fact that the lists in these tables related to lengths of chords of circles, the tables were similar in structure to those included in mathematics textbooks that were in use until quite recently. With the advent of computers it became more efficient to recalculate the required quantity than to look in the tables.
The source of another system of the mathematics specific to calculation purposes can be found in the dichotomy paradox of Zeno of Elea (490–430 BCE). This paradox, one of four paradoxes of motion, claims that anyone wanting to reach a certain place can never reach it. First he has to cover half of the distance, then another quarter of the distance, then an eighth, and so on, ad infinitum. Thus he can never arrive at his destination. Aristotle referred to the philosophical aspect of the claim and its implications for motion, but as far as the paradox itself was concerned, he stated that the time of each successive stage also gets smaller, and the target will be reached. However, he did not include a method for calculating the time required. Eudoxus's exhaustion method (see section 7) discussed a similar problem and showed how to calculate areas by dividing them into smaller and smaller subareas. Archimedes improved the method, as we shall see.
The system was used later by Newton and Leibniz as the basis for the development of calculus.
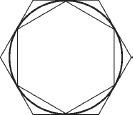
Archimedes's method was to enclose the shape whose area he wished to measure between two shapes whose areas are easy to calculate; for example, the circle in the diagram below enclosed by the two hexagons. When the difference between outer and inner enclosing shapes is small, the area of each is a good approximation of the area we wish to measure. To obtain an approximation even closer to the area of the circle in the diagram, the hexagons would have to be replaced by polygons with more sides. The more sides there are to the shapes, the closer the approximation.
Archimedes also referred to the concept of the limit. The areas obtained via the series of approximations that converge closer and closer to the sought area is called the limit and, according to Archimedes, is the right area. Newton and Leibniz extended the system beyond the method of calculation and made it a mathematical theory, a tool both for describing nature and for mathematical analyses and calculations. Archimedes developed the system as an auxiliary instrument for calculations. He also presented the computational concept of an “approximation as close as we wish.” There is no possibility of presenting the area of a circle with radius 1 as an exact decimal number (the area of a circle with radius
r
is
πr
2
and
π
is an irrational number). We can, however, obtain as close an approximation as we like. That is, if you, the reader, wish to know the area of a circle with an accuracy of one millionth, I, Archimedes, can find it for you. If you wish to improve the accuracy to a level of one billionth, I can calculate that as well; in fact, I can do so to any degree of precision. Note that such a stipulation, that is, “for any degree of approximation I can find a solution with that degree of precision,” is based on the logic developed by the Greeks.
Since then, the concept of an approximation as close as we wish has become the cornerstone of modern computations. As is the case with most contributions of the Greek scientists, no original writings of Archimedes have survived, and we must rely on copies of them accompanied in the spirit of that era by corrections and interpretations. One of the well-known interpreters of Archimedes was Eutocius, who was born in about 480 CE and worked in Ashkelon, a city in Israel.
Calculation methods continued to improve throughout the development of mathematics. Another contribution that made calculations easier was the invention, or discovery, of logarithms. The system was developed by John Napier (1550–1617), a Scottish mathematician who also dealt with physics and astronomy, and in keeping with the spirit of the time, also astrology. Napier developed logarithms to make calculations easier. It was only later that the ingredients of the system, that is, the logarithmic function and the exponential function, played a major role in the description of nature.
The logarithm of a positive number, say
N
, to a given base, say
a
, is the number
b
that satisfies
a
b
=
N
. This is denoted by log
a
(
N
) =
b
. Any number bigger than one can be chosen as a base. Napier himself defined a function very similar to the logarithmic function, whose values do not depend on the selected base. It was discovered very soon that calculations become much simpler if the number
e
is chosen as the base, called the natural logarithm. Its value is approximately 2.71828 (it is an irrational number, so it cannot be given exactly as a decimal number). The function is shown as ln(
N
) =
b
, that is, the base
e
is omitted.
We will not go into the details of the calculations, but we will just note that the equality ln(
NM
) = ln(
N
) + ln(
M
) that derives from the laws of powers is the key to the efficiency of the system. This equality enables us to convert the multiplication of two numbers, say
N
and
M
, by finding the logarithms of
N
and
M
in a table of logarithms, adding them together (and the sum is the logarithm of
NM
), and then finding in the table the number whose logarithm is that sum. In that way we can convert the complicated calculation
N
multiplied by
M
to finding in a table of logarithms the values of ln(
N
) and ln(
M
), then adding the two numbers, then looking up in a table of logarithms the number whose logarithm is the
result of the summation of the two numbers that were added. As it is much easier to add two numbers than to multiply them, especially if they are large numbers, the system of logarithms simplifies mathematical computations. The calculation depends on finding the appropriate tables, but these tables can be produced once and then used for any calculation. Napier presented such tables of logarithms, and even in his days they were improved, and they were used from then until quite recently. That method of computation was part of the compulsory syllabus when I was a student in secondary school and then at university, and the log tables were study aids. Nowadays it is easier to press the appropriate button, and the electronic calculator will provide the result much faster and with greater accuracy than can be achieved by using tables.
Gauss made an important contribution to computation methods, in addition to his other contributions. One of his contributions, mentioned above (section 39) related to the asteroid Ceres, which was discovered in 1801 by Giuseppe Piazzi, an Italian astronomer from Palermo. The discovery of the asteroid aroused great interest, among other reasons because its position and size were consistent with the possibility that it was in fact a new planet, a possibility that several astronomers had indicated prior to its discovery. Within a few months, however, Ceres approached so close to the Sun that it could not be identified, and the few measurements that had been taken up until then were insufficient to enable the calculation of when it would reappear on the other side of the Sun. The young Gauss, then aged twenty-four, took this task upon himself. To carry out the calculations Gauss developed a special method, based on an approximation of Ceres's elliptical orbit by summing cyclical orbits given by trigonometric functions and then computing their parameters.