Pythagorus (31 page)

Boethius, probably a late medieval representation

He did not last long there. In 523, he was falsely accused of treason and the use of magic. Theodoric imprisoned him and executed him the next year, but not before Boethius in his prison cell had done his deepest thinking and most eloquent writing – a book redolent of Platonic ideas, called
Consolations of Philosophy
. Throughout the Middle Ages, Boethius was considered on the level of one of the church fathers, if not exactly one of them, but in this book he wrote not of the Christian command, but of the Pythagorean command, to ‘follow God'.

For centuries, medieval scholars in Latin Europe would know the Greek authors through the Latin translations and commentaries Boethius had written. In large part thanks to him and Macrobius, the flame of classical Greek philosophy was kept burning in the monasteries of the Middle Ages. Also because of Boethius, Nicomachus' version of neo-Pythagorean mathematics became the bane of every student's existence.

The impact in the Middle Ages of another of Boethius' books, a multivolume work called
De institutione musica
, was almost as great as that of his
De institutione arithmetic
, which preserved Nicomachus' mathematics. Islamic philosophers would refer to it when they wrote about music from a Pythagorean point of view, and it would become a staple when medieval educators adopted the Pythagorean quadrivium. The first three volumes of
De institutione musica
were probably a translation or close paraphrase of Nicomachus'
Introduction to Music
, since lost. The approach was Pythagorean, emphasising the importance of the musical ratios, linking specific notes of the scale to the Sun, Moon, and planets, and referring frequently to Pythagoras. Boethius divided ‘music' into three subjects:
musica mundana
was the harmony of the spheres,
musica humana
the relationship of music to the human soul, and
musica instrumentalis
what we normally think of as music.

In the sixth century, the old Roman Empire in the East had a new name, the Byzantine Empire, and was still alive and flourishing brilliantly. Greco-Roman civilisation had certainly not died there. Alexandria was a wealthy, thriving city, as were Jerusalem and Antioch; Constantinople had replaced Rome as the capital of the civilised world, and its emperor was for all intents and purposes the head of the Christian church. Before mid-century, the Byzantine general Belisarius drove the Vandals out of North Africa, conquered the southern part of Spain, and retook Rome. The Byzantine Empire soon held Ravenna – ending Theodoric's brief golden age there – as well as Genoa, most of Sicily, and southern Italy, including Calabria (the old Magna Graecia) which would not be lost until the middle of the eleventh century. However, the reconquest of Italy, rather than restoring prosperity there, destroyed what little was left. It was in the Near and Middle East and North Africa that the old traditions of teaching and learning continued, and where Christian scholars were carefully preserving ancient texts and knowledge of the ancient Greek language.

The preservation and treasuring of classical philosophy and learning would continue in those regions for many centuries, but not under the aegis of the Christian Byzantine Empire. In the seventh century, followers of Mohammed poured out of the east. In Syria and Egypt there was scarce resistance, and the great cities surrendered quickly with little damage when the conquerors assured the Jewish and Christian populations that they could continue as usual with their beliefs and worship. This was fortunate for still-existing ancient texts, which came into Islamic hands and were regarded as a precious heritage. By 718, the Arabs held all of Spain, where they would continue as a small but powerful elite, ruling in a manner that was astoundingly tolerant in religious matters and open to cultural influences from all over the Mediterranean and Islamic world.

In the monasteries of Christian Latin Europe, scholars eked out a meagre intellectual living on the works of Macrobius and Boethius and a few other classical Latin authors, copying and preserving them with excruciating care, occasionally hearing and hardly believing rumours that the lost literary and philosophical treasures of Greece and Rome still existed in a far-off place. But it was under the rule of Islam in the Middle East, North Africa, and Moorish Spain that most of the preservation of ancient knowledge and writings, and the development of newer mathematics and astronomy based on them, moved forward from the eighth century to the eleventh.

PART III

Eighth–Twenty-first Centuries A.D.

CHAPTER 14

‘Dwarfs on the shoulders of giants': Pythagoras in the Middle Ages

Eighth–Fourteenth Centuries

By the eighth century, the
book destined to be Ptolemy's most celebrated work had reached Baghdad. Islamic scholars translated it into Arabic, and
Almagest
, ‘The Greatest', was its ninth-century Arabic title. While Islamic mathematicians and astronomers were advancing beyond the methods and models of Hellenistic scholars, no one apparently questioned the Earth-centred model of the cosmos or seems to have been aware of Philolaus' Pythagorean ten-body model with the central fire and counter-earth. Al Fargani, a brilliant ninth-century Arab astronomer, estimated the sizes of the spheres in which the planets move and worked out relationships among their distances, but musical ratios were not part of his calculations or those of other Islamic astronomers. Those with an ear for Pythagorean harmony of the spheres in the Islamic world were men concerned with the effects of instrumental and vocal music on the health of the body and the well-being and morality of the human soul. They were following the lead of a ninth-century writer named Honein Ibn Ishak al-'Ibadi, or Hunayn.
1

The mission of the Bayt al-hikma, or House of Learning, an academy in ninth-century Baghdad, was to retrieve the knowledge of antiquity and make it available to readers in Arabic. Baghdad was a cosmopolitan city where ideas flowed freely and minority religions were regarded as no serious threat. Hunayn, though not a Muslim but a Nestorian Christian, was both a member of this academy and the chief court physician to the caliph.
[1]

Hunayn's fluent Greek made him useful for more than his medical expertise. He translated books from Greek into Arabic for Islamic patrons and into Syriac for Christians, and he also produced Arabic translations of the works of his ancient medical predecessor Galen, and of the Hebrew Scriptures (from a Greek version).

Curious about the way music affects the human body and psyche, Hunayn wrote the first known treatise on music in Islamic literature, full of Pythagorean/Platonic themes of unity, harmony, Forms, the estrangement of the soul from the divine, and the possibility of their eventual reunion. ‘Living in solitude, the soul sings plaintive melodies, whereby it reminds itself of its own superior world', he wrote, and described how life often works to seduce the soul away from this superior world. For him, music, rather than numbers, was the great underlying connector: ‘The excellence of music is evident by the fact that it appertains to every profession, like a man of understanding who associates himself with everybody.' Hunayn compiled a collection of aphorisms, anecdotes, letters, and excerpts from a variety of Greek sources that he titled
Maxims of the Philosophers (Nawadir al-falasifa)
.
2
He took these from compilers like Plutarch, not from the originals, but the excerpts frequently began with ‘Plato used to say', or ‘Aristotle said', or ‘Alexander asked Aristotle', invoking Archytas and Euclid as well. Numbers were involved in some of the excerpts, but no real mathematics.
[2]

Hunayn had a sense of humour:

Once a philosopher went out for a walk accompanied by his disciple. They heard a voice and a guitar. The philosopher said to his disciple: ‘Let us approach the guitar; perhaps we can learn some sublime Form.' But as they came closer to the guitar, they heard a bad tone and an inartistic song. The philosopher then said to his disciple: ‘The magicians and astrologers assert that the voice of an owl indicates death for man. Were this true, the voice of this man should indicate death for an owl.'
3

Some of Hunayn's collected aphorisms were later incorporated into a mammoth Islamic encyclopaedia that appeared about a hundred years after his own lifetime, produced by a tenth-century community known as the Ikhwan al-Safa', or Brethren of Purity, in Basra in southeastern Iraq. Like the scholars of Hunayn's House of Learning, the Brethren attempted to preserve all they could of the ancient scientific and philosophical material that had come into Islamic hands. Their chief undertaking was an encyclopedia called the
Rasa'il
, in fifty-two volumes. Its purpose was to cover human knowledge in its entirety. Some ancient books were paraphrased, but few passages were taken verbatim in translation. Instead, the
Rasa'il
was an extravagant re-envisioning of earlier doctrines, an example of a second phase of the work to which so many Islamic scholars were devoted. One of the greatest, Al-Kindi, described it as striving to ‘complete what the ancients have not fully expressed, and this according to the usage of our Arabic language, the customs of our age, and our own ability'.
4

The Brethren of Purity viewed all knowledge as a continuum of revelation taking place in all times and places and among all races and religions. Pythagoras, Plato, Abraham, Jesus, Mohammed, and the imams who succeeded Mohammed were all part of it. The Brethren put together a cosmology of their own having many interlinked levels of being, with ‘One God' whose holiness lived in all things. The highest destiny of a human was to rejoin his or her inner holiness to this One God. The
Rasa'il
wove together many aspects of the world – music, numbers, medicine, theology, astronomy, and other areas. The interlinking was based in a precise manner on numbers and music and conjured up a ‘unity', not as the Pythagoreans had done it but very much in the Pythagorean spirit and with them in mind. Referring to ancient ‘musician-philosophers' who had drawn a connection between the four elements – fire, air, water, and earth – the Brethren linked these with human health, the arrangement of the cosmos, and the four strings of an instrument called the
oud
:

This we have expounded in the treatise on arithmetic. In effect, the first string is comparable to the element of fire, and its sonority corresponds to the heat and its intensity. The second string is comparable to the element of air and its sonority corresponds to the softness of air and its gentleness. The third string is comparable to the element of water and its freshness. The fourth string is comparable to the element of earth and its sonority corresponds to the heaviness of earth and its density.
5

The link with the human body and physical and mental health, echoing Hunayn, had the sounds of the different strings producing different effects in those who heard them: ‘The sonority of the first string reinforces the humour of yellow bile, augments its vigour and its effect; it possesses a nature opposed to that of the humour of phlegm, and softens it.'
6
Unlike Hunayn, however, the Brethren included specific mathematics. In their arrangement of the cosmos, each of the four elements, plus something called frigidity, predominated in one of a set of nested spheres with the Earth in the centre. The size of each sphere, in relation to the next, was in the ratio of 4:3. Beyond the orbit of the Moon there was a ‘harmonious proportion that exists between the diameters of the spheres in which the planets move and those of earth and air'.
7

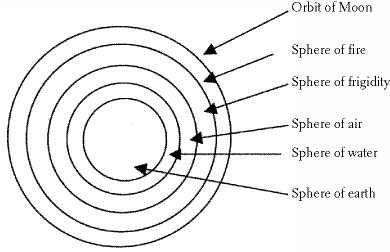
The Ikhwan al-Safa' or Brethren of Purity arrangement of the cosmos beneath the orbit of the Moon. This drawing shows the spheres, but not the exact proportions.

The Brethren made connections among the cube, the notes of the strings on the
oud
, and the relationships between the notes: The ancients, they said – continuing their reinterpretation of Pythagorean thinking and working Euclid into it as well – had a preference for the octave, because 8 was the first cube number (2×2×2). A cube has six sides and 6 is a perfect number.
[3]
All of a cube's sides are equal and all of its angles are equal, and

we have said that the more the created thing possesses the property of equality, the greater its eminence. It is for this reason that it was said in Euclid's last treatise that the form of the earth is probably cubic and that of the celestial sphere probably a dodecahedron defined by twelve pentagons.
8

The preference for ‘equality' calls to mind Archytas.

Also in the tenth century, when the Brethren of Purity were compiling their encyclopaedia, a Shiite
katib
(secretary) in Syria wrote a treatise in the same tradition. What seemed most significant to Al-Hasan al-Katib was the Pythagorean insight that numbers and the relationships between them were the key to human understanding of the universe. He reformulated this doctrine and applied it both to the human body and soul and to the cosmos: Three was the number of the simple consonances in music (fourth, fifth, octave) and also the number of the divisions of the soul (rational, sensible or sensitive, and natural or vegetative). Seven was the number of notes in the scale short of the octave and seven was also the number of elements of the rational soul: comprehension, intelligence, memory, deliberation, estimation, syllogism, knowledge. Different modes in music were equivalent to different virtues of the soul: justice – the mode of the index finger on the second string; good understanding – the mode of the open third string; purity – the middle finger on the third string; and so forth. In Al-Hasan's scheme, the movements and positions of the celestial spheres also had their equivalents in music, and the origin of the zodiac could be explained in similar terms. He wrote that he was indebted to Nicomachus of Gerasa for these ideas.

The sphere of the Zodiac is divided into twelve parts which represent the houses of the Zodiac. We believe that this division was established [or defined] thus because the number 12 is divisible into halves, thirds, and quarters. These are the elements which are found in the division of the complete system, because the last note of the octave is half the first (2:1), the note of the fifth is in the ratio of one and a half to it (3:2), the note of the fourth is in the ratio of one and a third to it (4:3).
9

In the parts
of Europe not under Islamic rule, populations in different areas spoke a great variety of vernacular languages and dialects, but Latin was the lingua franca that united scholars, who were almost without exception the only people who could read. As Boethius had feared, Greek had disappeared almost entirely. Little remained in Europe to be read in Greek anyway, since Greek manuscripts that at first had been preserved by Christians were now nearly all far away in Islamic lands.

However, Latin Europe did not languish in total intellectual darkness. Even in the ninth and tenth centuries, when Viking, Magyar, and Saracen invasions repeatedly wreaked havoc, scholars were carrying forward Pythagorean/Platonic ideas about numbers and music. Taking them in a different direction from their Islamic contemporaries, they explored the links between music and astronomy and inventively manipulated the numbers and mathematics of music and the cosmos.

Aurelian of Réôme (now Moutiers-Saint-Jean) was a contemporary of Hunayn; most of his writing dates from the decade 840 to 850.
10
The earliest medieval music treatise that has survived was his
Musica disciplina
, based in part on Boethius. Aurelian did know Greek and some astronomy and was knowledgeable about the movements of the planets and their periods.
[4]
He observed that the eight musical modes seemed to copy eight kinds of celestial motion. He wrote of instances when angelic music was audible on Earth, and about the Muses and the zodiac, though he had to be inventive to link eight musical modes with nine Muses. Aurelian followed the Pythagorean lead in more ways than his interest in the harmony of the spheres: He knew of the quadrivium that Plato learned from Archytas, and he was convinced that the truth of the universe lay in numbers.

These motions, then, of the stars are eight, seven of the planets and one of that which is called the Zodiac [the sphere of fixed stars], which all say make the sweetest harmony of song; that is, consonance. Even the Lord, in the reply that he made out of the whirlwind to Holy Job, called this the harmony of heaven.[
[5]
]

Writers about this art have discovered other things. They say that the whole theory of the art of music consists of numbers. They choose to divide philosophy into three parts, which in Latin are called the natural, moral, and rational parts. The natural part is given over to four sciences, namely arithmetic, geometry, music and astronomy. In these, numbers, the measurements of the earth, sounds, and the positions of the stars are examined, but their essence and their whole origin is in mathematics.
11