Simply Complexity (14 page)

Figure 4.2
shows what would happen in the case of only three bar-goers. In this example, history says that the correct decision will be to go to the bar. One bar-goer has
p
= 0 and hence always does the opposite of what history says, one has
p
= 1 and hence always does the same as what history says, and one has
p
= 0.5 and so always flips a regular coin to decide what to do. Depending on whether the outcome is heads, i.e. he goes to the bar, or tails, i.e. he doesn’t go to the bar, the number of people in the bar will be 2 or 1.

Notice how similar this is to thinking about arrangements of files among shelves – which is precisely why we went through the discussion of inanimate or non-decision-taking objects first, before looking now at decision-taking objects. Moreover, this similarity means that every type of behavior that we have seen emerge in
chapters 2
and
3
for collections of non-decision-taking objects, can also emerge in collections of decision-taking objects such as people – and more.

So what happens in this setup when we have lots of people? We can assume that everyone starts off with an initial value of
p
and that if they perform very badly over time, they will modify their
p
value in some way. Earlier we indicated how the effect of modifying
p
could be incorporated in a simple way – if a bar-goer finds
that his net number of losses minus wins becomes equal to d, he changes his
p
value. His personal tally of losses and wins is then reset to zero, and he uses his new
p
value until it too needs modifying – and so on. As long as his net number of losses minus wins is less than d, he will continue to use his existing
p
value.

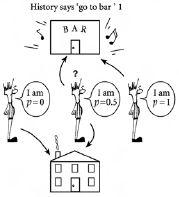
Figure 4.2
Just the three of us. The possible outcomes for a three-person population in which one person believes that history will always repeat itself (i.e.
p
= 1), one person believes that the opposite will always happen (i.e.
p
= 0), and one person continually flips between the two (i.e.
p
= 0.5). In this case, past history says that you should go to the bar. If the
p
= 0.5 agent’s decision is to go to the bar, then there will be two people in the bar – hence the bar would be overcrowded if the comfort limit is 1. If the
p
= 0.5 agent’s decision is not to go to the bar, then there will be one person in the bar – hence the bar will not be overcrowded if the comfort limit is 1.

Since we are trying to mimic the general diversity of a population, it makes sense to start off our collection of people with a range of
p
values. One simple way of doing this is just to randomly assign each bar-goer with an initial
p
number between 0 and 1. Then we let the system evolve as described in the previous section. The big
question is then this: what happens to this collection of bar-goers as time goes on? Given that no-one can win all the time, does the population gradually become so uncertain that they head toward
p
= 0.5? In other words, do people head toward completely random behavior?

Remarkably, it turns out that they do not. Pak Ming Hui of the Chinese University of Hong Kong has studied this problem in great detail with his own group of graduate students and in collaboration with my own group. It turns out that instead of heading toward random behavior, the bar-goers tend to head away from it toward the extremes. In other words, they become polarized into those who think that history will repeat itself, and those who think that the opposite will happen. The bar-goers who tend to shift opinions about whether to go with history or against it, tend to lose more and hence eventually change their
p
value. The ones with extreme values of
p
around 0 or 1 lose less and hence stay with those
p
values for a longer time. The net effect is therefore that the population of bar-goers tends to segregate itself spontaneously into two groups – one around
p
= 0 and one around
p
= 1. In other words, the population tends to split into a crowd that believes that history tends to repeat itself and hence sit around
p
= 1, and another crowd that believes that the opposite happens, and hence sit around
p
= 0. We call the former a
crowd
and the latter an
anticrowd
since they take the opposite action to the crowd.
Figure 4.3
shows this effect in terms of a diagram.

But maybe you are thinking that all this is just a quirk resulting from the way in which we have set up the problem? Maybe things change if we change the value of
m
, i.e. the number of past outcomes featured in the crib-sheet of public information? Or maybe it matters how people change their
p
value? Interestingly, it turns out that these things don’t matter – in other words, this surprising segregation of the population into a crowd and anticrowd is not a quirk. Instead, the emergence of the crowd and anticrowd turns out to be a very generic feature of such competitive games. In fact, it doesn’t matter what the value of
m
is, the same shape emerges as in
figure 4.3
. And since this bar problem is just one example of such decision problems, the emergence of crowds and anticrowds will arise in traffic, markets and all sorts of other systems. In other
words, it is a truly emergent phenomenon and is likely to be quite generic across different domains of application.

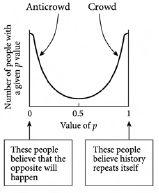
Figure 4.3
We are naturally divided. The final arrangement of a collection of people, in the case of a bar where the comfort limit is around half the number of potential attendees. This shows the emergent phenomenon of a crowd who think that history repeats itself, and an anticrowd who think that the opposite will happen. Hence the population polarizes itself into two opposing groups. This polarization of the population represents a universal emergent phenomenon. It will arise to a greater or lesser extent in any Complex System involving collections of decision-making objects such as people, which are competing for some form of limited resource.

The crowd-anticrowd phenomenon has a very important consequence. The fact that people in the crowd around
p
= 1 will typically be taking the opposite action to the anticrowd around
p
= 0, means that as far as the behavior of the population as a whole is concerned, the actions of such opposite personality types tend to cancel each other out – which is exactly what we had earlier claimed would happen. This becomes particularly important in a financial market setting, for example, since it means that the number of people deciding to buy at a given moment, will essentially cancel out the number deciding to sell. To understand the consequence of such a cancellation, just think of the housing market – if there are an equal number of buyers and sellers, the
price will not tend to move very much since supply and demand are balanced. There is no large excess of buyers tending to push the price up, nor is there a large excess of sellers tending to drive the price down. The resulting market will therefore tend to have small price-changes and hence a small volatility, or small fluctuations.

We have uncovered a truly remarkable effect. Even though there is no communication between the people in the game, and even though the game is competitive, the fact is that the system as a whole manages to self-organize itself in such a way that the fluctuations are smaller than for the case where everyone tosses a coin. More generally if we assume that fluctuations are bad for the system in some way, then we have shown that through competition the system as a whole does better than if the individual objects were to have behaved independently (i.e. by tossing a coin). The combination of competition for a limited resource and the fact that the people all receive the same sort of feedback, has given rise to a system which appears to be controlled by an “invisible hand” – but isn’t. Looking back to the engineering applications mentioned in
chapter 1
, we can see why such self-organized control via competition and without the need for any communication or collaboration between the objects, would be so interesting for engineers. It offers them the possibility of mimicking the controlling effect of an “invisible hand” without the hassle of having to build or maintain a central control unit. In other words, they can remove potentially harmful or dangerous fluctuations in a system, simply by making the individual components competitive.

Even if we change the form of the public information being fed back to the agents – in other words, the crib-sheet concerning the past outcomes – the result is the same as long as the information that all the people receive is the same. In short, it doesn’t matter whether the information is indeed past information or is instead someone’s prediction, or a radio announcement, or a rumor, or even some false information. The fact that everyone receives the same information, and hence reacts to it using their respective
p
value, means that everyone is effectively joined together by this common information – regardless of where it came from, and
regardless of whether it is right or wrong. Hence the feedback takes the form of common information, but it doesn’t matter whether the actual information fed back is correct or not – it just matters that everyone receives the same information.

So far I haven’t mentioned how the value of the bar’s comfort limit
L
affects the results, or how the value of the net losses
d
might change things. Again it turns out that these don’t have a great effect. As long as
L
isn’t so close to the number of potential attendees
N
that the competition effectively goes away, then the same segregation into crowds and anticrowds will also arise. The only thing which will disrupt the formation of crowds and anticrowds is if we make the penalty for losing outweigh the reward for winning. This effectively changes the whole game since people will then tend to change their
p
value so rapidly that the population never settles down to a steady situation. By contrast, making the reward for winning outweigh the penalty for losing, does not disrupt the emergence of the crowd-anticrowd phenomenon.

We just found that the population self-segregates by moving toward the extreme
p
regions. People who stick to the same type of decision in every turn therefore perform better than the uncertain people who choose randomly in each turn. We can understand this effect by again considering just three people. In fact we will go one step further and also only consider three
p
values:
p
= 0 corresponding to always going against the public information,
p
= 1 corresponding to always going with the public information, and
p
= 0.5 corresponding to someone being so cautious that they effectively flip an ordinary coin in order to decide. Let us suppose that for this problem of three bar-goers, the comfort limit is one. In other words,
N
= 3 and
L
= 1 which means that there are more than twice the number of potential attendees as there are seats in the bar – so this certainly embodies the notion of limited resources.

If we imagine the situation in which all three people have
p
= 1, then they all make the same decision and hence take the same
action. Therefore all three people either go to the bar and it is overcrowded, hence they lose, or they all stay away and the bar is undercrowded, and hence they lose again. So this arrangement with them all having
p
= 1 is unlikely to last very long. Likewise, the arrangement with them all having
p
= 0 is equally unfavourable, and hence also unlikely to last very long. If on the other hand they all have
p
= 0.5, then there is at least a chance that one person will win by having two people throw a heads and one throw a tails, or vice versa. However there is also the possibility that they all throw a heads, or all throw a tails, and hence all take the same decision and hence lose once more.