The Calendar (24 page)

Al-Khwarizmi wrote out the oldest surviving
zij--
set of astronomic tables--in the Arab world, much of it based on Indian charts possibly brought to Baghdad by Kanaka. This
zij
later made the journey to Spanish Cordoba and onwards to the rest of Europe, where a Latin translation made in 1126 became one of the most influential works on astronomy in medieval Europe.
Perhaps most important of all was a small booklet al-Khwarizmi penned in 825. Called
Algoritmi de numero Indorum
when it was later translated into Latin, this short treatise detailed something the great sage of Baghdad apparently picked up from reading Brahmagupta: the numerical system of the Indians--the nine symbols and a placeholder called
sunya.
Amazed by the usefulness of these simple symbols and of positional notation he demonstrated in his pamphlet their superiority to the Greek numbers then used in Baghdad, and to the cruder Bedouin numbers the Arabs had brought with them from the desert. At the time he wrote his booklet the ‘new’ Indian symbols looked something like this:*
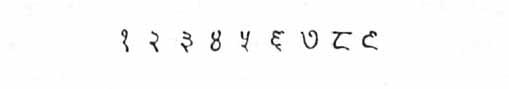
*No one knows what the symbols looked like in Al-Khwarizmi’s booklet because no original has survived in Arabic. The only extant copies are Latin translations.
Later Arab mathematicians expanded on the system described in al-Khwarizmi’s pamphlet and on the Indians themselves to take the Hindu idea of
sunya
--the Arabs’
cifra,
our
zero--
and use it not merely as a placeholder, but as a number like any other in certain calculations and equations. They also made a mathematical leap that the Indians did not, applying the system of positional notation to create decimal fractions--the first of which appear in an obscure book by an otherwise unknown Syrian mathematician named Abul Hassan al-Uqlidisi in 952 or 953. These discoveries made it possible just before the end of the first millennium of the Christian era to actually write out the number that represent the true solar year--365.242199 days--though as of yet no one had been able to come up with such an exact astronomic value. It also would have been written without the dot for the decimal point, which was added much later.
Al-Khwarizmi’s contemporaries in Baghdad were delighted with his little book. Used to a dizzying rush of new knowledge in this era of learning and scholarship, they quickly dropped the old methods of counting and embraced the new--which greatly accelerated the development of mathematical theory that would lay the foundation for modern science, including the reform of the calendar.
Scholars in Damascus to the west began using the new numbers just a few years later, but this invention took almost a century and a half to make the long journey to Spain, Sicily and other, more distant outposts of Islam. It took longer still to make the leap across the borders to a conservative Europe largely uninterested in new ideas, particularly those connected to a people they considered heathens in league with the devil.
Al-Khwarizmi was hardly the only genius at work in the Arab world during its glory years between the founding of Baghdad as the Abbasid capital in 763 and the final dissolution and fragmentation of the Islamic empire in the 1200s and 1300s. It is impossible to mention all of these, though a handful stand out above the rest in terms of the calendar. These include another denizen of the House of Wisdom born around the time of al-Khwarizmi’s death, Abu Allah Mohammed Ibn Jabir al-Battani (c. 850-929), known in Europe as Albategnius. In a book called
On the Motion of the Stars
he expounded on Indian trigonometric methods to show that the distance from the earth to the sun varies during the year, something we now know happens in part because the earth’s orbit is elliptic. Al-Battani also refined values for the length of the year by comparing it with calculations made by Ptolemy in 139. He came up with a figure that was 23 minutes too short--but that was because Ptolemy had placed his equinox a day late. Had Ptolemy been correct, al-Battani’s year would have been only half a minute short.
Half a century later another Arab astronomer, Abu ar-Rayhan Mohammed ibn Ahmad al-Biruni (973-1048), was born in central Asia. There he thrived despite the growing instability in the region as the Abbasid caliphate collapsed and its territories fragmented into shifting emirates ruled by local shahs and warlords.
Before the age of 30, in the midst of wars between rival kings, al-Biruni was able to make extensive observations of equinoxes and to travel to and fro taking highly accurate measurements of latitude. Also before turning 30--even as he was forced at times to go into hiding because of politics--he managed to write at least eight works. These included a treatise on timekeeping, a timeline of past events dated according to the Moslem calendar and arguments for and against the earth’s rotating on its axis, taking up the debate of Aryabhata versus later Indian astronomers.
Al-Biruni later became a diplomat for one rival shah and was imprisoned by another, though he was eventually allowed to continue his work as he followed an invading Moslem army into India. There he learned Sanskrit and studied every ancient text he could find, compiling his findings into a book called
India.
This offers a remarkably candid and critical analysis of Hindu mathematics and the
siddhantas.
In his late sixties al-Biruni wrote a study on the specific gravity of gems; at the age of 80 he wrote an alphabetical guide to 720 drugs, listing each according to their names in five languages.
The year al-Biruni died yet another Arab scholar and poet was born, Umar ibn Ibrahim al-Khayyami (c. 1048-1131)--known in the west as Omar Khayyam. Admired today outside of the Arab world exclusively as one of the greatest Islamic poets, Omar Khayyam was much more. Prolific in a number of fields, in mathematics he greatly expanded on al-Khwarizmi’s algebraic principals and on Euclid’s geometry; as an astronomer he spent 18 years working in an observatory in Isfahan, 200 miles south of modem Teheran in Iran, where among other things he measured the solar year at 365.24219858156 days. This was both accurate and overly precise considering the gradual slowing of the earth’s rotation. Omar Khayyam also devised a solar calendar with eight leap years of 366 days every 33 years--a slightly unwieldy system that nonetheless was more accurate than the Gregorian calendar. Apparently he proposed his new calendar as a reform to his local shah in 1079.
In one of his famous verses from
The Rubaiyat,
Omar Khayyam offers a poet’s assessment of what it means for a scientist to try to measure time--and the arrogance of those who blithely count and add and take away days on a calendar:
Ah, but my calculations, people say,
Have squared the year to human Compass, Eh?
If so, by striking from the calendar
Unborn tomorrow and dead Yesterday.
Another scholar working in the Islamic world, the Jewish astronomer Abraham bar Hiyya ha-Nasi (1070-1136), wrote in Barcelona the first Hebrew work devoted exclusively to the study of the calendar, including a prediction based on the Torah of when the Messiah might appear. Yet another astronomer appearing very late in the classic Arab era was Ulugh Beg (1394-1449), the ill-fated son of a shah, who briefly ruled Samarkand and was put to death by his own son during a coup. Ulugh Beg gave a measurement for the length of the year that came to 365 days, 5 hours, 49 minutes and 15 seconds--just 25 seconds too long.
Still, the Arabs came very close to calculating a true value for a year they did not use in their own religious calendar, a measurement few Europeans at the time even cared about. Even those who did care struggled with crude and incomplete formulas and data, a situation that seemed all but hopeless--and might have remained so if not for the eruption of learning out of Baghdad and other Islamic centres, a wave so powerful that it reached beyond even the distant rim of what was then the civilized world.
10 Latinorum Penuria (The Poverty of the Latins)
Why, as Bede himself admits . . . does a full moon appear in the sky in most cases one day, and in others two days, before the computed date?
Hermann the Lame, 1042
No one in Baghdad during the heady days of al-Khwarizmi could have guessed that their work would help spark a revival of learning in Europe. A traveller trekking from the caliph’s court to Aachen in the year 800 would have laughed at the idea that these foul-smelling
barbari,
ruled by an emperor who could not write, whose scholars copied old manuscripts rather than reading them, and whose mathematicians still counted with their fingers, would four centuries later produce a Roger Bacon. And three centuries after that a Copernicus.
Such a traveller would marvel at a people who had forgotten the mathematics, science and philosophy first conceived by ancients from whom they traced their own cultural roots. He also would have smiled at the irony, if he had been able to predict the future, of a people who would one day rediscover the ancient knowledge they had lost in part from Arabic translations of the original European texts.
At first the process of transferring the concepts crucial to Europe’s reawakening was almost imperceptibly slow. In 800 our adventurous Arab would have found at best several hundred ancient texts at Charlemagne’s court, and a castle full of half-educated Franks still in awe of Bede. A scholar from Baghdad--or Damascus--arriving in Latin Europe a century later, in 900, would have seen little difference. Even another century after that, in 1000, he would have witnessed only a few stirrings. Not until 1100 would our original traveller’s great-great-great-great-great-great-great-great-grandson see any significant change, three centuries after Charlemagne tried--and failed--to rejuvenate learning in Europe.
Visitors checking the status of Latin time reckoning would have discovered roughly the same progression--computists in their monasteries during the 800s still worrying over lists of saints’ days, updating Easter tables and spending lifetimes trying to devise arcane systems for better measuring time. In Frankland an intrepid Arab traveller might have met the teacher, theologian and scholar Rabanus Maurus (c. 780--856), a student of Alcuin and a prolific writer who spent many years of his long life fussing over how to divide the hour into ever smaller units: a useful idea, except that one has to ask why anyone in the ninth century would need to use, say, his
atom,
which he declared to be 1/22560 of an hour. Also, how would one measure the passage of such an infinitesimal moment of time with a water clock?
Other time reckoners during this period are now as notable for their unusual names as for their painstaking labours on
computus
and the calendar. They include three time reckoners whose work spanned the mid-ninth to the mid-eleventh centuries, all named Notker, and all who lived in the same Swiss monastery at St Gall near Zurich. These were Notker the Stammerer, Notker the Peppercorn and Notker the Thick-Lipped.
The 900s were little better than the 800s, with one major exception: a monk named Abbo of Fleury (945-1004), who advocated the use of water clocks that were more accurate than the sundial used by monks since before Bede. This allowed him to make slightly more accurate measurements than the venerable one for days, months and years. Abbo also proposed a change in Dionysius Exiguus’s chronology using
anni Domini
, substituting the old Latin style of passing from year 1 to year-1 to a timeline that added a place-holder in the zero position. To designate this ‘new’ year he used the symbol for null, since zero itself had not yet reached Europe. This suggested change was ignored, however. So was his idea that the date for Christ’s death as calculated by Dionysius was incorrect by some 20 years. But Abbo was an anomaly in a field that was becoming wearisome by the year 1000 with its rehashing of the same old formulas and arguments.
The last important work done in the traditional mould of
computus
and time reckoning was authored by yet another scholar-monk with an unflattering name, Hermann the Lame (1013-1054) of Reichenau, in western Germany near the border with Switzerland. Insisting early in his life that all scientific conclusions should be supported by ‘the insuperable truth of nature’--an astonishing admission in his day--Hermann used the recently arrived astrolabe and a special column sundial that he invented to compare what he saw in the sky to the fixed numbers used for centuries by computists. The first time reckoner since Bede to trust observation, he verified that the Church’s calendar--including Easter and many feasts and saints’ days--was out of sync with the cosmos. ‘Whence comes the error that the real age of the moon so often does not correspond to our reckoning,
computus
or the rules of the ancients. . . ?’ he asked in 1042.
Hermann’s frustration was compounded by his repeated attempts to correct Bede and other computists, all of which failed to match up with what he saw in the sky. This left the lame monk of Reichenau wondering towards the end of his short life--he died at age 41--if the centuries-old tradition of
computus
and time reckoning was hopelessly flawed, based on erroneous assumptions about the movements of the sun, moon and stars. But neither Hermann nor anyone else was willing to take this a step further and challenge the Church in an era when questioning St Peter’s was the same as doubting the Lord.