The Calendar (35 page)

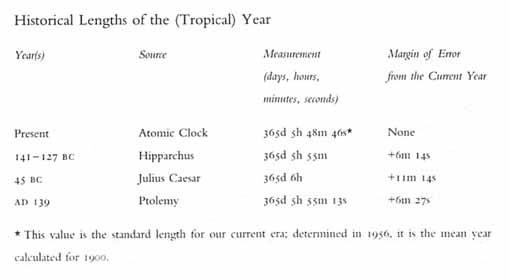
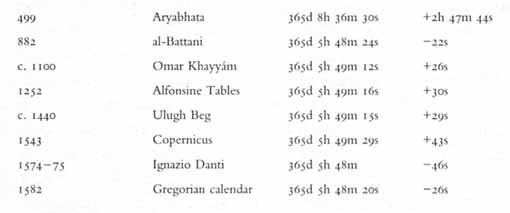
Once Lilius had decided on his mean year, he pondered the next crucial problem of reform: how to close the gap between Caesar’s year and the ‘true’ year. This meant comparing the Alfonsine year of 365 days, 5 hours, 49 minutes and 16 seconds to the Julian year of 365 days, 6 hours. The Alfonsine runs short of the Julian by 10 minutes 44 seconds--equal to a day lost every 134 years.
Lilius seems to have tried different ideas to work this cumbersome measurement into a simple formula for dropping an appropriate number of leap days from the calendar. He rejected the long-standing proposal advocated by Bacon and others to drop a day roughly every 134 years. Instead Lilio took as his inspiration the simplicity of the Julian leap-year formula, with its easy-to-remember four-year rule, hoping to come up with a similarly convenient dictum to solve the Julian gap.
As the good doctor tinkered with various solutions shortly before his death, he discovered that the gap amounted to three days gained against the true year every 402 years (134 years x 3). This he rounded off to three days every 400 years, a more accessible number that became the basis for the leap-century rule--which drops three days from the calendar every four hundred years by cancelling the leap year in three out of four century years. This formula, based on tables not entirely precise and a base number that is rounded off, ended up being remarkably accurate, running ahead of the seasons by only one day every 3,300 years.
Lilius also proposed two well-known options to recoup the days already lost due to the drift of the Julian calendar, which he thought should be cut by ten days to restore the equinox to the time of Nicaea. He suggested making up the days either by skipping 10 leap years over the course of 40 years, or--more radically--by removing ten days all at once.
The other big problem for Lilius and the calendar commission was repairing the Catholic lunar calendar used to determine Easter. Indeed, for the pope and other Christians the project of cinching up the solar calendar--and restoring the spring equinox to its proper place in the tropical year--was never an end in itself, but part of a religious fix required to restore the Feast of the Passion to its ‘proper’ date.
Easter, of course, is supposed to fall on the first Sunday after the first full moon after the spring equinox--a seemingly straightforward formula, except for the ancient problem that the moon and sun do not match up in their respective years. To compensate for this Christian time reckoners had long used the 19-year Metonic cycle--which theoretically brought the sun and moon into sync because every 19 years of solar time equalled 235 lunar months.
Well, almost. In reality the moon’s cycles run roughly an hour and a half behind the 19-year solar cycle, a mismatch that had been alarming computists and astronomers for some time.
Lilius calculated that the lunar-solar gap equals about 1 hour 27.5 minutes, which meant that the moon was drifting against the Church’s lunisolar calendar by a whole day every 312.7 years. By the 1570s this error had amounted to more than four complete days.
To halt this lunisolar mayhem, Lilius and the commission scrapped the old Metonic assumption that the phases of the moon, particularly the critical full moon, always matched up in the 19-year cycle with the solar year. Instead Lilius concentrated on trying to work out a new method for keeping the lunar calendar from sliding a day every 312.7 years.
Again, this was no easy task, given that 312.7 is hardly an easy number to divide into a Gregorian calendar of 365 days, 5 hours, 48 minutes and 20 seconds. But once more Lilius came through, with a simple discovery that eight periods of 312.7 years equal almost 2,500 years--a number that can be divided almost perfectly into seven periods of 300 years plus one period of 400 years. This was Lilius’s lunar solution: dropping one day from the lunar calendar every 300 years seven times, and then an additional eighth day after 400 years. For simplicity’s sake Lilius and the commission again proposed making the corrections and dropping the days at the end of appropriate centuries.
Lilius’s manuscript was initially received with some doubts and resistance, but soon it became the panel’s lead proposal as Clavius and company studied it and sent it to various experts for comments. One so-called expert, Giovanni Carlo Ottavio Lauro, at one point seems to have tried to slow up the review process by taking Lilius’s manuscript--and holding it for several months. Supposedly this was to make unspecified ‘corrections’, though Lauro actually used the time to delay action so that he could finish his own proposal. His tactics so infuriated Lilius’s supporters on the commission that they appealed directly to the pope, asking that the manuscript be returned--which it was--and the ‘chimeras’ of Lauro be ignored.
Lilius’s solution won out at last when the pope issued on 5 January 1578 the
Compendium
of the doctor’s manuscript to universities, heads of state and important prelates for their comments. The
Compendium
was sent rather than Lilius’s much longer manuscript to save time now that calendar reform fever had struck Rome--or at least the small group of people who cared about such matters in the Eternal City. It also allowed the calendar committee to add its own remarks and amendments, which Clavius later says were minimal. The 20-page
Compendium
was written by the commission member from Spain, Pedro Chacon, presumably with input from Lilius’s brother, Antonio.
After the publication, more comments poured into the commission. It received a vigorous response compared to past reform efforts, such as the one initiated earlier in the sixteenth century by Paul of Middelburg. This time the
Compendium
attracted dozens of letters, still preserved in the Vatican. Most simply gave their nod of approval; others contained comments, proposals and counterproposals, some of them fascinating. The court mathematician for the duke of Savoy, Giovanni Battista Benedetti, made a number of suggestions in an April 1578 letter--including a calendar correction of 21 days, which would land the winter solstice on the first of January. Benedetti further proposed changing the length of the months to coincide with the presence of the sun in each of the 12 zodiac signs. Other commentators advocated various dates for the equinox and complained about using a mean for the length of the year. Some went to the trouble of publishing their alternative plans and circulating them, hoping to get a hearing with the commission and the pope.
Royalty also responded. For instance, King Philip II of Spain, in a short letter signed with a flamboyant
El Rey,
‘The king’, approved of the plan, but insisted that the equinox be kept on 21 March--out of deference for Nicaea, but also for the practical reason that a great expense would be spared if the date did not have to be changed in mass books and breviaries.
The complaints of astronomers and other scientists would continue over the next several decades as the new calendar took hold. Most agreed with the technical side of the reform, including the Protestants Tycho Brahe and Johannes Kepler. Both found the reform scientifically sound and the best they had seen. Brahe from the beginning dated his letters using the new calendar, and Kepler in a posthumous article offered his arguments in the form of a dialogue between a Protestant chancellor, a Catholic preacher and an expert mathematician. In the end he concluded that Easter, which was causing so much consternation among opponents and proponents of the calendar, ‘is a feast and not a planet’. In 1613, Kepler argued in support of the reforms, but failed to persuade the Protestant sovereigns, a resistance that lasted until 1700. Even then Kepler’s own Rudolphine Tables were substituted for the Gregorian values when determining Easter. In some years, this caused Germany to celebrate Easter on a different day than Catholics and other Protestants.
A great many astronomers found fault with the new calendar, including several mathematicians in Prague who refused to help the bishop there revise the calendar of feasts because they claimed to find the science unsound. Others disagreed, sometimes vehemently, for religious reasons. These included the Protestant astronomer Michael Maestlin (1550-1631), a professor at Tubingen in southern Germany and one of the teachers of Johannes Kepler. He insisted that the pope had no authority to institute such a reform, and also criticized Gregory for calling the new calendar ‘perpetual’, because this denied the coming of the last Judgment. This argument was later refuted by another German defender of the calendar, who suggested that by Maestlin’s reasoning people should also stop building houses.
Maestlin and others repeated criticisms that the reform should adhere more closely to the true movements of the sun (i.e., the earth) and moon. They complained about the methods used to determine Easter in the lunar reforms, worried over whether the equinox under the reform would always fall on 21 March and challenged the sources for the length of the year. Many astronomers and mathematicians--including several assigned by monarchs and bishops to prepare the reforms for public dissemination--not only offered criticism but published their own solutions, sometimes side by side with the new calendar, to the confusion of anyone trying to understand the pope’s reforms.
Other astronomers, led by Christopher Clavius, defended the new calendar. In 1595 he wrote a refutation of Maestlin, directed at the calendar’s many critics, called
Novi calendarii Romani apologia, adversus Michaelem Maestlinum--
’Defence of the new Roman calendar, in reply to Michael Maestlin.’ He explained, among other things, why the commission adopted a system of mean rather than absolute motions.
Clavius also defended the use of a mean by pointing out that it was impossible for all Christians to celebrate Easter at exactly the same moment given the spread of Christians across several meridians. In 1606 Clavius answered his critics in the 800-page
Explicatio
(Explanation). In all, Clavius penned six treatises on the calendar, characteristically well-reasoned and scientifically sound documents that went a long way towards quieting the criticism and smoothing the way for reform in countries that initially hesitated to go along with the new calendar.
One of the most well-known scholarly critics of the calendar was a bitter rival of Clavius, the French scholar and Calvinist Joseph Justus Scaliger (1540-1609). He found the reform littered with supposed errors and even stooped to name-calling, referring to Clavius as a ‘German fat-belly’. But this did not keep Scaliger from later using the Gregorian system for his most famous project: creating a timeline of historical events according to the rules of astronomy. This was a monumental task, one that modernized the old medieval preoccupation with chronology and brought together all of the historical timelines and descriptions of events he could find. Indeed, he and Clavius were not so far apart in their respective tasks, the portly German setting out to align the calendar as closely as possible with the movements of the sun and moon, and Scaliger trying to get the past and future to correspond with a generally accepted standard. The year after the calendar reform Scaliger published
Opus de emendatione tempore
(1583), establishing chronology as a science.
Scaliger invented his own chronological calendar: the Julian day calendar, an ingenious if complex system that does not use individual years at all, but a cycle of 7,980 astronomic years that counts a day at a time, with no fractional days, no mean year and no leap years. He came up with his number by multiplying three chronologic cycles: an 18-year solar cycle, a 19-year lunar cycle, and the 15-year indiction period used by the Romans. All three cycles began together at the same moment at the start of his ‘Julian cycle’, but would not converge again until the end. This was useful for anyone trying to create a uniform timeline, since the date from any one of the three base cycles could be translated into the two other cycles.
This may sound far too obtuse for the average person. However, Scaliger’s calendar lives on today among astronomers, who do not need a calendar based on a mean of the tropical year but one that is astronomically exact. How else could one properly measure the time between, say, two appearances of the comet Hale-Bopp, or two pulses of a quasar? Scaliger began his Julian cycle at noon on 1 January 4713 BC, which he based on calculations concerning Creation.