The Calendar (34 page)

The scholar-scientists included the Dominican friar Ignazio Danti (1536-1586), the second most famous commission member after Clavius. A mathematician, astronomer, cartographer and artist, Danti was a professor of mathematics at Pisa and later at Bologna.
Summoned to Florence he also worked on astronomic projects under Grand Duke Cosimo I (Cosmos de Medici), preparing maps, an enormous terrestrial globe and instruments he used to observe the vernal equinoxes in 1574 and 1575. From this he came up with the length of the year as 365 days, 5 hours and 48 minutes. Comparing this to Ptolemy’s erroneous calculation of 365 days, 5 hours and 55 minutes, Danti joined Copernicus and other astronomers by concluding that the tropical year was variable. After a falling-out with Cosimo’s son, Danti relocated to Bologna, where he measured the solstices in 1576 with a gnomon he built in the church of St Petronius. He used this data to confirm the error in the Julian calendar and its drift against the true year.
In 1580 Danti was summoned to Rome by the pope to join the commission, and also to design the frescoes and astronomic instruments in a new building devoted to astronomy and to calendar reckoning. Known as the Tower of the Winds, this 240-foot tower north of St Peter’s dome and above the Vatican archives, was built between 1578 and 1580 and decorated with Danti’s designs between 1580 and 1582. These included a series of enormous frescoes of the four winds, rendered in the style of Titian as voluptuous cupids flanked by images of astronomers at work. Danti also equipped the main room of the tower with an enormous anemometer (wind gauge) attached to a weather vane. He etched into the floor a map of the stars and zodiac, situated so that a small hole in the wall would shine a ray of sunlight onto the map, varying according to the seasonal angle of the sun. This created in the Tower of the Winds a crude seasonal calendar. In 1583, after the reform, Danti was named bishop of Alatri in Italy, where he died in 1586.
The final member of the commission was Antonio Lilius, who represented his late brother’s interest after presenting Aloysius’s ideas in 1576--an event Gregory mentions in his 1582 bull by recalling that ‘a book was brought to us by our beloved son Antonio Lilio, doctor of arts and medicine, which his brother Aloysius had formerly written’.
This ‘book’, still in manuscript form, was easily the most important document in the entire reform process. Yet over the centuries it has disappeared without a trace. What survives is a short booklet issued by the commission, titled
Compendium novae rationis restituendi kalendarium,
‘Compendium of the new rational for reforming the calendar’. This is a synopsis of Lilius’s plan sent out to various experts and important princes, monarchs and prelates for comment.
The
Compendium
was also believed lost until the historian Gordon Moyer located not one but several copies in 1981--all printed in Rome in 1577. The booklet is a short quarto volume containing 24 pages, with a title page that prohibits the selling or reprinting of the book ‘under penalty of excommunication’. All of the copies of the
Compendium
found by Moyer in archives in Florence, Siena and Rome are attached to other short volumes critiquing Lilius’s ideas--with some offering modified plans of their own.
The controversies that continued to swirl around talk of changing the calendar broke down along the familiar lines of science, theology, Church doctrine and the practical impact of reform on the lives of people, governments and the economy. By the 1570s, however, the emphasis was different, with the once potent theological concerns of God and time weighing in far less than debates about astronomic theory, Church cosmology, and how to mechanically come up with the best solution for fixing the calendar.
First on the list of contentious issues was the age-old conundrum: what is the true length of the year?
No one had yet come up with a method for determining the true year beyond a doubt--an issue still not entirely resolved today, given the variability of the earth’s movements--even if the science of astronomy in the sixteenth century was slowly improving. Indeed, by the late 1570s it had become refined enough that Clavius and the commission could seriously consider whether the calendar should be changed to a system based on the actual motions of the earth (or the sun, if you were a follower of Ptolemy), instead of one that used a
mean value
of measurements. The latter was the method employed in both the Julian calendar, with its leap-year system, and by the Church’s lunisolar calendar for determining Easter. Neither calendar had ever been linked to planetary theory; this had long appalled astronomers, who thought that the only way to create an error-free calendar was to drop the idea of a mean and to go on ‘real time’, so to speak.
Clavius, for one, initially hoped to link up the reformed calendar as closely as possible to the true astronomic year. ‘I should think that in order to restore and keep account of astronomy it would be rather important to adopt the true motion,’ he wrote to a friend in Padua on 24 October 1580, ‘but these gentlemen [of the commission] do not understand this for several reasons.’
Lilius, however, argued in favour of a mean, insisting that astronomic theory remained too uncertain despite its advancements. He also believed that trying to devise a calendar based on planetary theory would be far too complicated for people who were not astronomers. What was needed, he said, was a mean calculated to be as close as possible to the true motions of the moon and the perceived motions of the sun.
Apparently the commission agreed, concluding that a calendar must be simple enough for all to understand and use, even if it is slightly off the true astronomic year--the challenge being to make the margin of error as small as possible. Even Clavius evidently came around and was persuaded to go with Lilius, since he later defended this choice after the reform was introduced.
That issue settled, the commission’s next task was to decide which of the many measurements of the year they believed to be most reliable.
Half a century earlier Copernicus had scratched his head and pondered the same question. He had decided that there were 110 good measurements for the tropical year, which seemed to him to speed up and slow down with no discernible pattern. This led him to rely on the more stable sidereal year in
De revolutionibus.
Calendar makers did not have this option, however, since their concern was with creating a ‘year’ that matched the seasons, not the position of the earth in space--the two being slightly different, given that tiresome phenomenon known as the precession of the equinoxes.
To understand this problem, and how it is possible to have two different kinds of years, first visualize the earth as a simple sphere or ball circling the sun. The sidereal year is the amount of time it takes for the earth to circle the sun relative to a fixed celestial object, such as a star; in other words, to reach the exact point in the orbit where it began:
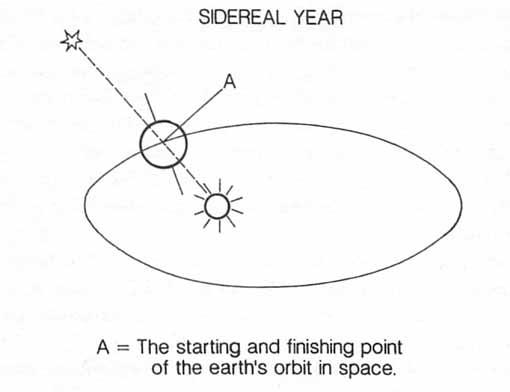
That’s easy. Where it gets tough is when you realize that the earth not only spins around like a top--this is where we get our day and night--but also ‘tilts’, its plane of rotation on its axis tilting relative to the plane of its orbit around the sun (the ecliptic).

To imagine this, think of the globe that sat in the front of your classroom in grammar school, with a line drawn around the fattest part: the equator. Without any tilt, the equator would always be the closest place on the earth to the sun, and we would have no seasons. But in fact the earth does tilt--so that in June the northern hemisphere is aligned with the sun on its ecliptical plane, when it is summer in the north. Roughly six months later the earth tilts so that the southern hemisphere is aligned relative to the plane, making it summer in the south and winter in the north. In between the tilt brings the equator into perfect alignment with the ecliptic, marking the equinoxes that occur in March and September.
Hipparchus in Alexandria was one of the first astronomers to notice the difference between the two types of years when he took measurements of the year according to the equinoxes on his
skaphe,
from 141 to 127 BC. He then must have compared this to the year as measured by the Egyptians, who for centuries had been measuring sidereal year rather than a tropical year. This is because they used as their time ‘ruler’ the annual rise of the Dog Star, Sirius, catching it at the moment it could be seen crossing the peaked point of an obelisk.
Based on Hipparchus’s observations, Claudius Ptolemy three centuries later proposed a simple formula for the precession, hypothesizing that the drift of the tropical year against the stars was fixed, and amounted to one degree per century.
By the time of the calendar commission this had been proven wrong beyond a doubt, first by Arab astronomers and then by others, as the Patriarch Ignatius, the commission’s expert on the Islamic scientific tradition, pointed out to the pope in a letter in 1579 and in his comments on the
Compendium
in 1580. The Arabs, however, had also believed in a fixed rate of precession--coming up with different numbers than Ptolemy--while Copernicus and others had concluded the tropical year was indeed variable, though there was significant disagreement about how much.
This scientific debate over how to calculate a true year was further complicated by the ancient cosmologic theory that most educated people, as well as the Church, still considered true in the sixteenth century. This was that the heavens were composed of a series of concentric spheres, with the earth in the centre and the moon, sun, planets and stars orbiting in successive spheres--a precise and unchanging configuration that could not easily accommodate the possibility of a variable year, or of a starfield that seemed to be drifting slightly each year.
One explanation was that another, even higher sphere of stars might exist, or perhaps several more. This possibility created a great deal of muddle and confusion as traditional astronomers and ecclesiastics struggled mightily to make new and still sketchy data fit into their age-old conception of the universe.
The two astronomers on the calendar panel, Clavius and Danti, each had to convince himself that the year was in fact variable at a time when this was still controversial. For Danti the confirmation came when he took his measurement of the equinoxes in Florence in 1574 and 1575 and found that the length of the year differed from Ptolemy’s measurements. The proof for Clavius came when he constructed a celestial globe for the Collegio Romano and calculated the rate of precession for the years between Copernicus’s observations in 1525 and the year Clavius built his contraption in 1575. This was a change from his earlier blanket acceptance of all things Ptolemaic. Indeed, Clavius kept an open mind about the precession during the commission’s debates, once referring the members to an unpublished essay by a certain Ricciardo Cervini, written in 1550, which argued that there was no precession at all, though Cervini failed to convince anyone.
Given the turmoil over the precession--and the larger controversy looming over Copernicus versus Ptolemy--Aloysius Lilius wisely ignored the entire issue in his solution. According to Clavius--our major source, along with the
Compendium,
for what Lilius was thinking, since Lilius’s own manuscript is lost--the old physician opted simply to choose a value for the year based on what was then one of the more popular astronomical tables. These were the Alfonsine Tables, originally written in 1252 and updated over the years. They gave a mean tropical year of 365 days, 5 hours, 49 minutes and 16 seconds. This was some 30 seconds slower than the true year, but still quite close. The mean value for the year used in the reform itself, which is our calendar year today, is slightly more accurate at 365 days, 5 hours, 49 minutes and 12 seconds--a year that runs only 26 seconds slower than the true year.
This final mean for the Gregorian year allows us to summarize some key measurements, estimates and guesses of the length of the tropical year taken over the centuries, most of which the commission had access to during the decade of their deliberation.