The Code Book (59 page)

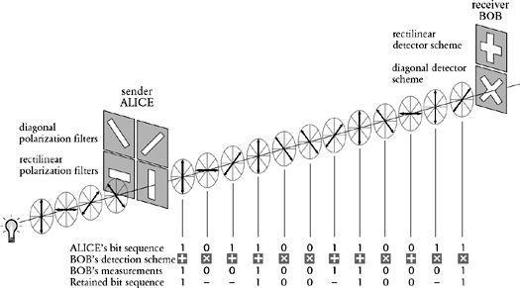
Figure 76
Alice transmits a series of 1’s and 0’s to Bob. Each 1 and each 0 is represented by a polarized photon, according to either the rectilinear (horizontal/vertical) or diagonal polarization scheme. Bob measures each photon using either his rectilinear or his diagonal detector. He chooses the correct detector for the leftmost photon and correctly interprets it as 1. However, he chooses the incorrect detector for the next photon. He happens to interpret it correctly as 0, but this bit is nevertheless later discarded because Bob cannot be sure that he has measured it correctly.
These three stages have allowed Alice and Bob to establish a common series of digits, such as the sequence 11001001 agreed in
Figure 76
. The crucial property of this sequence is that it is random, because it is derived from Alice’s initial sequence, which was itself random. Furthermore, the occasions when Bob uses the correct detector are also random. The agreed sequence does not therefore constitute a message, but it could act as a random key. At last, the actual process of secure encryption can begin.
Table 27
The various possibilities in stage 2 of photon exchange between Alice and Bob.
This agreed random sequence can be used as the key for a onetime pad cipher.
Chapter 3
described how a random series of letters or numbers, the onetime pad, can give rise to an unbreakable cipher-not just practically unbreakable, but absolutely unbreakable. Previously, the only problem with the onetime pad cipher was the difficulty of securely distributing the random series, but Bennett and Brassard’s arrangement overcomes this problem. Alice and Bob have agreed on a onetime pad, and the laws of quantum physics actually forbid Eve from successfully intercepting it. It is now time to put ourselves in Eve’s position, and then we will see why she is unable to intercept the key.
As Alice transmits the polarized photons, Eve attempts to measure them, but she does not know whether to use the +-detector or the ×-detector. On half the occasions she will choose the wrong detector. This is exactly the same position that Bob is in, because he too picks the wrong detector half the time. However, after the transmission Alice tells Bob which scheme he should have used for each photon and they agree to use only the photons which were measured when Bob used the right detector. However, this does not help Eve, because for half these photons she will have measured them using the incorrect detector, and so will have misinterpreted some of the photons that make up the final key.
Another way to think about quantum cryptography is in terms of a pack of cards rather than polarized photons. Every playing card has a value and a suit, such as the jack of hearts or the six of clubs, and usually we can look at a card and see both the value and the suit at the same time. However, imagine that it is only possible to measure either the value or the suit, but not both. Alice picks a card from the pack, and must decide whether to measure the value or the suit. Suppose that she chooses to measure the suit, which is “spades,” which she notes. The card happens to be the four of spades, but Alice knows only that it is a spade. Then she transmits the card down a phone line to Bob. While this is happening, Eve tries to measure the card, but unfortunately she chooses to measure its value, which is “four.” When the card reaches Bob he decides to measure its suit, which is still “spades,” and he notes this down. Afterward, Alice calls Bob and asks him if he measured the suit, which he did, so Alice and Bob now know that they share some common knowledge-they both have “spades” written on their notepads. However, Eve has “four” written on her notepad, which is of no use at all.
Next, Alice picks another card from the pack, say the king of diamonds, but, again, she can measure only one property. This time she chooses to measure its value, which is “king,” and transmits the card down a phone line to Bob. Eve tries to measure the card, and she also chooses to measure its value, “king.” When the card reaches Bob, he decides to measure its suit, which is “diamonds.” Afterward, Alice calls Bob and asks him if he measured the card’s value, and he has to admit that he guessed wrong and measured its suit. Alice and Bob are not bothered because they can ignore this particular card completely, and try again with another card chosen at random from the pack. On this last occasion Eve guessed right, and measured the same as Alice, “king,” but the card was discarded because Bob did not measure it correctly. So Bob does not have to worry about his mistakes, because Alice and he can agree to ignore them, but Eve is stuck with her mistakes. By sending several cards, Alice and Bob can agree on a sequence of suits and values which can then be used as the basis for some kind of key.
Quantum cryptography allows Alice and Bob to agree on a key, and Eve cannot intercept this key without making errors. Furthermore, quantum cryptography has an additional benefit: it provides a way for Alice and Bob to find out if Eve is eavesdropping. Eve’s presence on the line becomes apparent because every time that she measures a photon, she risks altering it, and these alterations become obvious to Alice and Bob.
Imagine that Alice sends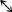 , and Eve measures it with the wrong detector, the +-detector. In effect, the +-detector forces the incoming
, and Eve measures it with the wrong detector, the +-detector. In effect, the +-detector forces the incoming photon to emerge as either a
photon to emerge as either a or a
or a photon, because this is the only way the photon can get through Eve’s detector. If Bob measures the transformed photon with his ×-detector, then he might detect
photon, because this is the only way the photon can get through Eve’s detector. If Bob measures the transformed photon with his ×-detector, then he might detect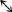 , which is what Alice sent, or he might detect
, which is what Alice sent, or he might detect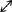 , which would be a mismeasurement. This is a problem for Alice and Bob, because Alice sent a diagonally polarized photon and Bob used the correct detector, yet he might have measured it incorrectly. In short, when Eve chooses the wrong detector, she will “twist” some of the photons, and this will make Bob prone to errors, even when he is using the correct detector. These errors can be found if Alice and Bob perform a brief error-checking procedure.
, which would be a mismeasurement. This is a problem for Alice and Bob, because Alice sent a diagonally polarized photon and Bob used the correct detector, yet he might have measured it incorrectly. In short, when Eve chooses the wrong detector, she will “twist” some of the photons, and this will make Bob prone to errors, even when he is using the correct detector. These errors can be found if Alice and Bob perform a brief error-checking procedure.
The error checking is done after the three preliminary stages, by which time Alice and Bob should have identical sequences of 1’s and 0’s. Imagine that they have established a sequence that is 1,075 binary digits in length. One way for Alice and Bob to check that their respective sequences match would be for Alice to call Bob and read out her complete sequence to him. Unfortunately, if Eve is eavesdropping she would then be able to intercept the entire key. Checking the complete sequence is clearly unwise, and it is also unnecessary. Instead, Alice merely has to pick 75 of the digits at random and check just these. If Bob agrees with the 75 digits, it is highly unlikely that Eve was eavesdropping during the original photon transmission. In fact, the chances of Eve being on the line and not affecting Bob’s measurement of these 75 digits are less than one in a billion. Because these 75 digits have been openly discussed by Alice and Bob, they must be discarded, and their onetime pad is thus reduced from 1,075 to 1,000 binary digits. On the other hand, if Alice and Bob find a discrepancy among the 75 digits, then they will know that Eve has been eavesdropping, and they would have to abandon the entire onetime pad, switch to a new line and start all over again.