The Dancing Wu Li Masters (39 page)
Read The Dancing Wu Li Masters Online
Authors: Gary Zukav

So much for the relationship between the “truth” of a scientific assertion and the nature of reality. There isn’t any. Scientific “truth” has nothing to do with “the way that reality really is.” A scientific theory is “true” if it is self-consistent and correctly correlates experience (predicts events). In short, when a scientist says that a theory is true, he means that it correctly correlates experience and, therefore, it is useful. If we substitute the word “useful” whenever we encounter the word “true,” physics appears in its proper perspective.
Birkhoff and von Neumann created a “proof” that experience violates the rules of classical logic. This proof, of course, is embedded in experience. In particular, it is based upon what does and does not happen with various combinations of polarized light. Finkelstein uses a slightly modified version of Birkhoff and von Neumann’s original proof to demonstrate quantum logic.
The first step of this proof is to experiment with all of the possible combinations of horizontally, vertically, and diagonally polarized light. In other words, the first step is to do what we have done already: discover which light emissions pass through which polarizers. Observe for yourself that light passes through two vertical polarizers, two horizontal polarizers, two diagonal polarizers, a diagonal and a horizontal polarizer, and a diagonal and a vertical polarizer. All of these combinations are called “allowed transitions” because they actually happen. Similarly, observe for yourself that light does not pass through a horizontal and a vertical polarizer, or any other combination of polarizers
oriented at right angles to each other. These combinations are called “forbidden transitions” because they never happen.
The second step of the proof is to make a table of this information called a transition table. A transition table looks like this:
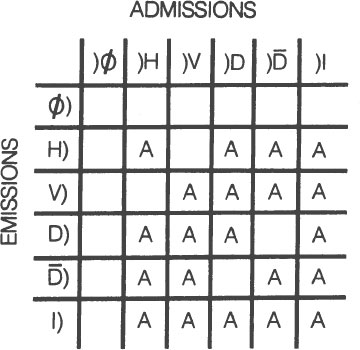
The row of letters on the left are emissions. An emission is just what it sounds like. In this case, an emission is a light wave that is emitted from a light bulb. The “)” sign to the right of a letter indicates an emission. For example, “H)” means horizontally polarized light emitting from a horizontal polarizer. The row of letters on the top are admissions. An admission is the reception of an emission. The “)” sign to the left of a letter indicates an admission. For example, “)H” means a horizontally polarized light wave reaching an eyeball.
The zeros with the lines through them (pronounced “oh”) stand
for the “null process.” The null process means that we decided to go to the movies today and not do the experiment. The null process stands for no emissions, nothing. The letter “I” stands for “identity process.” The identity process is a filter that passes everything. In other words, “I” tells us what kinds of polarized light pass through, say, an open window: namely, every kind.
Two kinds of diagonally polarized light are included in the table to make it complete. The “D” represents light diagonally polarized to the left, and the “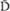 ” represents light diagonally polarized to the right (or the other way round).
” represents light diagonally polarized to the right (or the other way round).
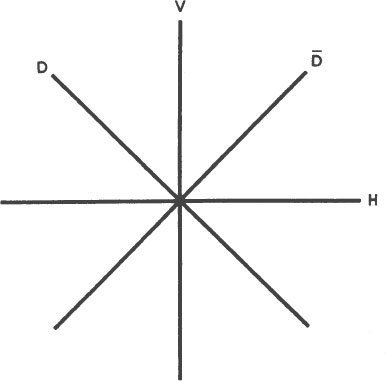
To use the transition table we pick the type of emission in which we are interested and follow it across the table. For example, an emis
sion of horizontally polarized light, H), will pass through another horizontal polarizer, so an “A,” for allowed, is placed in the square where the horizontally polarized emission line intersects the horizontally polarized admission column. Horizontally polarized light also passes through a diagonal polarizer tilted to the left,)D, a diagonal polarizer tilted to the right,)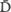 , and an open window, I. An “A” is placed in each appropriate square.
, and an open window, I. An “A” is placed in each appropriate square.
Notice that the square where the horizontally polarized emission line intersects the vertically polarized admission column is blank. This is because horizontally polarized light does not pass through a vertical polarizer. The blank squares show the forbidden transitions. All of the null process squares are blank because nothing happens if we don’t do the experiment. All of the “I” squares are marked “A” because every kind of light, polarized and otherwise, passes through an open window.
The third step in the proof is to make a simple diagram of the information contained in the transition table. The diagram made from this particular transition table looks like this:
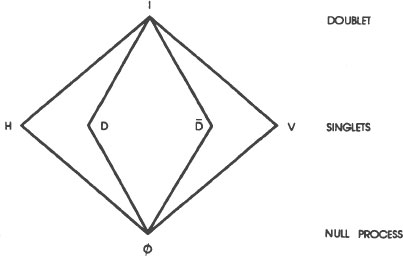
This type of diagram is called a lattice. Mathematicians use lattices to show the ordering of events or elements. Lattices are similar
to the genealogical trees that we construct when we research our family roots. The higher elements include the lower elements. The lines show who is connected to whom and through whom.
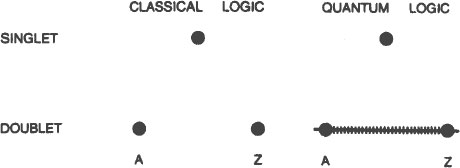
A lattice is not exactly a family tree, but it shows the same kind of inclusive ordering. At the bottom is the null process. Nothing is below the null process since the null process represents no emissions of any kind. In the next level up are the various states of polarization. The elements at this level are called singlets. Singlets are the simplest statements that we can make about the polarization of a light wave. “This light is horizontally polarized,” is the most that we can say about the state of polarization, even though it doesn’t tell us anything else. It is a “maximal but incomplete description,” a limitation inherent in the use of language.
The next level up contains the doublets. In this lattice there is only one doublet. Doublets comprise the next level of maximal but incomplete statements that we can make about the polarization of light in this simple experiment. Lattices representing more complex phenomena can have considerably more levels—triplets, quadruplets, etc. This lattice is the simplest of them all, but it graphically demonstrates the nature of quantum logic.
First, notice that the doublet, I, contains
four
singlets. This is typical of quantum logic but an incomprehensible contradiction to classical logic wherein every doublet, by definition, contains only
two
singlets, no more and no less. Lattices are graphic demonstrations of the quantum postulate that there is always at least one alternative between every “this” and every “that.” In this case, two alternatives (“D” and “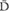 ”) are represented. There are many more available alternatives that are not represented in this lattice. For example, the light in the lattice represented by the symbol
”) are represented. There are many more available alternatives that are not represented in this lattice. For example, the light in the lattice represented by the symbol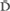 is diagonally polarized at 45°, but we also can polarize light at 46°, 47°, 48½°, etc., and all of these states of polarization could be included in the doublet, I.
is diagonally polarized at 45°, but we also can polarize light at 46°, 47°, 48½°, etc., and all of these states of polarization could be included in the doublet, I.
In both classical logic and quantum logic a singlet can be represented by a dot. In classical logic a doublet is represented by two dots. In quantum logic, however, a doublet is represented by a line drawn
between the two dots.
All of the points on the line
are included in the doublet—not only the two points that define it.