The Essential Galileo (53 page)

Thus you see how much greater is the resistance, arising from contact of the surface of the moving body with the medium, in the case of small bodies than in the case of large. And when one considers that the irregularities on the very small surfaces of fine dust particles are perhaps no smaller than those on the surfaces of larger solids that have been carefully polished, one will see how important it is that the medium should be very fluid and offer no resistance to being thrust aside, easily yielding to a small force. You see, therefore, Simplicio, that I was not mistaken when, not long ago, I said that the surface of a small solid is comparatively greater than that of a large one.
S
IMP.
   I am quite convinced. And believe me, if I were again beginning my studies, I should follow the advice of Plato and start with the mathematical sciences, which proceed very cautiously and admit nothing as established until it has been rigorously demonstrated.
S
AGR.
   This discussion has afforded me great pleasure. But before proceeding further, I should like to hear the explanation â¦
7
[139] S
ALV.
   Let us see whether we cannot derive from the pendulum a satisfactory solution of all these difficulties. And first, as to the question whether one and the same pendulum really performs its oscillations, large, medium, and small, all in exactly the same time, I shall rely upon what I have already heard from our Academician. He has clearly shown that the time of descent is the same along all chords, whatever the arcs that subtend them, whether the arc is 180 degrees (corresponding to the whole diameter), 100 degrees, 60 degrees, 10 degrees, 2 degrees, 1/2 degree, or 4 minutes; it is understood, of course, that these chords all terminate at the lowest point of the circle, where it touches the horizontal plane.
Now, if we consider descent along arcs instead of their chords, then (provided they do not exceed ninety degrees) experiment shows that they are all traversed in equal times; but these times are shorter for the arcs than for the chords, an effect that is all the more remarkable because at first glance one would think just the opposite to be true. For since the terminal points of the two motions are the same and since the straight line included between these two points is the shortest distance between them, it would seem reasonable that motion along this line should be executed in the shortest time; but this is not the case, for the shortest timeâand therefore the most rapid motionâis that employed along the arc of which this straight line is the chord.
As to the times of oscillation of bodies suspended by threads of different lengths, they bear to each other the same proportion as the square roots of the lengths of the thread; or one might say the lengths are to each other as the squares of the times. For example, if one wishes to make the oscillation time of one pendulum twice that of another, one must make its suspension thread four times [140] as long; in like manner, if one pendulum has a thread nine times as long as another, this second pendulum will execute three oscillations during each one of the first. From this it follows that the lengths of the suspending cords bear to each other the [inverse] ratio of the squares of the number of oscillations performed in the same time.
S
AGR.
   Then, if I understand you correctly, I can easily measure the length of a string whose upper end is attached at any height whatever even if this end were invisible and I could see only the lower extremity. For if I attach to the lower end of this string a rather heavy weight and give it a to-and-fro motion, and if I ask a friend to count the number of its oscillations while I, during the same time interval, count the number of oscillations of a pendulum which is exactly one cubit in length, then knowing the number of oscillations which each pendulum makes in the given interval of time one can determine the length of the string. Suppose, for example, that my friend counts 20 oscillations of the long cord during the same time in which I count 240 of my string, which is one cubit in length; taking the squares of the two numbers, 20 and 240, namely, 400 and 57,600, then, I say, the long string contains 57,600 units of length as compared to the 400 contained in my string; and since the length of my string is one cubit, I shall divide 57,600 by 400 and thus obtain 144. Accordingly, I shall call the length of the other string 144 cubits.
S
ALV.
   Nor will you miss it by as much as a palm's breadth, especially if you observe a large number of oscillations.
S
AGR.
   You give me frequent occasion to admire the wealth and profusion of nature when, from such common and even trivial phenomena, you derive facts that are not only striking and new but that are often far removed from what we would have imagined. Thousands of times I have observed, especially in churches, oscillations of lamps suspended by long cords and inadvertently set into motion. But the most I could infer from these observations was the improbability of the view of those who think that such oscillations are maintained by the medium, namely, the air; for, in that case, the air must needs have considerable judgment and little else to do but kill [141] time by pushing back and forth a hanging weight with perfect regularity. But I never dreamed of learning that one and the same body, when suspended from a string a hundred cubits long and pulled aside first through an arc of ninety degrees and then through one degree or half a degree, would employ the same time in passing through the least as through the largest of these arcs; indeed, it still strikes me as almost impossible. Now I am waiting to hear how these same simple phenomena can furnish solutions for those acoustical problemsâsolutions that will be at least partly satisfactory.
S
ALV.
   First of all one must observe that each pendulum has its own time of oscillation so definite and determinate that it is not possible to make it move with any other period than that which nature has given it. For let anyone take in his hand a cord to which a weight is attached and try, as much as he pleases, to increase or diminish the frequency of its oscillations; it will be time wasted. On the other hand, one can confer motion upon even a heavy pendulum that is at rest by simply blowing against it; by repeating these blasts with a frequency which is the same as that of the pendulum, one can impart considerable motion. Suppose that by the first puff we have displaced the pendulum from the vertical by, say, half an inch; then if we add a second puff after the pendulum has returned and is about to begin the second oscillation, we shall impart additional motion; and so on with other blasts provided they are applied at the right instant, and not when the pendulum is coming toward us, since in this case the blast would impede rather than aid the motion. Continuing thus with many impulses, we impart to the pendulum such impetus that a much greater force than that of a single blast will be needed to stop it.
[§10.4 Day II: The Mathematics of
Strength, Size, and Weight]
8
[151] SAGR. While Simplicio and I were awaiting your arrival, we were trying to recall that last consideration which you advanced as a principle and basis for the results you intended to obtain. This consideration dealt with the resistance which all solids offer to fracture, and which depends upon a certain cement that holds the parts glued together so that they yield and separate only under considerable pull. Later we tried to find the explanation for this coherence, seeking it mainly in the vacuum. This was the occasion of our many digressions, which occupied the entire day and led us far afield from the original subject. As I have already stated, that was the investigation of the resistance which solids offer to fracture.
S
ALV.
   I remember it all very well. Resuming the thread of our discussion, whatever the nature of this resistance which solids offer to powerful pulling, there can at least be no doubt of its existence. And although this resistance is very great in the case of a direct pull, it is found, as a rule, to be less in the case of bending forces. Thus, for example, a rod of steel or of glass will sustain a longitudinal pull of a thousand pounds, whereas a weight of fifty pounds would be quite sufficient to break it if the rod were fastened at right angles into a vertical wall. It is this second type of resistance which we must consider, seeking to discover in [152] what proportion it is found in prisms and cylinders of the same material, whether alike or unlike in shape, length, and thickness. In this discussion I shall take for granted the well-known mechanical principle that has been shown to govern the behavior of a lever, namely, that the force bears to the resistance the inverse ratio of the distances that separate the fulcrum from the force and resistance respectively.
S
IMP.
   This was demonstrated first of all by Aristotle, in his
Questions of Mechanics
.
9
S
ALV.
   Yes, I am willing to concede him priority in point of time. But as regards rigor of demonstration, the first place must be given to Archimedes, since upon a single proposition proved in his book
On the Equilibrium of Planes
depends not only the explanation of the lever, but also those of most other mechanical devices.
10
SAGR. Now, since this principle is fundamental to all the demonstrations which you propose to set forth, would it not be advisable to give us a complete and thorough proof of this proposition, unless possibly it would take too much time?
S
ALV.
   Yes, that would be quite proper. But it is better, I think, to approach our subject in a manner somewhat different from that employed by Archimedes. That is, I shall assume merely that equal weights placed in a balance of equal arms will produce equilibriumâ a principle also assumed by Archimedesâand then prove two things: that it is no less true that unequal weights produce equilibrium when the arms of the steelyard have lengths inversely proportional to the weights suspended from them; and that it amounts to the same thing whether one places equal weights at equal distances or unequal weights at distances that bear to each other the inverse ratio of the weights.
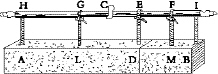
In order to make this matter clear, imagine a prism or solid cylinder,
AB
, suspended at each end to the rod
HI
, and supported by two threads
HA
and
IB;
it is evident that if I attach a thread,
C
, at the middle point of the balance beam
HI
, the entire prism
AB
will, according to the principle assumed, hang in equilibrium since one-half its weight lies on one side, and the other half on the other side, of the point of suspension
C
. Now suppose [153] the prism to be divided into unequal parts by a plane through the line
D
, and let the part
DA
be the larger and
DB
the smaller; this division having been made, imagine a thread
ED
, attached at the point
E
and supporting the parts
AD
and
DB
, in order that these parts may remain in the same position relative to line
HI;
and since the relative position of the prism and the beam
HI
remains unchanged, there can be no doubt but that the prism will maintain its former state of equilibrium. But circumstances would remain the same if that part of the prism which is now held up at the ends by the threads
AH
and
DE
were supported at the middle by a single thread
GL;
and likewise the other part
DB
would not change position if held by a thread
FM
placed at its middle point. Suppose now the threads
HA,ED
, and
IB
to be removed, leaving only the two
GL
and
FM;
then the same equilibrium will be maintained so long as the suspension is at
C.
Now let us consider that we have here two heavy bodies
AD
and
DB
hung at the ends
G
and
F
of a balance beam
GF
in equilibrium about the point
C
, so that the line
CG
is the distance from
C
to the point of suspension of the heavy body
AD
, while
CF
is the distance at which the other heavy body,
DB
, is supported. It remains now only to show that these distances bear to each other the inverse ratio of the weights themselves; that is, the distance
GC
is to the distance
CF
as the prism
DB
is to the prism
DA
âa proposition which we shall prove as follows. Since the line
GE
is half of
EH
, and
EF
is half of
EI
, the whole length
GF
will be half of the entire line
HI
, and therefore equal to
CI;
if now we subtract the common part
CF
, the remainder
GC
will be equal to the remainder
FI
, that is, to
FE;
and if to each of these we add
CE
, we shall have
GE
equal to
CF;
hence
GE
is to
EF
as
FC
is to
CG.
But
GE
and
EF
bear the same ratio to each other as do their doubles
HE
and
EI
, that is, the same ratio as the prism
AD
to
DB
. Therefore, by equidistance of ratios
11
and by inversion, we have that the distance
GC
is to the distance
CF
as the weight
BD
is to the weight
DA.
This is what I desired to prove.