The Lives of Others (34 page)
Read The Lives of Others Online
Authors: Neel Mukherjee

But the dangers of not toeing the line are serious: you fail an exam if you don’t do as you have been told, because you create extra work for a teacher by asking him to think instead of letting him continue on autopilot and, if you fail an exam, it decreases the chances of getting out of the system that will slowly crush you to a flat piece of cardboard.
So Sona does what he has perfected: he becomes two persons, an outer one that goes through the motions required of him, and an inner one that is the true, pure he. The shell does the rote-learning, the core attends to his current obsession with even perfect numbers and how, and if, they relate to the universal set of his greater obsession: primes.
In the almost daily updating of his long list of primes, there were only five Mersenne primes so far (3, 7, 31, 127, 8191), and he had quickly established three obvious things: one, not all 2
n
– 1 numbers were prime; two, not all primes could be expressed as a Mersenne number; three, for 2
n
– 1 to be prime, n should be a prime number. No sooner had he arrived at those generalisations than fissures started appearing in the structure: while the intersecting set of his first and second conclusions needed to be explored further, he found that the third was no guarantee of primality. 2
11
– 1 = 2047 = 23 × 89, to take one such crack running along the edifice. Since he had not found a way of tackling this head-on, he thought that perhaps approaching them from the beautifully contiguous territory of even perfect numbers, numbers whose total factors (including 1, but not the number itself) added up to return the original number, could yield some point of entry.
Faced now with all this unwelcome prying that could very well lead, at least himself, if not his mother and his sister, to the dangerous swamp of emotions, he falls back on his version of thumb-sucking – he teleports his mind to the larger latitudes of numbers, leaving the shell behind.
He says, to no one in particular, ‘I need to do my homework now.’
Of course, he knows Euclid’s proof of the infinity of primes; he kept quiet because that was what he did, what came best to him, but also because he wanted to see how much the mad professor knew, if he really was a professor who knew a few things about mathematics. Who knows what attributes rumour can give people? It’s the volume of Euclid he had held in his hand less than an hour ago that has raked the burning coals of even perfect numbers in him, for who doesn’t know his proof connecting primes and perfect numbers through 2n – 1? If 2n – 1 is a prime, say P, then Euclid’s proof could be rephrased to state that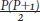 is always an even perfect number.
is always an even perfect number.
Purba looks at the bowed head of her son, rummaging in his tattered school satchel – an old hand-me-down from Suranjan – for his books and pen. The way the loose curls on his head catch the feeble light of the candle makes them look like the cloudy bloom of a drop of ink the moment it hits a bowl of water. It takes her a fraction of a second to work out who he reminds her of.
As far as his intuition leads him, he feels that the converse must be true, that is, if an even number is perfect, then it must conform to the formula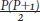 where P is a prime of the form 2
where P is a prime of the form 2
n
–
1. Yet intuition will not do; all this while he has not seen in the eye the centrality of proof to his hunches and feelings. That encounter with Pagla Ashu this evening was one of those moments when chance spoke with pointedness, with almost a design. He will have to prove the hypothesis.
Sona looks exactly like his father. The equivalence Purba has just drawn winds her. Why has it eluded her so far? Whoever said that time blunts all pain did not quite understand that bluntness can wound as grievously as sharp points and edges; Purba finds herself rooted to the spot.
He writes out on a clean sheet of paper: ‘Let N be an even perfect number.
∴
N = 2
n – 1
(2
n
– 1), where 2
n
– 1 is prime.’ The next step is crucial. He stakes everything on it. He has carried it in his head for months now, shuffled it around, waiting for the right pattern to emerge. What if he substituted 2
n
– 1 with an odd number, m? Then N = 2
n – 1
m, and since m is not divisible by 2, it is relatively prime to 2
n – 1
, so that
σ (N) = σ (2
n – 1
m) = σ (2
n – 1
) σ (m) = (2
n
– 1) σ (m) =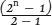 σ (m) = (2
σ (m) = (2
n
– 1) σ (m).
The inspiration with the fourth step, the trick – what a brainwave! – of using 2 – 1 as a denominator comes easily, but he does not know its source. The series of equivalences look like elementary parsing when written down, but each step is an advancement in terms of shape, of design. It is like an explosion in reverse motion, where all the parts come together to cohere into the undiminished whole as if the shattering has never been, yet it is exactly this process of detonation and watching the debris with unblinking attention that yields up the secrets of the architecture of things.
Kalyani asks, ‘What, aren’t you going to give us anything to eat?’
Purba does not hear.
‘You are going to get a haircut this Sunday,’ she says to her son, steadying her voice. ‘You look like a ghost,’ she continues, making her voice stern, almost rebuking, in case he or Kalyani hears any tremulousness in it, ‘with all those curls falling over your forehead and eyes. Like a ghost.’
He barely hears the order. He shifts the forms further:
σ (N) = 2N because N is perfect, so σ (N) = 2N = 2(2
n – 1
m) = 2
n
m. But σ (N) = (2
n
– 1) σ (m) – as above –
∴
2
n
m = (2
n
– 1) σ (m).
He feels that familiar yet rare sensation of his insides going into free fall, that slight loosening of his sphincter, and knows that he will reach the end of the proof successfully.
A few hundred yards away, Ashish Roy comes to a clearing in the impenetrable forest of his mind. A shaft of light pours in. Several questions fly out in a swarming buzz from the undergrowth.
Eeesh, I forgot to ask the boy his name, his address. Now how will I find him?
Navigating the thorny brakes and tangles defeats him at the best of times. The medication he was given after his breakdown was not to cure him, to help him find his way to order and method again, but to keep him quiet, neuter, chained. They are heavy muggers, which silence him with their repeated blows. Who around him wants to see the eked-out, expensive process of becoming better, a path riddled with switchbacks, reversals and doubtful probabilities of success, when one can have the far more convenient option of an end to the thing that bothers everyone around him most – his occasional lapses into shouting fits and violence? Hanging above the pathless and dark forest is the heavy, unlifting pall of haloperidol and quietiapine fumarate. The beast has been muzzled.
But occasionally, very occasionally, there are patches of illumination when he can follow a path from one point to another without being swallowed by the surrounding darkness. It is only a temporary reprieve, given, it seems to him, to taunt him with what he has lost.
But, first, that boy. I must find a way of tracking him down. If I stand where I found him today, exactly at the same time, would that work?
He wants to know which school the boy attends. In the rare gift of intermittent clarity given to him nowadays, something had passed from the boy to him that evening, an electric current, the conduction of some knowledge. He could read what was going on behind the boy’s expression of guarded, private wonder. The boy
knew
. He knew Euclid’s
reductio ad absurdum
proof, he knew Fermat’s two-square theorem. He said that he had got stuck trying to prove it, which meant that he did not know the proof, but – and this causes Ashish Roy’s hobbled mind to exult and soar again –
he was trying to prove it himself.
How many boys of his age – twelve? thirteen? fourteen? – have enough number-theory to even know that theorem, leave alone want to prove it? But, wait, if he doesn’t know it is a theorem, how has he arrived at it? Could he –
here Professor Roy’s hairs stand on end –
could he have worked it out by intuition, or as a by-product to something he is toying with? No school in Calcutta teaches this kind of mathematics. Does he have an exceptional teacher who explores these topics alongside the dead and boring school syllabus? It all comes down to that crucial question: which school does he go to? He looks . . . looks . . . grimy, meagre, except for those large, slow eyes lit up with curiosity and a special kind of intelligence. I have to find him, I have to find him . . . This boy could . . . could . . . could . . .
He has reached the end of the clearing. Beyond it waits the hulking blackness, forever present. It crackles, shifts and leaps on him, obliterating his whole being. He falls down from his bed on to the floor, thrashing and thrashing, as the darkness inside lays its claim on him once more.
VIII
The sound of rain on straw-and-coconut-leaf roofs all night long. And, drowning that, the non-stop croaking of hundreds of frogs, calling out across fields and ponds and the dirt lanes that have all dissolved into runnels of water the colour of milky tea. If you woke up in the middle of the night for some reason, you wouldn’t be able to go back to sleep again because of their varied cacophony. The intervals, rhythms, identification of different types of croaks, perhaps even going so far as to imagine individual frogs each emitting a particular and recurrent line in this mad music – all these sounds and pauses would enter your head and you would be anticipating it, and it would drive you mad.
And it was not just water coming down from the sky. It seemed there was a rain of insects too. I didn’t know the names of half of them. You had your common centipede and millipede and black ants and flying ants that you get in the city, but there were armies of other kinds. When I was small, Mejo-kaka once told me that centipedes could enter your ears while you were sleeping, then they made their way through the ear canal into your brain, where they nested and bred and created a huge colony, which then proceeded to eat up everything inside and then you died, thousands of the creatures leaking out of your nose and ears and eyes. I knew what that typically colourful story by Mejo-kaka was worth now, but it had made a deep impression on me when I was a child. I believed it for a long time and it created a tiny corner of horror mixed with repulsion in my soul. I found that I hadn’t managed to wash it out of myself completely; a mark still remained. Sleeping on the damp floor of Kanu’s hut – I called it a floor, but with rain coming in through the gaps in the thatch it was becoming more mud than floor – the sight of a centipede sent that shudder through me before my rational mind took over.