The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (8 page)
Authors: Sean Carroll

The muon was a complete surprise. We already had the electron; why should it have a heavier cousin? Physicists’ bafflement was captured succinctly in I. I. Rabi’s famous quip, “Who ordered that?” This is exactly the kind of response we’re eventually hoping for from experiments at the LHC—discovering something completely unanticipated, and being sent back to the theoretical drawing board as a result.
It was just the beginning. In 1962, experimentalists Leon Lederman, Melvin Schwartz, and Jack Steinberger showed that there are actually two different kinds of neutrinos. There are electron neutrinos, which interact with electrons and are often created along with them, but also muon neutrinos, which go hand in hand with muons. When the neutron decays, it emits an electron, a proton, and an electron antineutrino; when the muon itself decays, it emits an electron and an electron antineutrino, but also a muon neutrino.
And then the process repeated. In the 1970s, the tau particle was discovered, also negatively charged like the electron but even heavier than the muon. These three particles turn out to be almost identical cousins, differing only in mass. In particular, all of them feel the weak and electromagnetic forces but not the strong interaction. And the tau has its own kind of neutrino, which was long anticipated but not directly detected until the year 2000.
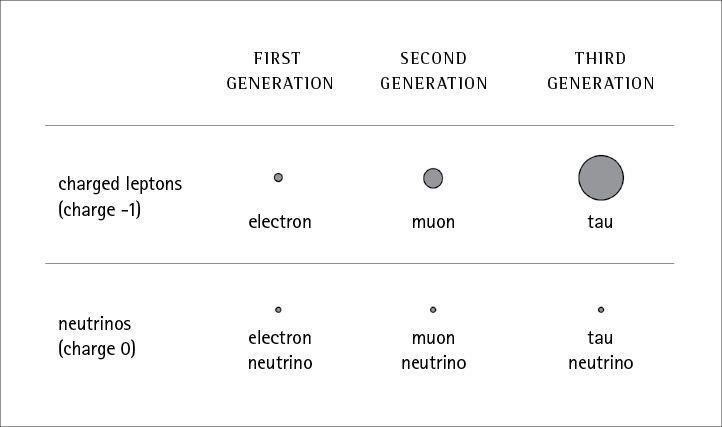
The leptons of the Standard Model, arranged into three generations. Larger circles indicate more massive particles, although the sizes are not to scale.
We’ve worked our way up to no fewer than six leptons, which come in three “families” or “generations”: the electron and its neutrino, the muon and its neutrino, and the tau and its neutrino. It’s perfectly natural to wonder whether there is a fourth generation or beyond lurking out there. Right now the answer is a definite maybe, although there is evidence that three generations are all we get. That’s because the known neutrinos have very small masses—certainly much lighter than the electron. We now know how to search for new light particles, by carefully analyzing the decays of heavier ones. We can count how many neutrino-like particles there must be to account for those decays, and the answer is three. It’s impossible to be sure that there aren’t more lurking out there, perhaps with anomalously large masses, but it may be that we’ve found all the neutrinos (and therefore all the generations of leptons) there are to find.
Quarks and hadrons
Meanwhile the hadrons were not exactly sitting still. The mid-century advent of particle accelerators led to a boom in the number of so-called elementary particles that physicists had discovered. There were pions, kaons, eta mesons, rho mesons, hyperons, and more. Willis Lamb, during his own Nobel lecture in 1955, cracked, “The finder of a new elementary particle used to be rewarded by a Nobel Prize, but such a discovery now ought to be punished by a ten-thousand-dollar fine.”
All of these new particles were hadrons—unlike the leptons, they interacted strongly with neutrons and protons. Increasingly physicists began to suspect that the newcomers weren’t really “elementary” at all, but rather reflected some deeper underlying structure.
The code was finally cracked in 1964 by Murray Gell-Mann and George Zweig, who independently proposed that hadrons were made of smaller particles called “quarks.” Just like leptons, they come in six different flavors: up, down, charm, strange, top, and bottom. The up/charm/top quarks all have electric charge +2/3, while the down/strange/bottom quarks have charge -1/3; these are sometimes grouped as “up-type” and “down-type” quarks, respectively.
Unlike leptons, each flavor of quark really represents a triplet of particles, rather than just one. The three kinds of each quark are fancifully labeled after colors: red, green, or blue. The names are fun, not realistic; you can’t actually see quarks, and if you could they wouldn’t actually have those colors.
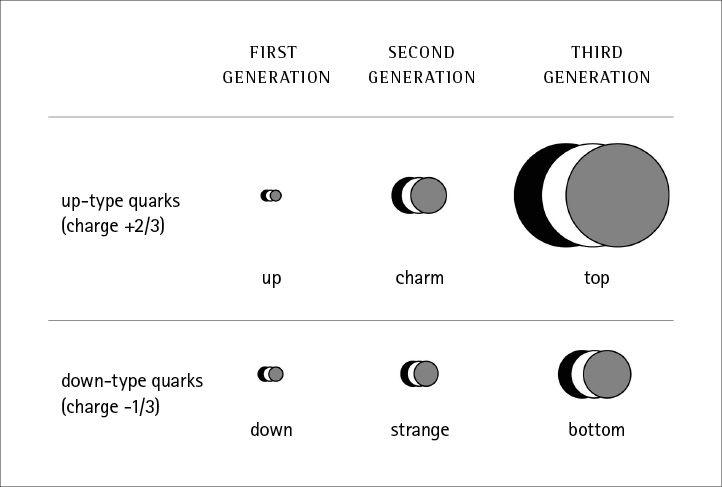
The quarks of the Standard Model, arranged into three generations. Each type of quark comes in three colors. Larger circles indicate more massive particles, although the sizes are not to scale.
Quarks are “confined,” which means that they exist only in combinations inside hadrons, never isolated by themselves. When they combine, it is always into “colorless” combinations. Protons and neutrons each have three quarks inside: A proton is two ups and a down, while a neutron is two downs and an up. One of those quarks will be red, one will be green, and one will be blue; together they make white, which counts as colorless by the terms of this analogy. Later we will see that there are also “virtual” quark-antiquark pairs popping in and out of existence inside the nucleons, but they come in color-anticolor combinations, leaving the overall whiteness unaffected.
It’s impossible to look at the figures portraying the leptons and quarks without noticing some patterns. In both cases we have six types of particles. And these six are precisely arranged into three pairs, with the two particles in each pair differing by one unit of electric charge. Might there be some deeper explanation for this structure? At least in part, the answer is yes. The two particles in each pair, such as an electron and its neutrino, would be identical if it wasn’t for the meddlesome influence of the Higgs field filling empty space. That’s a reflection of the role of the Higgs as a breaker of symmetries, which we’ll examine more carefully later in the book.
The force that doesn’t fit
The fermions of the Standard Model are what give the matter all around us its size and shape. But it’s the forces and their associated boson particles that allow those fermions to interact with one another. Fermions can push or pull on one another by tossing bosons back and forth, or they can lose energy or decay into other fermions by spitting out some kind of boson. Without the bosons, the fermions would simply move along straight lines for all eternity, unaffected by anything else in the universe. And the reason why the universe is so bloody complex and interesting is that these forces are all different, and push and pull in complementary ways.
Physicists often say that there are four forces of nature—they don’t include the Higgs, and not just because it took a long time to discover it. The Higgs is different from the other bosons. The others are what are called “gauge bosons”—as we’ll discuss in Chapter Eight, they are deeply related to underlying symmetries of nature. The graviton is a bit different from the others. Every elementary particle has a certain intrinsic “spin,” and the photon, gluons, and W/Z bosons all have a spin equal to one, while the graviton has a spin of two. (See Appendix One for some details.) We don’t yet know how to reconcile gravity with the demands of quantum mechanics, but it’s still fair to call it a “gauge boson.”
The Higgs, on the other hand, is completely different. It’s what we call a “scalar” boson, which means it has zero spin. Unlike the gauge bosons, the Higgs is not forced on us by a symmetry or any other deep principle of nature. A world without the Higgs would look very different, but it would be perfectly consistent as a physical theory. As important as it is, the Higgs is somewhat of a blemish on the beautiful mathematical structure of the Standard Model. Nevertheless, it is a boson, and therefore it can be exchanged back and forth by other particles, giving rise to a force of nature.

The bosons of the Standard Model. (In this book we include gravitons, although not everyone does.) All the bosons are electrically neutral except for the Ws, and all are massless except for the Ws, Z, and the Higgs.
The Higgs boson is a vibration in the Higgs field, and the Higgs field is what gives mass to all of the massive elementary particles. So the Higgs boson interacts with all of the massive particles in our zoo—the quarks, the charged leptons, and the W and Z bosons. (Neutrino masses aren’t completely understood as yet, so let’s pretend that they don’t interact with the Higgs, although the jury is still out.) And the more massive a particle is, the more strongly it couples to the Higgs. Really it’s the other way around: The more strongly a particle couples to the Higgs, the more mass it picks up by moving through the ambient Higgs field that pervades empty space.
This feature of the Higgs—it interacts more strongly with more massive particles—is absolutely crucial when it comes to studying the beast at the LHC. The Higgs is a heavy particle itself, and even when we produce it we aren’t able to see it directly; it will very rapidly decay into other particles. We expect there will be a certain rate of decay into (for example) W bosons, a different rate of decay into bottom quarks, a different rate of decay into tau mesons, and so forth. And it’s not random—we know exactly how the Higgs is supposed to interact with other particles (because we know how much mass they each have), so we can calculate quite precisely the expected frequency of different kinds of decays.
What we really want is to be wrong. It’s a great triumph to discover the Higgs, but things get really exciting when we are surprised by something new. Searching for invisible particles that are hard to produce and decay quickly into other particles is a challenging task. It’s a matter of patience, precision, and careful statistical analysis. The good news is that the laws of physics (or any one hypothetical version of them) are unforgiving; the predictions for what we should see are unambiguous and inalterable. If the Higgs turns out to be different from what we expect, it will be a clear sign that the Standard Model has finally failed us, and the door to new phenomena has been opened at last.
FOUR
THE ACCELERATOR STORY
In which we trace the colorful history of the unlikely pastime of smashing together particles at ever-higher energies.
W
hen I was about ten years old, I discovered the science section in our local library in Lower Bucks County, Pennsylvania. I was immediately hooked. My favorite books were in astronomy and physics—the 520s and 530s, according to the venerable Dewey Decimal System. One of the books I pored over most intently was a modest volume entitled
High Energy Physics
, by Hal Hellman. I was doing my reading in the late 1970s, but the book had been written in 1968, before the Standard Model was put together—back when quarks were exotic and somewhat scary-sounding theoretical speculations. But hadrons had been discovered in abundance, and
High Energy Physics
was full of evocative photographs of particle tracks, each representing a fleeting glimpse of nature’s secrets.
Many of these photographs had been taken at the mighty Bevatron, one of the leading particle accelerators of the 1950s and ’60s. The Bevatron was located in Berkeley, California, but that’s not where the name came from; it was derived from “billions of electron volts,” the energy the accelerator was able to reach. (As we’ll explain below, an electron volt is a weird unit of energy much beloved by particle physicists.) One billion corresponds to the prefix “giga–,” so a billion electron volts is one GeV, but back in those days Americans would often use “BeV,” and besides, “Gevatron” just doesn’t sound right.