The Particle at the End of the Universe: How the Hunt for the Higgs Boson Leads Us to the Edge of a New World (33 page)
Authors: Sean Carroll

Fermi’s theory provided a good fit to the data, but only if you didn’t push it too hard. Many calculations in quantum field theory proceed by first finding an approximate answer, and then improving that answer bit by bit, essentially by including the contributions from more complicated Feynman diagrams. In the Fermi theory, the original approximation does a very good job, but the next contribution (which is supposed to be a small correction) turns out to be infinitely big. That’s a problem—a big one, which would loom over particle physics throughout the twentieth century. Infinite answers are certainly not right, so they are a sign that your theory is not very good. A theory needs to fit the data, but it also needs to make mathematical sense.
The problem of infinite answers wasn’t confined to the weak interactions; it even plagued electromagnetism, which should be one of the simplest and easiest-to-understand quantum field theories there is. There, however, it turns out that the infinities can be tamed. The process for doing so is known as “renormalization,” and it’s what won the Nobel for Feynman, Schwinger, and Tomonaga.
Some field theories are renormalizable—there are well-defined mathematical techniques for getting finite answers—and some are not. In modern quantum field theory, when a theory fails to be renormalizable, we don’t simply throw it away. We just admit that it’s an approximation at best, perhaps valid only at very low energies, and that some new physics must be present up at high energies to tame the infinities. For a long time, however, nonrenormalizability was taken as a sign that a theory was simply sick. Fermi’s theory of the weak interactions turns out to be nonrenormalizable; it gives infinite answers when we press too hard, and there’s no way to fix them beyond coming up with a better theory.
Julian Schwinger, who had been intrigued by the Yang-Mills idea that more elaborate symmetries could produce connection fields that accounted for nature’s forces, tried to apply the idea to the weak interactions. There is an immediate problem, of course: The Yang-Mills bosons are supposed to be massless, implying a long-range force, while the weak interaction is clearly short-range. Schwinger simply put that problem aside: He started with a Yang-Mills model and made two of the force-carrying bosons massive by hand. This was the first appearance of what we now know as the W
+
and W
-
bosons. (One of the first, anyway. In Leon Lederman’s words: “Later versions of the Fermi theory, most notably by Schwinger, introduced the heavy W
+
and W
-
as weak-force carriers. So did several other theorists. Let’s see: Lee, Yang, Gell-Mann . . . I hate to credit any theorists because 99 percent of them will be upset.”)
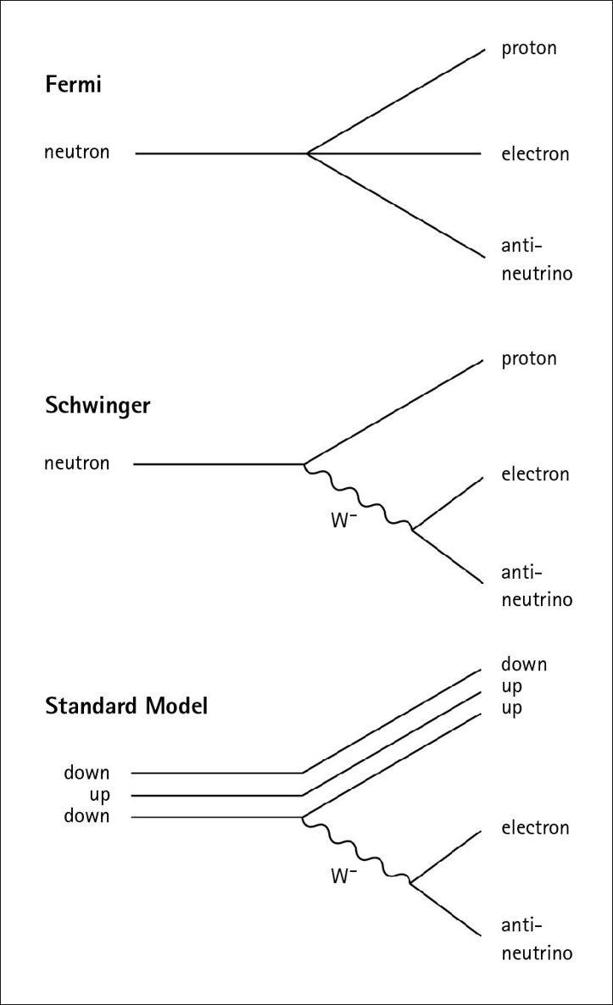
Changing views of the weak interactions, as exemplified by neutron decay. In Fermi’s theory, a neutron decays directly to a proton, an electron, and an antineutrino. Schwinger suggested that a charged W
-
boson was emitted by the neutron, and then decayed into an electron and an antineutrino. He was right, but we now know the neutron is made of three quarks, one of which changes from a down to an up by emitting a W
-
.
The reason why the Yang-Mills bosons were massless in the first place was because of the symmetry on which the theory was based. When Schwinger gave mass to the bosons it implied that this symmetry was broken, but in this case it was an
explicit
breaking, not a
spontaneous
breaking in which the symmetry was hidden by some field that was nonzero in empty space (which hadn’t been invented yet). It wasn’t broken because of a field, it was broken because Schwinger said so. As you might guess, this somewhat ad hoc construction wreaked havoc with the model. For one thing, the renormalizability of electromagnetism depends crucially on the symmetry underlying the theory, and disregarding that symmetry rendered Schwinger’s model nonrenormalizable. Eventually it was realized that a theory of massive gauge bosons would be renormalizable if and only if the masses came from spontaneous symmetry breaking; but that was years down the road.
Nevertheless, Schwinger didn’t persevere with a dodgy theory just because he was stubborn. One property of genius is that you can recognize which kinds of ideas are worth pursuing even though they don’t seem to be working quite yet. A nice property of Schwinger’s model is that it actually predicted three gauge bosons: the two charged W bosons, which were given a mass, and a single neutral gauge boson, which was allowed to remain massless. We all know about a neutral massless gauge boson, of course: It’s the photon. Schwinger was encouraged by the notion that this approach held out the promise of unifying electromagnetism with the weak interactions, which would represent a major step forward in physics. That’s probably what kept him going in the face of the problems with the model.
He didn’t keep going for very long. Schwinger’s paper came out in 1957, and in that same year it was discovered that the weak interactions violate parity. Remember from Chapter Eight (and Appendix One) that particles are either left-handed or right-handed, depending on how they are spinning. Parity violation implied that the weak interactions couple to left-handed particles but not right-handed ones. It’s possible to invent Yang-Mills symmetries that involve only left-handed particles, but we know that electromagnetism
doesn’t
violate parity—it treats left and right on equal footing. This discovery seemed to put the kibosh on Schwinger’s hope of unifying the weak and electromagnetic forces.
Electroweak unification
Sometimes, as a professor, the thing to do is to not give up; it’s to hand off your questions to a graduate student. Happily, Schwinger had a very talented young student available: Sheldon Glashow, who was given the task of thinking about unifying electromagnetism and the weak interactions. Glashow has an expansive and charismatic personality, and as a physicist he enjoys hopping quickly from idea to idea. This propensity served him well in the quest for unification, as he was always very willing to propose one theory and then move on quickly to the next one. After thinking about the question on and off for a few years, he hit on a promising scheme for what would ultimately be called “electroweak unification.”
The sticking point was parity: Electromagnetism preserves it, while the weak interactions violate it. How could they be unified? Glashow’s idea was to introduce two different symmetries: one that treated left-handed and right-handed particles the same, and one that treated them differently. Now, you might think this isn’t a step forward; having two different symmetries doesn’t sound very unified at all. The secret in Glashow’s model was that both symmetries were broken, but in just such a way that a certain combination of the two was left unbroken.
Think of two gear wheels. Either of them can rotate independently; that’s like Glashow’s original two symmetries. But bring them together, the teeth of both wheels meshing with each other. Now they can still move, but they must move together rather than separately. There is less freedom than before. In Glashow’s model, the unbroken symmetry is like the ability to move the wheels together, while the broken symmetry is like the inability to move them at different speeds. The massless, neutral gauge boson corresponding to Glashow’s unbroken symmetry is of course the photon.
This idea seemed to be able to accommodate the known features of both the weak and electromagnetic interactions. (It still suffered from the problem that the gauge boson masses were just put in by hand, and the theory wasn’t renormalizable.) But it deviated from what was known by predicting a new gauge boson: something that was neutral but massive, what we now call the Z. There was no evidence for such a particle at the time, so the model didn’t capture many people’s attention.
While the ingredients Glashow put together in his attempt to unify electromagnetism with the weak interactions might seem a bit arbitrary, there was clearly something sensible about them: Across the ocean in Britain, at Imperial College London, almost exactly the same theory was being put together by Abdus Salam and John Ward. Each physicist individually was very accomplished. Ward, who was born in Britain but spent various years living in Australia and the United States, was a pioneer of quantum electrodynamics. He is probably best known within physics for the “Ward identities” in quantum field theory, mathematical relations that enforce local symmetries. Salam, who was born in Pakistan when it was still joined with India under British control, would eventually become politically active and serve as an advocate for science in the developing world. They were frequent collaborators, and some of their most interesting work was done together, on the question of unifying the forces.
Following very similar logic as Glashow’s, Salam and Ward invented a model with two different symmetries, one of which violated parity and the other which did not, and which predicted a massless photon and three massive weak gauge bosons. Their paper was published in 1964, apparently without being aware of Glashow’s earlier work. Like Glashow, they broke symmetries by hand in their model. Unlike Glashow, they had no excuse for doing so: They were working literally down the hall from Guralnik, Hagen, and Kibble, who were concentrating full-time on spontaneous symmetry breaking.
Part of the failure of communication might have been due to Ward’s naturally reticent nature. In his book
The Infinity Puzzle,
Frank Close relates a revealing story told by Gerald Guralnik:
Guralnik and Ward were having lunch together in a local pub, and Guralnik started to talk about his work—yet to be completed—on hidden symmetry. “I did not get far before [Ward] stopped me. He proceeded to give me a lecture on how I should not be free with my unpublished ideas, because they would be stolen, and often published before I had a chance to finish working on them.” As a result of this admonishment, Guralnik did not ask Ward about the work that he himself was doing with Salam.
Even if one takes such a cautious approach to discussing unpublished work, the most secretive physicist usually isn’t reluctant to talk about
published
results. For whatever reason, however, Salam and Ward didn’t catch on to what Guralnik, Hagen, and Kibble had proposed until several years later. Eventually Salam learned of the work through conversations with Tom Kibble, and for years thereafter would refer to it as the “Higgs-Kibble mechanism.”
Putting it all together
The final pieces of the puzzle were put together in 1967. Steven Weinberg had been high school classmates with Sheldon Glashow at the Bronx High School of Science, but they never directly collaborated on the work in theoretical physics that would lead to them sharing the Nobel Prize with Salam in 1977. Today Weinberg is a respected elder statesman of physics, the author of several influential books as well as frequent essays in
The New York Review of Books
and elsewhere. He also was a major advocate for the Superconducting Super Collider—which he would have been even if the accelerator hadn’t been located in Texas, where he had moved in 1982.
In 1967 Weinberg was a young professor at MIT, driving a red Camaro to campus each day. He was deeply invested in spontaneous symmetry breaking, but he was using it to try to understand the strong interactions. Inspired by a recent paper by Kibble, Weinberg was playing with a set of symmetries that, unbeknownst to him at the time, bore a close resemblance to those considered by Glashow and Salam and Ward before. The problem was that he kept predicting a massless, neutral, gauge boson, which didn’t seem to be there in the strong interactions.
In September of that year, Weinberg suddenly realized that he had been thinking about the wrong problem. His problematic model of the strong interactions worked very well as a theory of the weak and electromagnetic interactions. The annoying massless boson was a feature, not a bug: It was the photon. In a short paper entitled “A Theory of Leptons,” Weinberg put together what every modern graduate student in particle physics would immediately recognize as what’s known as the “electroweak” sector of the Standard Model. In the references he cited Glashow’s paper, but he still wasn’t aware of the one by Salam and Ward. Using Kibble’s ideas, he was able to make a direct prediction for the masses of the W and Z bosons—something Glashow and Salam and Ward weren’t able to do, as they had inserted the masses by hand. Weinberg accounted for the mechanism by which all the fermions in the theory acquired mass, as well as the gauge bosons. He even noted that the model might possibly be renormalizable, although he wasn’t able to offer any convincing arguments at the time. A coherent theory of electroweak unification had finally been assembled.
At almost precisely the same time, Kibble and Salam finally realized their mutual interest in symmetry breaking, and Kibble explained the theory to Salam. Salam figured out that he could rework the unified model he had proposed with Ward to include symmetry-breaking scalar bosons, and gave lectures on his ideas to a small audience at Imperial. For unknown reasons, Salam didn’t write up these ideas right away; he was extremely prolific as a physicist, but his major focus in those days was on gravity, not on subatomic forces. Consequently, his proposal to add a Higgs mechanism to the Salam-Ward model didn’t appear in print until a year later, when he included it in the proceedings from a conference talk (where he also cites Weinberg’s paper).