Think: A Compelling Introduction to Philosophy (30 page)

Experience stretches no further than limited portions of space and
time. In particular, all our experience belongs to the past and present. If we make inferences to the future, then these are inferences,
and Hume wants to know the'chain of reasoning' that they employ.

The inference from what is true of one limited region of space
and time to a conclusion true of different parts of space and time is
called inductive inference. What Hume is bothered about has become known as the problem of induction.

THE LOTTERY FOR THE
GOLDEN HARP

Here is a science fiction. You are disembodied spirits, inhabiting a
kind of Heaven. I am God. I tell you that I am about to embody you, to give you lives to lead in a physical universe that I have prepared
for you: Earth. At the end of your period in this universe, you will
return to Heaven. Unlike normal human life, you will all live the
same period: nine acts, let us say.

To make things interesting, I am going to offer you a kind of lottery. Each of you will get a ticket. The tickets correspond to the
colour of the clear midday sky for each of the nine acts. I covenant
with you, as gods do, that I won't change the colour at any time
other than the beginning of an act. Just one of you is going to have
a ticket that corresponds to the actual colour of the sky in every act.
I also tell you that this person, the winner, will get the Golden Harp
when you cone hack to Heaven. This is a very valuable prize.
Heaven is good, but Heaven with the Golden Harp is even better.
So a ticket might look like this:

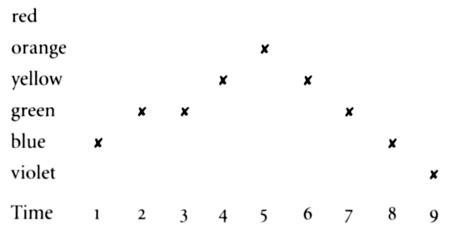
This ticket corresponds to the sky starting blue, going green, then
yellow and orange, before darkening hack to blue and even violet.
Call the person with this ticket, Wavy.

Sonic of you (six of you) get straight tickets:

Call this ticket, Straightie.

If there is going to be just one ticket for each of you, there need
to be 69of you, which is a very large number indeed, to have a ticket
corresponding to each possible distribution of the colours. And
correspondingly, your chance of being the winner is only 1/6y,
which is a very small number.

Hume insists that we cannot know anything right from the beginning in this situation. We cannot have a priori knowledge which
ticket will win. Antecedently, while we are still excitedly discussing
tickets, there is no reason to prefer one to another. For all we know
God may favour waves, or straight lines. Or he may favour Kinkie:

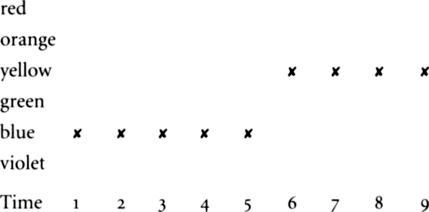
The clear midday sky starts off blue for the first five acts, and then
turns yellow, and stays like that for the rest. So in heaven, before we
get any experience of the world God is about to put us into, no
ticket has any better chance than any other.

Well, now we go to Earth.

Immediately, 5/6 of us can throw our tickets away. Any ticket not
showing blue in the first square is a loser. And similarly, on the first
day of each subsequent act, 5/6 of the survivors can throw their
tickets away, until at the beginning of the ninth act, only six remain. And a day after that, there is a single winner.

Now let us draw the curtain hack towards the end of the fifth act.
Each of Straightie and Kinkie has been doing well. They have seen
their competitors fall away, on five previous occasions. In fact, the
number ofsurvivors in the lottery has dropped from 6'down to 6',
and their chances of being the winner have risen accordingly.

But suppose they get into an argument with each other. Suppose
Straightie urges Kinkie that his ticket is far the more likely winner,
so that he will swap it with Kinkie but only for a terrific price. We
would probably side with Straightie. But suppose that Kinkie resists, urging that there is no reason in what has happened so far to
bet on Straightie rather than on him. What can they say to each
other?

Each can point to their track record of success. But it is the same
track record for each of them. They each have their five hits. And
there is nothing else to go on. After all, neither of them can peer
into the future. Like us, they are stuck in time, and cannot peek out
of it.

What Straightie would like is an argument in favour of the In1i- fortuity of nature. In other words, an argument saying that since
God has started off with a blue sky, and stuck with it so far, probably he is going to go on sticking with it. But Kinkie can point out
that God has started off with an as-per-Kinkie sky, and by equal
reasoning urge that he is probably going to stick with that.

Straightie wants the argument that Hume says he cannot find.
But, as I said, in our bones we all side with Straightie. What's wrong
with arguing that since nature has been uniform so far, it will probably go on being uniform?

It is impossible, therefore, that any arguments from experience can prove this resemblance of the past to the future; since
all these arguments are founded on the supposition of that resemblance.

Of course, Hume knows that we all learn from experience, and that
we all rely upon the uniformity of nature. He thinks we share this
natural propensity with animals. It is just that this is all it is: an exercise of nature. It is a custom or habit, but it has no special claim
in reason. When we reason inductively there is a way in which our
premises can be true and our conclusion false. Nature can change.
In fact, there are many ways, since nature can change in many ways.
There is no contradiction in imagining this. And now, it seems, we
cannot even argue that such changes are improbable. We only think
that because they have not occurred within our experience. But
taking our experience to be representative, in this regard as in any
other, presupposes the uniformity of nature. It seems that we engineer a bridge between past and future, but cannot argue that the
bridge is reliable.

CHANCY STUFF

Here is a problem quite a long way from the problem of induction,
but that introduces an incredibly useful tool for thinking about
many things. It is a problem most people get wrong.

Suppose you decide to check yourself out for some disease. Suppose that this disease is quite rare in the population: only about one
in a thousand people suffer from it. But you go to your doctor, who
says he has a good test for it. The test is in fact over 99 per cent reliable! Faced with this, you take the test. Then-horrors!-you test
positive. You have tested positive, and the test is better than 99 per
cent reliable. How bad is your situation, or in other words, what is
the chance you have the disease?

Most people say, it's terrible: you are virtually certain to have the
disease.

But suppose, being a thinker, you ask the doctor a bit more
about this 99 per cent reliability. Suppose you get this information:

(i) If you have the disease, the test will say you have it.

(2) The test sometimes, but very rarely, gives `false positives'. In only a very few cases-around I per cent-does it
say that someone has the disease when they do not.

These two together make up the better than 99 per cent reliability.
You might think that you are still virtually certain to have the disease. But in fact this is entirely wrong. Given the facts, your chance
of having the disease is a little less than io per cent.

Why? Well, suppose i,ooo people take the test. Given the general
incidence of the disease (the `base rate'), one of them might be expected to have it. The test will say he has it. It will also say that t
per cent of the rest of those tested, i.e. roughly ten people, have it.
So eleven people might be expected to test positive, of whom only
one will have the disease. It is true the news was bad-you have
gone from a i in i,ooo chance of disease to a i in it chance-hut it is
still far more probable that you are healthy than not. Getting this
answer wrong is called the fallacy of ignoring the base rate.

How should we think accurately about chances in a circumstance like this?

We should start with a formula for the probability of one thing
given another. Suppose we ask what the probability is of (a) some
random person in a class wearing Levi jeans. Perhaps 20 per cent.
And what is the probability of (b) some random person wearing a
Levi jacket? Perhaps 20 per cent also. So what is the probability of a
random person both wearing the jeans, and the jacket? You might
think 20/100 X 20/100 = 4 per cent. But that would be wrong. For
the two events are not necessarily independent. That means, the
chance of someone wearing the jacket is very likely different if they
are wearing the jeans. Perhaps nearly everyone who wears those
jeans wears those jackets and vice versa. In that case the probability
of (a) and (b) both being true of a random person would itself be
20 per cent. Or perhaps the fashion gurus say that you must never
wear both. In that case the chance of (a) and (b) both being true
might be zero.

To get this right we need an expression for the probability of
someone wearing the jacket given that he is wearing the jeans. The
probability of (a) given (b) is written Prob (a/b). The probability of
(b) given (a) is Prob (b/a). Then the right figure is this: