Warped Passages (50 page)

The equivalence between ten-dimensional superstring theory and eleven-dimensional supergravity vindicated Paul Townsend at Cambridge and Michael Duff, then at Texas A&M. For a long time, string theorists had largely rebuffed and maligned their work on eleven-dimensional supergravity—they couldn’t understand why Duff and Townsend were wasting their time with this theory when string theory was so obviously the physics of the future. After Witten’s talk, string theorists had to concede that eleven-dimensional supergravity was not only interesting, it was equivalent to string theory!

I realized how much attention this surprising result about duality was receiving when I was on a plane returning from London. A fellow passenger, who turned out to be a rock musician, saw that I was reading some physics papers. He came over and asked me whether the universe had ten or eleven dimensions. I was a little surprised. But I did answer and explained that in some sense, it is both. Since the ten-and eleven-dimensional theories are equivalent, either one can be considered correct. The convention is to give the number of dimensions in whichever of the theories has weakly interacting strings and thus a lower physical value of the string coupling.

But unlike the couplings associated with Standard Model forces, whose strength we can measure, we don’t yet know the size of the string coupling. It might be weak, in which case perturbation theory
can be applied directly; or it might be strong, in which case you would be better off using perturbation theory in the dual description. Without knowing the value of the string coupling, we have no way of knowing which, if either, of the two descriptions is the simpler way to describe string theory as it applies to the world.
^*

And there were more duality surprises at Strings ’95. Until then, most string theorists had thought there were five versions of superstring theory, each of which included different forces and interactions. At Strings ’95, Witten (and before that, Townsend and another British physicist, Chris Hull) demonstrated dualities between pairs of versions of superstring theory. And over the course of 1995 and 1996, string theorists showed that all these versions of ten-dimensional theories were dual to one another, and, furthermore, were dual to eleven-dimensional supergravity. Witten’s talk had triggered a veritable duality revolution. With the extra input from the nature of branes, the five apparently distinct superstring theories were shown to be the same theory in different guises.

Because the various versions of string theory are actually the same, Witten concluded that there must exist a single theory that encompasses eleven-dimensional supergravity and the different manifestations of string theory, whether or not they contain only weak interactions. He named the new eleven-dimensional theory M-theory—the theory I mentioned at the beginning of this chapter. You can get any known version of superstring theory from M-theory. But M-theory also extends beyond the known versions to domains we have yet to understand. M-theory has the potential to give a more unified, coherent picture of the superstring and to fully realize string theory’s potential as a theory of quantum gravity. However, more pieces or patterns are needed before string theorists understand M-theory sufficiently well to pursue these goals. If the known versions of superstring theory are shards taken from an archeological dig, M-theory is the sought-after enigmatic artifact that would piece them
all together. No one yet knows the best way to formulate M-theory. But string theorists now think of it as their primary goal.

More On Duality

This section gives a little more detail about the particular duality I mentioned above, the one between ten-dimensional superstring theory and eleven-dimensional supergravity. I won’t use these explanations later, so feel free to skip ahead to the next chapter if you like. But since this is a book about dimensions, a digression about the duality between two theories with different dimensions doesn’t seem entirely out of place.

One feature that makes duality a little more reasonable is that one of the two theories always contains strongly interacting objects. If the interactions are strong, only rarely can you directly deduce the physical implications of the theory. Although it’s strange to think of a theory that looks ten-dimensional being best described by another, totally different, eleven-dimensional theory, it seems less strange when you remind yourself that your ten-dimensional theory contained such strongly interacting objects that you couldn’t predict what was happening there in the first place. All bets were off anyway.

There are nonetheless many baffling features about a duality between theories with different numbers of dimensions. And in the particular case of the duality between ten-dimensional superstring theory and eleven-dimensional supergravity, at first glance there appears to be an extremely basic problem. Ten-dimensional superstring theory contains strings, whereas eleven-dimensional supergravity does not.

Physicists used branes to solve this puzzle. Even though eleven-dimensional supergravity does not contain strings, it does contain 2-branes. But unlike strings, which have only one spatial dimension, 2-branes have two (as you might have guessed). Now, suppose that one of the eleven dimensions is rolled up into an extremely tiny circle. In that case, a 2-brane that encircles the rolled-up circular dimension looks just like a string. The rolled-up brane appears to have only one spatial dimension, as illustrated in Figure 69. This means that
eleven-dimensional supergravity theory with a rolled-up dimension appears to contain strings, even though the original eleven-dimensional theory does not.

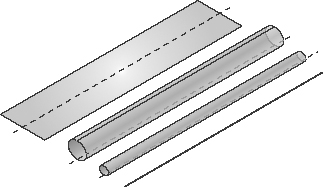
Figure 69.
A brane with two spatial dimensions that is rolled up on a very small circle looks like a string.

This might sound like a cheat, since we have already argued that a theory with a curled-up dimension always appears to have fewer dimensions at long distances and low energies, so you wouldn’t be surprised to find that an eleven-dimensional theory with a rolled-up dimension acts like a ten-dimensional theory. If you want to show that these ten-and eleven-dimensional theories are equivalent, why should it be sufficient to study the eleven-dimensional theory when one of the dimensions is rolled up?

The key to the answer is that in Chapter 2 we only showed that a rolled-up dimension is invisible at long distances or low energies. Edward Witten went further at Strings ’95. He demonstrated the equivalence of the ten-and eleven-dimensional theories by showing that the eleven-dimensional supergravity theory with one of the dimensions curled up is completely equivalent to ten-dimensional superstring theory, even at short distances. When a dimension is curled up, you can still distinguish points at different locations along this dimension if you look closely enough. Witten showed that everything about the dual theories is equivalent, even those particles which have enough energy to probe distances smaller than the curled-up dimension’s size.

Everything about the eleven-dimensional supergravity theory with a curled-up dimension—even short distances and high-energy processes and objects—has a counterpart in the ten-dimensional superstring theory. Furthermore, the duality holds true for a dimension curled up in a circle of any size, no matter how large. Earlier, when we looked at a rolled-up dimension, we argued only that a small curled-up dimension would not be noticed.

But how can theories with different numbers of dimensions possibly be the same? After all, the number of dimensions of space is the number of coordinates that we need to specify the position of a point. The duality could be true only if superstring theory always uses an additional number to describe pointlike objects.

The key to the duality is that in superstring theory, there are special new particles that you can uniquely identify only by specifying the value of the momentum in nine spatial dimensions and also the value of a charge, whereas in eleven-dimensional supergravity you need to know momentum in ten spatial dimensions. Notice that even though you have nine dimensions in one case and ten in the other, in both cases you would need to specify ten numbers: nine values of momentum and a charge in one case, and ten values of momentum in the other.

Ordinary uncharged strings don’t pair with objects in the eleven-dimensional theory. Because you need to know eleven numbers to locate an object in the spacetime of the eleven-dimensional theory, only particles that carry charge have eleven-dimensional mates. And the partners of the objects in the eleven-dimensional theory particles turn out to be branes—namely, charged, pointlike branes called D
₀
-branes. String theory and eleven-dimensional supergravity are dual because for every D
₀
-brane of a given charge in ten-dimensional superstring theory,
^*
there is a corresponding particle with a particular eleven-dimensional momentum. And vice versa. The objects of the ten-and eleven-dimensional theories (and their interactions as well) are exactly matched.

Although charge might seem very different from momentum in a particular direction, if every object with a particular momentum in the eleven-dimensional theory matches onto an object with a
particular charge in the ten-dimensional one (and vice versa), it is up to you whether you want to call that number momentum or charge. The number of dimensions is the number of independent directions of momentum—that is, the number of different directions in which an object can travel. But if momentum along one of the dimensions can be replaced by a charge, the number of dimensions isn’t really well defined. The best choice is determined by the value of the string coupling.

This astonishing duality was one of the first analyses in which branes proved instrumental. Branes were the additional ingredients that were needed for different string theories to match onto each other. But the critical feature of string theory branes that is important for their application in physical theories is that they can house particles and forces. The next chapter explains why.

What to Remember

• String theory is a misnomer: string theory also contains higher-dimensional branes.
  D-branes
  are a type of brane in string theory on which open strings (strings that don’t loop back on themselves) must end.
  
• Branes played a role in many of the important string theory developments of the last decade.
  
• Branes were critical in demonstrating
  duality
  , which showed that superficially different versions of string theory are in fact equivalent.
  
• At low energies, ten-dimensional superstring theory is dual to eleven-dimensional
  supergravity
  —an eleven-dimensional theory that contains supersymmetry and gravity. Particles in one theory match onto branes in the other.
  
• The results about branes from this chapter will not be relevant later on. These results do, however, explain some of the excitement about branes in the string theory community.
  

16

Bustling Passages: Braneworlds

Welcome to where time stands still.

No one leaves and no one will.

Metallica

Icarus III was becoming increasingly disillusioned with Heaven. He had expected it to be a liberal, forgiving environment. But instead, gambling was prohibited, metal silverware was forbidden, and smoking was no longer allowed. The most restrictive constraint of all was that Heaven was stuck on a Heavenbrane; its residents were forbidden to travel into the fifth dimension.

Everyone on the Heavenbrane knew about the fifth dimension and the existence of other branes. In fact, the righteous Heavenbraners often whispered about the unsavory characters sequestered on a Jailbrane not too far away. However, the Jailbraners couldn’t hear any of the slander that Heavenbraners spread about them, so all remained peaceful in the bulk and on the branes.

From the perspective of the “duality revolution,” you might think that branes were a great boon to people trying to connect string theory to the visible universe. If all of the different formulations of string theory are in fact one and the same, physicists would no longer be faced with the daunting task of finding the rules by which nature chooses among them. There is no need to play favorites if all of the string theories appearing in different guises are actually the same.

But nice as it would be to think that we are closer to finding the connection between string theory and the Standard Model, the task is not so simple. Although branes were critical to the dualities that reduced the number of distinct manifestations of string theory, they actually increased the number of ways in which the Standard Model might emerge. That is because branes can house particles and forces that string theorists didn’t take into account when they originally developed string theory. Because of the many possibilities as to what types of brane exist and where they are situated in the higher-dimensional space of string theory, there are conceivably many new ways to realize the Standard Model in string theory that no one had thought about before. The forces of the Standard Model do not necessarily arise from a single fundamental string: they could instead be new forces that emerge from strings extended among different branes. Although dualities tell us that the original five versions of superstring theory are equivalent, the number of braneworlds that are conceivable in string theory is stupendous.