Why Beauty is Truth (8 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

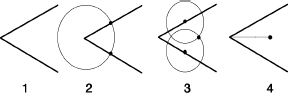
How to bisect an angle with straightedge and compass.
Given (1) an angle between two line segments, (2) place your compass tip where the segments meet, and draw a circle, which crosses the segments at two points, one on each (dark blobs). Now (3) draw two circles of equal radius, one centered at each of the new points. They meet in two points (only one is marked), and (4) the required bisector (dotted) runs through both of these.
By repeating this construction, you can divide an angle into four equal pieces, or eight, or sixteenâthe number doubles at each step, so we obtain the powers of 2, which are 2, 4, 8, 16, 32, 64, and so on.
As I mentioned, the main aspect of
The Elements
that affects our story is not what it contains but what it doesn't. Euclid did not provide any method for:
â¢Â Dividing an angle into
three
exactly equal parts (“trisecting the angle”).
â¢Â Constructing a regular 7-sided polygon.
â¢Â Constructing a line whose length is equal to the circumference of a given circle (“rectifying the circle”).
â¢Â Constructing a square whose area is equal to that of a given circle (“squaring the circle”).
â¢Â Constructing a cube whose volume is exactly twice that of a given cube (“duplicating the cube”).
It is sometimes said that the Greeks themselves saw these omissions as flaws in Euclid's monumental work and devoted a great deal of effort to
repairing them. Historians of mathematics have found very little evidence to back up these claims. In fact, the Greeks could solve all of the above problems, but they had to use methods that were not available within the Euclidean framework. All of Euclid's constructions were done with an unmarked straightedge and compass. Greek geometers could trisect angles using special curves called conic sections; they could square the circle using another special curve called a quadratrix. On the other hand, they do not seem to have realized that if you can trisect angles, you can construct a regular 7-gon. (I
do mean
7-gon. There is an easy construction for a 9-gon, but there is also a very clever one for a 7-gon.) In fact, they apparently did not follow up the consequences of trisection at all. Their hearts seem not to have been in it.
Later mathematicians viewed Euclid's omissions in a rather different light. Instead of seeking new tools to solve these problems, they began to wonder what could be achieved with the limited tools Euclid used: straightedge and compass. (And no cheating with marks on the ruler: the Greeks knew that “neusis constructions” with sliding rulers and alignment of marks could trisect the angle effectively and accurately. One such method was devised by Archimedes.) Finding out what could or could not be done, and proving it, took a long time. By the late 1800s we finally knew that none of the above problems can be solved using straightedge and compass alone.
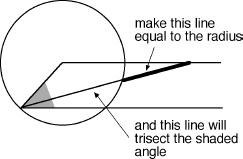
How Archimedes trisected an angle.
This was a remarkable development. Instead of proving that a particular method solved a particular problem, mathematicians were learning to prove the opposite, in a very strong form:
no
method of this-and-that kind is capable of solving such-and-such problem. Mathematicians began
to learn the inherent limitations of their subject. With the fascinating twist that even as they were stating these limitations, they could prove that they genuinely
were
limitations.
In the hope of avoiding misconceptions, I want to point out some important aspects of the trisection question.
What is required is an
exact
construction. This is a very strict condition within the idealized Greek formulation of geometry, where lines are infinitely thin and points have zero size. It requires cutting the angle into three
exactly
equal parts. Not just the same to ten decimal places, or a hundred or a billionâthe construction must be
infinitely
precise. In the same spirit, however, we are allowed to place the compass point with infinite precision on any point that is given to us or is later constructed; we can set the radius of the compass, with infinite precision, to equal the distance between any two such points; and we can draw a straight line that passes
exactly
through any two such points.
This is not what happens in messy reality. So is Euclid's geometry useless in the real world? No. For instance, if you do what Euclid prescribes in Proposition 9, with a real compass on real paper, you get a pretty good bisector. In the days before computer graphics, this is how draftsmen bisected angles in technical drawings. Idealization is not a flaw: it is the main reason mathematics works at all. Within the idealized model, it is possible to reason logically, because we know exactly what properties our objects have. The messy real world isn't like that.
But idealizations also have limitations that sometimes make the model inappropriate. Infinitely thin lines do not, for example, work well as painted lane markers on roads. The model has to be tailored to an appropriate context. Euclid's model was tailored to help us work out the logical dependencies among geometrical statements. As a bonus, it may also help us understand the real world, but that certainly wasn't central to Euclid's thinking.
The next comment is related, but it points in a rather different direction. There is no problem finding constructions for trisecting angles approximately. If you want to be accurate to one percent or one thousandth of a percent, it can be done. When the error is one thousandth of the thickness of your pencil line, it really doesn't matter for technical drawing.
The mathematical problem is about
ideal
trisections. Can an arbitrary angle be trisected
exactly?
And the answer is “no.”
It is often said that “you can't prove a negative.” Mathematicians know this to be rubbish. Moreover, negatives have their own fascination, especially when new methods are needed to prove them. Those methods are often more powerful, and more interesting, than a positive solution. When someone invents a powerful new method to characterize those things that can be constructed using straightedge and compass, and distinguish them from those that cannot, then you have an
entirely new way of thinking.
And with that come new thoughts, new problems, new solutionsâand new mathematical theories and tools.
No one can use a tool that hasn't been built. You can't call a friend on your cell phone if cell phones don't exist. You can't eat a spinach soufflé if no one has invented agriculture or discovered fire. So tool-building can be at least as important as problem-solving.
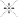
The ability to divide angles into equal parts is closely related to something much prettier: constructing regular polygons.
A polygon (Greek for “many angles”) is a closed shape formed from straight lines. Triangles, squares, rectangles, diamonds like this â, all are polygons. A circle is not a polygon, because its “side” is a curve, not a series of straight lines. A polygon is regular if all of its sides have the same length and if each pair of consecutive sides meet at the same angle. Here are regular polygons with 3, 4, 5, 6, 7, and 8 sides:

Regular polygons.
Their technical names are equilateral triangle, square, (regular) pentagon, hexagon, heptagon, and octagon. Less elegantly, they are referred to as the regular 3-gon, 4-gon, 5-gon, 6-gon, 7-gon, and 8-gon. This terminology may seem ugly, but when it becomes necessary to refer to the regular 17-sided polygonâas it shortly willâthen the term “17-gon” is far
more practical than “heptadecagon” or “heptakaidecagon.” As for the 65,537-gon (yes, that too!)âwell, you get the picture.
Euclid and his predecessors must have thought a great deal about which regular polygons can be constructed, because he offers constructions for many of them. This turned out to be a fascinating, and decidedly tricky, question. The Greeks knew how to construct regular polygons when the number of sides is