X and the City: Modeling Aspects of Urban Life (13 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam


As I write this, my daughter and son-in-law have sold their house and moved into a somewhat larger one. Could it be that the bamboo drove them out?
Grass also has a propensity to grow, but it seems that my lawn is never as green and lush as everyone else’s. Despite my secret desire to cover it with Astroturf, or green-painted concrete, I bought yet another bag of grass seed awhile ago. It can be thought of as a rectangular box with dimensions approximately 2 × 1.5 × 0.5 ft
3
. So let’s think about the quantity of seed in this bag . . .
=
N
: PROBLEM
Estimate (i) the number of seeds in such a bag (assumed full), and (ii) how many such bags would be required to seed, say, a golf course with area one square mile.
(i) We need first to estimate the volume of a typical grass seed. Since I started this question using the more familiar British units (for those in the U.S. at least), as opposed to the easier metric units, I’ll continue in this vein. Examining a seed, I estimate a typical seed to be a rectangular box with approximate dimensions 1/5 in × 1/20 in × 1/20 in, or about 1/2000 cu in. The bag’s volume is about 25 × 20 × 5 = 2500 cu in. Therefore the number of seeds is
N
= 2500 ÷ (1/2000) = 5 × 10
6
, or 5 million! How many seeds would there be to seed one square mile?
(ii) Let’s assume that the grass is seeded uniformly with about 10 to 20 seeds per sq in. (you can change this seed density to suit your own estimates). I’ll go with the lower figure. Since a (linear) mile contains 5280 × 12 ≈ 6 × 10
4
inches, a square mile contains the square of this number, and with 10 seeds/sq in we have the quantity of seeds as approximately 10 × (6 × 10
4
)
2
≈ 4 × 10
10
(that’s 40 billion!). Finally, dividing this figure by the average number of seeds per bag we obtain 4 × 10
10
÷ 5 × 10
6
, or about 10,000 bags. I could round this up because the first figure is unlikely to be correct (e.g., it could be 6 or 9, and still be within the order of accuracy we anticipate). I wonder what the local golf club would say.
At the university where I am employed, there is a lovely collection of orchids, some of them very rare. Suppose that a botanist (let’s call him Felix) wishes to grow one of these rarer varieties in the greenhouse. From his previous attempts, he has concluded that the probability that a given bulb will mature is about one third. He decides to plant six bulbs.
X
=
Pr
: Question:
What is the probability that at least three bulbs will mature?
Since the probability of (i) at least three bulbs maturing
and
(ii) the probability of none or one or two maturing must add up to one (meaning certainty that either outcome (i) or outcome (ii) will occur), then the probability we require is given by
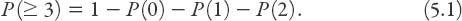
In order to proceed we need to introduce the concept of
combinations
,
n
C
r
, which represents the number of ways of choosing
r
items from a total of
n
(without regard to order). This is defined as

where for a positive integer
n
, for example, 5, 5! = 5 × 4 × 3 × 2 × 1 = 120. Furthermore, by definition, 0! = 1. Now
P
(
r
) is the probability that only
r
events will occur, and is given by the number of ways the event can occur, multiplied by the probability that
r
events do occur and (
n
−
r
) do not. Thus
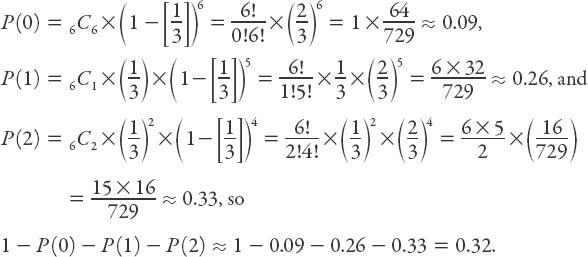
Or just under one third. Go for it, Felix!
According to Richard F. Burton [
12
], an expert in earthworms (and a contemporary of Charles Darwin) estimated that in a typical field there are about 133,000 earthworms per hectare. (A hectare is a square hectometer; a hectometer is 100 meters, so you’ll be delighted to know that we’re back with the metric system.)
X
=
N
: Question
: What is this figure in worms per square meter?
Clearly, a square hectometer is 10
4
sq m, so the only thing we need to do is divide by this number to get about 13 worms per square yard. Does that sound about right? Of course, it depends very much on the kind of soil, and we don’t worry about the 0.3 earthworm (unless it ends up in our apple [see
Chapter 4
]).
While we’re on the subject of slimy things, consider this. A certain species of slug is 80% water by weight. Suppose that it loses a quarter of this water by evaporation.
X
=
W
: Question
: What is its new percentage of water by weight?
If
W
and
W
new
are the weights of the slug “before and after,” so to speak, then in each case the weight can be distributed as the sum of the water content and the rest, that is,
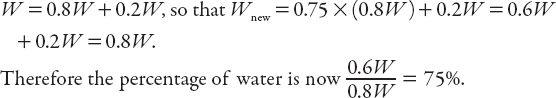
This is a little like the watermelon problem, isn’t it? Don’t confuse the two when eating, though. Do you recall the quote (from St. John of Patmos) about leaves on a tree? Let’s set up a simple framework for estimating the number of leaves on any tree or bush.
X
=
N
: Question:
How many leaves are on that laurel bush in my back yard?
I’ll approximate my smallish bush by a sphere of radius half a meter, so that’s a surface area (4
π
times radius squared) of about 3 m
2
. Now the leaves does not “continuously” cover the surface, but then again, there are leaves throughout much of the bush, not just on the outer “canopy,” so I’ll simplify this problem crudely by just assuming a continuous outer surface composed of leaves about 1 cm square, that is, of area 1 cm
2
= 10
−4
m
2
. Dividing 3 m
2
by this quantity gives us about
N
≈ 3 × 10
4
leaves.
Doubling the diameter of the bush to make it a small tree would quadruple the area, but the area of the individual leaves would probably be larger (depending on the type of tree), so for a yew tree, say, with typical leaf area about 4 cm
2
, these two effects would essentially cancel each other out, giving us a figure again of about 30,000 leaves, accurate to within a factor of two or three, I suspect.
Exercise:
Estimate the number of leaves on that really big tree in your neighborhood. And when you’ve done that, estimate the total length of the tree; that is, the trunk plus all the branches and twigs.
SUMMER IN THE CITY

Question:
How many squirrels live in Central Park?
Central Park in New York City runs from 59th Street to 110th Street [
6
]. At 20 blocks per mile, this is 2.5 miles. Central Park is long and narrow, so we will estimate its width at about 0.5 mile. This gives an area of about 1 square mile or about 2 square kilometers.
It’s difficult to estimate the number of squirrels in that large an area, so let’s break it down and think of the area of an (American) football field (about 50 yards × 100 yards). There will be more than 1 and fewer than 1000 squirrels living there, so we choose the number geometrically between 1 and 1000, or 30 (using the Goldilocks principle again).
This is where the metric system comes in handy. One kilometer (1000 m or about 1100 yards; we’ll round down to 1000 yards) is the length of ten football fields and the width of twenty. This means that there are 200 football fields in a square kilometer. Now the number of squirrels in Central Park is about
N
= (2 km
2
) × (200 football fields/(km
2
)) × (30 squirrels/football field) = 12,000 ≈ 10
4
. That’s enough squirrels for even the most ambitious dog to chase!