X and the City: Modeling Aspects of Urban Life (18 page)

Such local climate enhancement has several consequences, some of which are positive (or at least appear to be). For example, there may be a diminution of snowfall and reduced winter season in the city. This induces an earlier spring, other species of birds and insects may take up residence, and longer-lasting higher temperature heat waves can occur in summer (quite apart from any effects of larger scale climate change). This in turn means that less domestic heating may be required in the winter months, but more air-conditioning in the summer. The effects of an urban-industrial complex on weather generally are
harder to quantify, though stronger convective updrafts (and hence intensity of precipitation and storms) are to be expected downwind from urban areas. According to one report (Atkinson 1968), there has been a steadily increasing frequency of thunderstorm activity near London as it has grown in size. In U.S. cities, the incidence of thunderstorms is 10–42% greater than in rural areas, rainfall is 9–27% greater and hailstorms occur more frequently, by an enormous range: 67–430%.

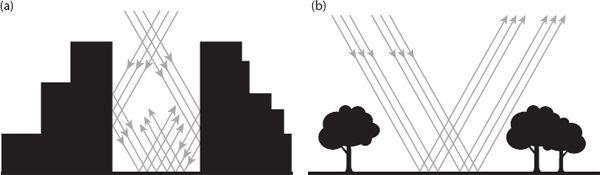
Figure 6.4. (a) Vertical surfaces tend to reflect solar radiation toward the ground and other vertical surfaces (thus trapping it), especially when the sun’s elevation is moderately high. (b) There being fewer vertical surfaces in the countryside, solar radiation tends to be reflected skyward. Redrawn from Lowry (1967).

If the air temperature were to be recorded as we move across the countryside toward a city, the rural/urban boundary will typically exhibit a sharp rise—a “cliff”—followed by a slower rate of increase (or even a plateau) until a more pronounced “peak” appears over the city center. If the temperature difference between the city and surrounding countryside at any given time is denoted by Δ
T
, the average annual value for Δ
T
ranges from 0.6 to 1.8°C. Of course, the detailed temperature profile as a function of position will vary depending on the time of day, but generally this is a typical shape: a warm “island” surrounded by a cooler “sea.” Obviously the presence of parks and other open areas, lakes, and commercial, industrial and heavily populated areas will modify this profile on a smaller spatial scale. The difference Δ
T
between the maximum urban temperature and the background rural temperature is called the
urban heat island intensity
. Not surprisingly, this exhibits a diurnal variation; it is at a maximum a few hours after sunset, and a minimum around the middle of the day. In some cases at midday the city is cooler than its environs, that is, Δ
T
< 0.

To see why this might be so, note that near midday the sunlight strikes both country and city environs quite directly, so Δ
T
can be small, even negative, possibly because of the slight cooling effect of shadows cast by tall buildings, even with the sun high overhead. As the day wears on and the sun gets lower, the solar radiation strikes the countryside at progressively lower angles, and much is accordingly reflected. However, even though the shadows cast by tall buildings in the city are longer than at midday, the sides facing the sun obviously intercept sunlight quite directly, contributing to an increase in temperature, just as in the hours well before noon, and Δ
T
increases once more.

Cities contribute to the “roughness” of the urban landscape, not unlike the effect of woods and rocky terrain in rural areas. Tall buildings provide considerable “drag” on the air flowing over and around them, and consequently tend to reduce the average wind speed compared with rural areas, though they create more turbulence (see
Chapter 3
). It has been found that for light winds,
wind speeds are greater in inner-city regions than outside, but this effect is reversed when the winds are strong. A further effect is that after sunset, when Δ
T
is largest, “country breezes”—inflows of cool air toward the higher temperature regions—are produced. Unfortunately, such breezes transport pollutants into the city center, and this is especially problematical during periods of smog.

Question:
Why is Δ
T
largest following sunset?

This is because of the difference between the rural and urban cooling rates. The countryside cools faster than the city during this period, at least for a few hours, and then the rates tend to be about the same, and Δ
T
is approximately constant until after sunrise, when it decreases even more as the rural area heats up faster than the city. Again, however, this behavior is affected by changes in the prevailing weather: wind speed, cloud cover, rainfall, and so on. Δ
T
is greatest for weak winds and cloudless skies; clouds, for example, tend to reduce losses by radiation. If there is no cloud cover, one study found that near sunset Δ
T
∝
w
^−1/2
, where
w
is the regional wind speed at a height of ten meters (see equation (6.7)).

Question:
Does Δ
T
depend on the population size?

This has a short answer: yes. For a population
N
, in the study mentioned above (including the effect of wind speed), it was found that

though other studies suggest that the data are best described by a logarithmic dependence of Δ
T
on log
₁₀
N
. While every equation (even an approximate one) tells a story, equation (6.7) doesn’t tell us much! Δ
T
is weakly dependent on the size of the population; according to this expression, for a given wind speed
w
a population increase by a factor of sixteen will only double Δ
T
! And if there is no wind? Clearly, the equation is not valid in this case; it is an empirical result based on the available data and valid only for ranges of
N
and
w
.

Exercise:
“Play” with suitably modified graphs of
N
^1/4
and log
₁₀
N
to see why data might be reasonably well fitted by either graph.

The reader will have noted that there is not much mathematics thus far in this subsection. As one might imagine, the scientific papers on this topic are heavily data-driven. While this is not in the least surprising, one consequence is that it is not always a simple task to extract a straightforward underlying mathematical model for the subject. However, for the reader who wishes to read a mathematically more sophisticated model of convection effects associated with urban heat islands, the paper by Olfe and Lee (1971) is well worth examining. Indeed, the interested reader is encouraged to consult the other articles listed in the references for some of the background to the research in this field.

To give just a “taste” of the paper by Olfe and Lee, one of the governing equations will be pulled out of the air, so to speak. Generally, I don’t like to do this, because everyone has the right to see where the equations come from, but in this case the derivation would take us too far afield. The model is two-dimensional (that is, there is no
y-
dependence), with
x
and
z
being the horizontal and vertical axes; the dependent variable
θ
is essentially the quantity Δ
T
above, assumed to be small enough to neglect its square and higher powers. The parameter
γ
depends on several constants including gravity and air flow speed, and is related to the Reynolds number discussed in
Chapter 3
. The non-dimensional equation for
θ
(
x
,
z
) is

The basic method is to seek elementary solutions of the form

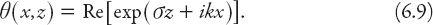
where “Re” means that the real part of the complex function is taken, and
k
is a real quantity On substituting this into equation (6.8) the following complex biquadratic polynomial is obtained:

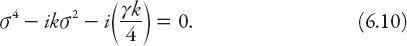
There are four solutions to this equation, namely,