X and the City: Modeling Aspects of Urban Life (88 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

From the earlier discussion we can identify
δV
, the relative difference in speeds, as
v
0
and the difference in orbital radii,
δa
, as the impact parameter
b
. Using equation (A12.7) in (A12.5) we obtain (in the current notation)
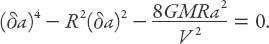
The positive real root of this biquadratic equation is
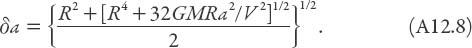
In performing these calculations I found it simplest to write the term
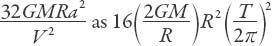
since
a/V
=
T
/2
π
, where
T
is the period of the Earth’s orbit in seconds. We have already calculated the quantity 2
GM
/
R
from equation (A12.6). The result is
δa
≈ 8.45 × 10
5
km (
δa
≈ 5.63 × 10
−3
A.U.). In terms of the Earth’s equatorial radius
R
≈ 6.38 × 10
3
km, this is about 132 Earth radii, or approximately 2.2 times the Earth-moon semi-major axis.
From equation (A12.7) we find that the corresponding difference in orbital speed |
δV
| ≈ 0.085 km/s.
Exercise:
Show from equations (A12.2) and (A12.5) that, for a grazing collision,
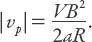
This shows that the perigee speed is quite sensitive to the impact parameter, varying as its square. Using this result we calculate the impact speed at a grazing collision to be ≈11.1 km/s, just a tiny bit less than the escape speed from the Earth. Since we have shown that the Earth sweeps out a toroidal volume of radius approximately 0.056 A.U. in its path around the sun, it can be thought of as a giant vacuum cleaner with CCS (132)
2
≈ 1.74 × 10
4
times that of the Earth’s GCS. Therefore any object moving in a circular orbit with radius between 0.9944 A.U. and 1.0056 A.U. will collide with (be captured by) the Earth. That’s some vacuum cleaner!
[
1
] Batty, M. and Longley, P. (1994).
Fractal Cities
. Academic Press, San Diego, CA.
[
2
] Polya, G. (1954).
Mathematics and Plausible Reasoning. I. Induction and Analogy in Mathematics
. Princeton University Press, Princeton, NJ.
[
3
] Hern, W.M. (2008). “Urban malignancy: similarity in the fractal dimensions of urban morphology and malignant neoplasms.”
International Journal of Anthropology
23, 1–19.
[
4
] See Adam (2006) for a slightly different version of the Princess Dido story.
[
5
] Barshinger, R. (1992). “How not to land at Lake Tahoe!”
American Mathematical Monthly
99, 453–455.
[
6
] Taxi rides, squirrels, and light bulbs: I am grateful to my friend, colleague, and co-author Larry Weinstein, an NYC boy, for his insights into city life; I have drawn on his expertise for these questions.
[
7
] Weinstein, L. and Adam, J.A. (2008).
Guesstimation: Solving the World’s Problems on the Back of a Cocktail Napkin
. Princeton University Press, Princeton, NJ.
[
8
] Eastaway, R. and Wyndham, J. (1999).
Why do Buses Come in Threes? The Hidden Mathematics of Everyday Life
. Wiley, London.
[
9
] Skyscrapers and harmonic motion: see
http://www.cpo.com/pdf/tpst_pfc%20ch19%20connections.pdf
.
[
10
] Burghes, D., Galbraith, P., Price, N. and Sherlock, A. (1996).
Mathematical Modelling
. Prentice-Hall, Hempstead, Hertfordshire.
[
11
] Barnes, G. (1990). “Food, eating, and mathematical scaling.”
Physics Teacher
28, 614–615.
[
12
] Burton, R.F. (1998).
Biology by Numbers
. Cambridge University Press, Cambridge.
[
13
] Edwards, D. and Hamson, M. (1989).
Guide to Mathematical Modelling
. CRC Press, Boca Raton, FL.
[
14
] Lowson, M.V. (2004). “Idealised models for public transport systems.”
International Journal of Transport Management
2, 135–147.
[
15
] Lowson, M.V. (1999). “Personal public transport.”
Proceedings of the Institution of Civil Engineers: Transportation
135, 139–151.
[
16
] Mahajan, S. (2010).
Street-Fighting Mathematics: The Art of Educated Guessing and Opportunistic Problem Solving
, MIT Press, Cambridge, MA.
[
17
] Seifert, H.S. (1962). “The stop-light dilemma.”
American Journal of Physics
30, 216–218.
[
18
] Chapman, S. (1942). “Should one stop or turn in order to avoid an automobile collision?”
American Journal of Physics
10, 22–27.
[
19
] Ashdon, W.D. (1966).
The Theory of Road Traffic Flow
. Methuen, London.
[
20
] Smeed, R.J. (1961).
The Traffic Problem in Towns
. Manchester Statistical Society, Manchester, England.
[21] Smeed, R.J. (1963). “The road space required for traffic in towns.”
Town Planning Review
33, 270–292.
[22] Smeed, R.J. (1963). “Road development in urban areas.”
Journal of the Institute of Highway Engineers
10, 5–26.
[23] Smeed, R.J. (1965). “A theoretical model for commuter traffic in towns.”
Journal of the Institute of Mathematics and its Applications
1, 208–225.
[24] Smeed, R.J. (1967). “The road capacity of city centers.”
Highway Research Record
169, 22–29.
[
25
] Smeed, R.J. (1968). “Traffic studies and urban congestion.”
Journal of Transport Economics and Policy
2, 33–70.
[26] Smeed, R.J. (1970). “The capacity of urban road networks.”
Proceedings of the Australian Road Research Board
5, 10–28.
[
27
] Smeed, R.J. (1977). “Traffic in a linear town.”
Proceedings of the 7th International Symposium on Transportation and Traffic Theory
.
[
28
] von Foerster, H., Mora, P.M., and Amiot, L.W. (1960). “Doomsday: Friday 13 November, A.D. 2026.”
Science
132, 1291–1295.
[
29
] Johansen, A. and Sornette, D. (2001). “Finite-time singularity in the dynamics of the world population, economic and financial indices.”
Physica A
294, 465–502.
[
30
] Bracken, A.J., and Tuckwell, H.C. (1992). “Simple mathematical models for urban growth.”
Proceedings of the Royal Society of London A
438, 171–181.
[
31
] Zipf, G.K. (1949).
Human Behavior and the Principle of Least Effort
. Harvard University Press, Cambridge, MA.
[
32
] Bettencourt, L.M.A., Helbing, J.L.D., Kühnert, C. and West, G.B. (2007). “Growth, innovation, scaling, and the pace of life in cities.”
Proceedings of the National Academy of Sciences of the USA
104, 7301–7306; also Bettencourt, L.M.A., Lobo, J. and West, G.B. (2008). “Why are large cities faster? Universal scaling and self-similarity in urban organization and dynamics.”
European Physical Journal B
63, 285–293.
[
33
] Ide, K., and Sornette, D. (2002). “Oscillatory finite-time singularities in finance, population and rupture.”
Physica A
307, 63–106.
[
34
] Bosanquet, C.H., and Pearson, J.L. (1936). “The spread of smoke and gases from chimneys.”
Transactions of the Faraday Society
32, 1249–1263.
[
35
]
http://www.ias.ac.in/initiat/sci_ed/resources/chemistry/LightScat.pdf
.
[
36
] Lynch, D., and Livingston, W. (2010).
Color and Light in Nature
. 2nd ed., reprint. Thule Scientific, Topanga, CA; p.26.
[
38
] Minnaert, M. (1954).
The Nature of Light and Colour in the Open Air
. Dover, New York. (German edition, 1993,
Light and Color in the Outdoors
, Springer-Verlag, Berlin.)
[
39
] See website by Christian Fenn, “Rainbows in diverging light.”
http://www.meteoros.de/rainbow/rbdive_1.htm
.
[
40
]
http://quirkynyc.com/2010/05/ahoy-lighthouses-litter-new-york-city/
.