X and the City: Modeling Aspects of Urban Life (85 page)
Read X and the City: Modeling Aspects of Urban Life Online
Authors: John A. Adam

And so in the usual limit, equation (A10.7) is generalized slightly to become

RAINBOW/HALO DETAILS
My heart leaps up when I behold a rainbow in the sky
—William Wordsworth
In
Chapter 22
a contrast was drawn between some meteorological optical effects—rainbows and some ice crystal halos—observed during the day, from those potentially observable from nearby light sources at night. This Appendix summarizes some of the salient features of rainbows and one of the common ice crystal halos.
So what is a rainbow, and what causes it? A rainbow is sunlight, displaced by reflection and dispersed by refraction in raindrops, seen by an observer with his or her back to the sun. The primary rainbow, which is the lower and brighter of two that may be seen, is formed from two refractions and one reflection in myriads of raindrops (see
Figure A11.1
). It can be seen and photographed, but it is not located at a specific place, only in a particular set of directions. Obviously the raindrops causing it are located in a specific region in front of the observer. The path for the secondary rainbow is similar, but involves one more internal reflection. In principle, an unlimited number of higher-order rainbows exist from a single drop, but light loss at each reflection limits the number of visible rainbows to two. Claims have been made concerning observations of a tertiary bow (and even a quaternary bow), however, such a bow would occur around the sun, and be very difficult to observe, quite apart from its intrinsic faintness. Nevertheless, in 2011, significant photographic evidence for such bows was published in a reputable scientific journal (see Groβmann et al. (2011) and Theusner (2011)); it will be exciting to see what further research is carried out in this area.
Returning to the primary bow, note that while each drop produces its individual primary rainbow, what is seen by an observer is the cumulative set of images from myriads of drops, some contributing to the red region of the bow, others to the orange, yellow, green, and so forth. Although each drop is falling, there are numerous drops to replace each one as it falls through a particular location, and so the rainbow, for the period that it lasts, is for each observer effectively a continuum of colors produced by a near-continuum of drops.
Let’s start with an examination of the basic geometry for a light ray entering a spherical droplet. From
Figure A11.1
note that after two refractions and one reflection the light ray shown contributing to the rainbow has undergone a total deviation of
D
(
i
) radians, where

in terms of the angles of incidence (
i
) and refraction (
r
), respectively. The latter is a function of the former, this relationship being expressed in terms of Snell’s law of refraction,

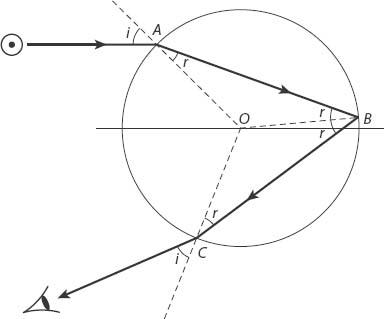
Figure A11.1. Ray path inside a spherical drop in the formation of a primary rainbow from sunlight.
where
n
is the
relative index of refraction
(of water, in this case). This relative index is defined as

Since the speed of light in air is almost that “in vacuo,” we will refer to
n
for simplicity as the refractive index; its generic value for water is
n
≈ 4/3, but it does depend slightly on wavelength (this is the phenomenon of dispersion, and without it we would only have bright “white bows”!)
How does the deviation angle
D
vary with the angle of incidence
i
? Note that for rays that enter the sphere along the axis of symmetry and are reflected from the back surface,
D
(0) =
π
. The classic “rainbow problem” is to find whether there are maxima or minima in this deviation angle as a function of the angle
i
. On differentiating equation (A11.1) with respect to
i
, and using equation (A11.2), it is found that
D
′(
i
) = 0 when

for
n
= 4/3, on converting to degrees of arc. This means that
D
is stationary at
i
=
i
c
. Physically, this corresponds to a concentration of deviated rays in a small angular region about

It can be shown that
D
″(
i
c
) > 0, so that the deflection
D
(
i
c
) is a minimum (in fact it is a global minimum in (0,
π
/2) because
D
″(
i
c
) > 0). This minimum angle of deviation is often referred to as the
rainbow angle
. Its supplement 180° −
D
(
i
c
) ≈ 42° is the semi-angle of the rainbow “cone” formed with apex at the observer’s eye, the axis being the line joining the eye to the shadow of her head (the antisolar point).
A comment about the color dispersion in a rainbow is in order. While it is not standardized to the satisfaction of everyone, the visible part of the electromagnetic spectrum extends from the “red” end (700–647 nm, or 0.700
μ
–0.647
μ
, etc.) to the “violet” end (424–400 nm), a nanometer (nm) being 10
−9
m. For red light of wavelength
λ
≈ 656 nm, the refractive index
n
≈ 1.3318, whereas for violet light of wavelength
λ
≈ 405 nm, the refractive index
n
≈ 1.3435, a slight but very significant difference! All that has to be done is the calculation of
i
c
and
D
(
i
c
) for these two extremes of the visible spectrum, and the difference computed. Then voilà! We have the angular width of the primary rainbow. In fact since
D
(
i
c
) ≈ 137.8° and 139.4° for the red and violet ends, respectively, the angular width is Δ
D
≈ 1.6°, or about three full moon angular widths.
There is also a secondary rainbow that is frequently visible along with the primary bow as a result of an extra reflection inside the raindrops. As a result it is the fainter of the two, slightly wider, and about 9 degrees “higher” in the sky than the primary bow.
What about the common halo mentioned above? Have you ever noticed a circular ring around the sun (or, for that matter, the moon) when the sky is clear except for wispy thin cirrus clouds in the vicinity of the sun? I read on a now-defunct website that such beautiful displays, known as ice crystal halos, can be seen on average twice a week in Europe and parts of the United States, and certainly my own experience is not terribly different, though I would estimate that I notice them about three times a month on average. The “radius” of a ring around the sun or moon is naturally expressed in terms of degrees of arc, subtended at the observer’s eye by the apparent radius, just as for the rainbow. The most frequently visible one is the 22° circular halo, followed by parhelia (or
sundogs
, colored “splotches” of light on one side or other of the sun, and commonly both). In my own rather limited experience, the sundogs are as common as the halo if not more so, at least as I walk to work in southeastern Virginia. These are found at the same altitude as the sun, close to (but just beyond) the 22° halo. A convenient and literal “rule of thumb” is that the outstretched hand at arm’s length subtends about the same angle, so that if one’s thumb covers the sun, one’s little finger extends to about the 22° halo (or the sundog). There are
many
other types of ice crystal displays; for more information consult the encyclopedic and highly regarded website by atmospheric optics expert Les Cowley [
46
].